Морская и океаническая вода в сине-зеленой области обладает очень малым показателем поглощения (α~10-4–10-3 м-1). Его определение является сложной технической задачей, в первую очередь из-за того, что она обладает значительным показателем рассеяния (ks~10-2-10-1 м-1). Классические методики определения поглощения основаны на измерении интенсивностей падающего, прошедшего и рассеянного излучения и поэтому дают значительную ошибку (100–500 %). В работе [1] изложено применение метода «тепловой линзы» для стабилизации мощности излучения лазера. Он основан на явлении самодефокусировки лазерного пучка при прохождении через исследуемую среду. В [2] описывается использование этого метода для нахождения показателя поглощения слабопоглощающих жидкостей. Там же рассмотрена экспериментальная установка для его реализации, показано, что относительное изменение мощности излучения после диафрагмы в первом приближении прямо пропорционально показателю поглощения среды. Оценен динамический диапазон и чувствительность метода. Также было сделано предположение, что данный способ может использоваться для исследования сред, в которых показатель рассеяния значительно превышает показатель поглощения.
Цель данной работы – изучить возможность применения метода «тепловой линзы» для определения малого показателя поглощения сильно рассеивающей среды и исследовать зависимость точности определения поглощения от показателя рассеяния для разных размеров рассеивающих сфер.
Рассеяние в среде с однородными частицами
Диаграмма рассеяние света одиночной частицей зависит от ее размера и формы.
Пусть частица освещается плоской волной бесконечной протяженности, идущей в направлении оси z.
Еi = Е0exp[i(kz-ωt)]. (1)
Рассеянная волна на большом расстоянии является сферической волной с амплитудой, зависящей от угла и обратно пропорциональной расстоянию r.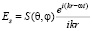 
. Амплитудная функция S(θ, φ) комплексная и может быть записана в виде S(θ, φ) = s∙exp[iφ(θ)], где s положительно а φ вещественно, причем φ-π/2 < 0, т.е. фаза рассеянной волны запаздывает относительно падающей. Так как интенсивность волны пропорциональна квадрату амплитуды, то интенсивность находится как
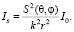(2)
Для направления вперед (θ = 0) из соображений непрерывности получаем S(0) = s(0)exp[i∙φ(0)].
В нашем случае свет, рассеянный на большие углы, быстро выходит из области тепловой линзы, что приводит только к экспоненциальному уменьшению его интенсивности пучка. Поэтому для света, рассеянного вперед (под малыми углами), можно использовать параксиальное приближение r = z + (x2 + y2)/2z. Общая амплитуда волны определяется суперпозицией рассеянной и падающей волн.
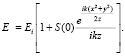(3)
В этом выражении второе слагаемое много меньше 1, поэтому полная интенсивность света может быть найдена как
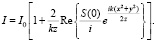(4)
Зависимость от формы частицы незначительна [3] и ее в первом приближении можно не учитывать. Поэтому мы будем рассматривать рассеяние на однородных шарах с показателем преломления, отличным от показателя преломления среды.
Для сферической рассеивателя зависимости от φ не будет. Кроме этого исчезает зависимость от поляризации света и матричные уравнения переходят в скалярные
Is = |S(θ)|2∙I0. (5)
Основной вклад в рассеяние на небольшой угол вносит дифракция света. Основная интенсивность светового потока (98 %) сосредоточена в угле определяющим первый дифракционный минимум. В случае сферы диаметром d – угол θ = (1,22λ)/(n2d), λ – длина волны, n2 – показатель преломления среды. Для шаров с размером d >> λ и гладкой поверхностью нужно учитывать рефракцию и отражение света. Это приводит к появлению дополнительных поправочных членов в конечном выражении.
Если диаметр шара мал и относительный показатель преломления невелик (4πd(n21-1)/λ<<1, то можно найти S(θ) по формулам теории Релея-Ганса:
S(θ) = ik3∙α∙exp(iφ)∙cos(θ); (6)
α = (n21 – 1)d3/12, k = 2π/λ, φ – сдвиг фазы, зависящий от θ. При этом каждый элемент объема дает релеевское рассеяние независимо от других элементов объема. Волны, рассеянные в данном направлении разными элементами, интерферируют. Расчеты диаграммы направленности проводились численными методами на основании классических формул, рекомендуемых для практического применения в работе [4]. Результаты расчета для некоторых случаев представлены на рис. 1.
Прохождение света через облако частиц
Когерентная составляющая лазерного пучка, проходя через облако частиц экспоненциально убывает
I(z) = I0∙exp(-ks∙z), (7)
ks – показатель рассеяния света, ks = σn, σ – эффективное сечение рассеяния, n – концентрация частиц. Рассеянный свет может повлиять на конечный сигнал, если он выйдет незначительно за пределы области взаимодействия (θ = 0,5˚–1˚) [5]. Практически такие углы соответствуют рассеянию на рассеивателях больших размеров (d >> λ). Рассеяние можно считать однократным, если выполняется условие σN < S, N – общее число частиц, S – освещаемая в образце площадь. Для среды длиной L это условие легко свести к виду σ∙n∙L < 1. Используя (7) получаем макроусловие для однократного рассеяния. Ему соответствует ослабление интенсивности прошедшего света не более чем в 2,7 раза (I0/I < 2,7).
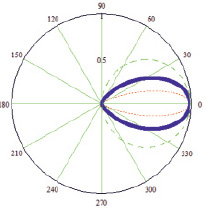
Рис. 1. Диаграмма направленности света (длина волны λ = 0,65 мкм), рассеянного вперед одиночными сферическими объектами разных размеров (относительный показатель преломления сферы n21 = 1,15): 1 – диаметр сферы 3 мкм (внешняя пунктирная линия), 2 – диаметр сферы 1,2 мкм (толстая линия), 3 – диаметр сферы 0,5 мкм (внутренняя пунктирная линия)
Использование сферических частиц, для которых вероятность рассеяния неполяризованного света не зависит от азимутального угла φ, позволяет оценить средний угол для m случаев рассеяния как θm ≈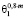 
, θ1 – средний угол однократного рассеяния. Таким образом, при многократном рассеянии вероятность выхода излучения за пределы области «тепловой линзы» выше, чем при однократном.
Схема эксперимента
Лазерное излучение с длиной волны λ ≈ 650 нм и мощностью Р = 10 мВт проходило через коллиматор (рис.2), конструктивно объединенный с электрооптическим модулятором света, который создавал импульсы длительностью 0,01–50 мс. Шейка каустики формировалась линзой с фокусным расстоянием F = 25 см.
Рис. 2. Экспериментальная установка: 1 – полупроводниковый лазер OMEGA LASER PEN RP50, 2 – коллиматор с электрооптическим модулятором света, 3 – фокусирующая линза, 4 исследуемый образец, 5 – диафрагма, вырезающая центральную часть пучка, 6 – фотодиод, 7 – цифровой вольтметр
Диаметр пучка на линзе составил d = 3 мм. Первоначально использовалась кювета длиной 1 см. Используя методику расчета комплексного параметра пучка q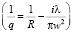 
(R – радиус кривизны волнового фронта, w = d/2), легко получить положение и размер перетяжки за линзой.
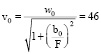мкм,
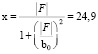см.
Кювета с образцом помещалась таким образом, чтобы ее середина находилась на расстоянии, равном конфокальному параметру (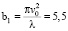
мм, за плоскостью максимальной фокусировки. На таком расстоянии изменение расходимости пучка будет наибольшим. В последующих экспериментах длина кюветы менялась от 3 до 40 мм. В качестве рассеивателей использовалась водная гидрозоль с калиброванными полистирольными шариками (для λ = 650 нм показатель преломления n = 1,57, относительный показатель преломления n21 = 1,18) диаметром d = 0,5 мкм, 1,2 мкм и 3 мкм.
Экспериментальные результаты
На данной установке были проведены измерения зависимости изменения интенсивности в центре лазерного пучка из-за самодефокусировки (сигнала «тепловой линзы») от показателя рассеяния среды для рассеивающих сфер диаметром 0,5 мкм, 1,2 мкм и 3 мкм. Результаты измерений и расчеты для данных рассеивателей с учетом их диаграмм направленностей приведены на рис. 3. Для шариков диаметром 0,5 мкм результаты измерений с вероятностью 99 % ложатся на экспоненциальную зависимость ослабления интенсивности (верхняя штриховая линия соответствует рассчитанной зависимости). То есть рассеяние на таких объектах практически не влияет на определение показателя поглощения вещества методом «тепловой линзы».
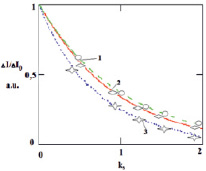
Рис. 3. Зависимость изменения интенсивности света в центре лазерного пучка от показателя рассеяния среды для различных размеров рассеивающих сфер: 1) d = 0,5 мкм, 2) d = 1,2 мкм, 3) d = 3 мкм
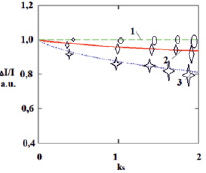
Рис. 4. Относительное изменение интенсивности света в центре лазерного пучка в зависимости от показателя рассеяния среды для различных размеров рассеивающих сфер: 1) d = 0,5 мкм, 2) d = 1,2 мкм, 3) d = 3 мкм.
На рис. 4 это выглядит как неизменное значение относительного изменения интенсивности света в центре пучка. В случае сферических рассеивателей диаметром 1,2 мкм сигнал уменьшается несколько сильнее (средняя сплошная линия). Относительный сигнал (фактически точность измерения показателя поглощения), как видно из рис. 4, падает, но незначительно. Изменение сравнимо с погрешностью. Для сфер диаметром 3 мкм получено самое большое изменение сигнала с ростом показателя рассеяния (нижняя пунктирная кривая). Для показателя рассеяния ks = 2 относительный сигнал (точность измерения) уменьшился более чем на 20 %. Как следует из расчетов, для более крупных рассеивателей погрешности измерения будут возрастать.
Заключение
В работе изучена возможность применения метода «тепловой линзы» для определения малого показателя поглощения сильно рассеивающей среды, исследована зависимость изменения интенсивности в центре лазерного пучка из-за самодефокусировки при прохождении через слабо поглощающую среду (сигнала «тепловой линзы») от показателя рассеяния и найдена зависимость точности определения показателя поглощения от показателя рассеяния для разных размеров рассеивающих сфер. Экспериментальные значения показали хорошее совпадение с расчетами. Частицы малого размера (порядка длины волны света) рассеивают излучение на большие углы, что приводит только к уменьшению полной мощности пучка. Для такого случая эта методика может быть применена для определения поглощения даже сред с малым поглощением и значительным рассеянием (показатель поглощения α ~ 10-3 м-1, показатель рассеяния ks ~ 102 м-1). Для частиц большого размера (d ≥ 3 мкм) погрешность метода может составить 5–10 % для ks ~ 10 м-1 и 20–40 % для ks ~ 102 м-1.