В работах [1–3] рассматривается схема восстановления последовательности саморепродукций в случае голографической записи линейной решетки. Голограмма решетки записывалась по стандартной внеосевой схеме с использованием наклонного опорного пучка. Запись голограммы осуществлялась при условии, что расстояние между плоскостью записи и решеткой в точности была кратна некоторой фиксированной величине, называемой постоянной саморепродуцирования. Голограмма, восстановленная исходной опорной волной, формировала не только мнимое изображение решетки, но и последовательность ее саморепродукций [4–6]. При восстановлении голограммы решетки волной, сопряженной исходной опорной волне, восстанавливались действительные изображения решетки и последовательности саморепродукций. Основные выводы, которые делали авторы по результатам своих исследований, это то, что обязательным требованием для восстановления решетки и последовательности саморепродукций является точное соблюдение условия для расстояния между плоскостями голограммы решетки и самой решетки – расстояние должно быть кратным постоянной саморепродуцирования.
Целью данной работы является рассмотрение более общего случая записи голограммы линейной решетки, для которого расстояние между плоскостями объекта-решетки и голограммы берется абсолютно произвольно [7–9].
Саморепродуцирование в голографии
При записи пропускающих объектов, таких как линейная решетка, необходимость в использовании дополнительной, соосной объектной волне, опорной волны в схеме записи радужной голограммы отпадает. Особенностью пропускающих объектов является то, что в этом случае объектную волну можно рассматривать, как совокупность двух составляющих: дифрагированная и недифрагированная части. Недифрагированную часть можно рассматривать как соосную предметной волне опорную волну.
Схематично процесс записи голограммы периодического объекта – линейной одномерной решетки – представлен на рис. 1 [10–12].
Объект Р – его плоскость (x0, y0) – удален на расстояние z1 от параллельно расположенной плоскости фотопластинки (x, y). φ – угол, который образуют предметная волна и перпендикуляр к плоскости голограммы. Угол, который образуют опорная и объектная волны, также равен φ.
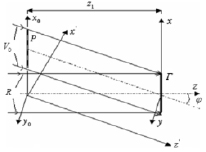
Рис. 1. Схема записи голограммы Г периодического объекта: Р – решетка;
R – опорная волна; V0 – объектная волна
Для схемы, соответствующей рис. 1, выражение для плоской волны, освещающей объект, имеет вид
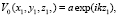(1)
где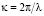 
– волновое число, λ – длина падающей волны, z1 – ось, соответствующая направлению распространения волны, а – амплитуда освещающей волны.
Окончательное выражение для поля за решеткой записывается в виде
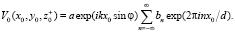(2)
Здесь d – период линейной решетки.
относительно
Выражение для поля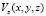 
в плоскости голограммы Г находится как приближение Френеля [13–15]:
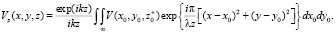(3)
Несложные расчеты дают
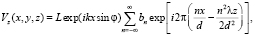(4)
где L – некоторый фиксированный множитель.
Плоская опорная волна распространяется вдоль оси z, т.е. на плоскость голограммы эта волна падает перпендикулярно:
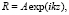(5)
здесь А – амплитуда опорной волны.
Пропускающий коэффициент одномерной линейной решетки можно рассматривать как сумму следующего вида
σ = σ0 + σn, (6)
где σ0 – фиксированная составляющая пропускающего коэффициента решетки, имеющая нулевую пространственную частоту, а σn – составляющая с ненулевой частотой. Объектное поле на удалении z от плоскости решетки имеет вид
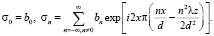(7)
Расчет поля для этого случая в районе плоскости голограммы дает соотношение следующего вида
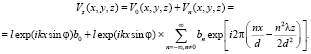(8)
Для распределения интенсивности поля вблизи плоскости голограммы получаем соотношение
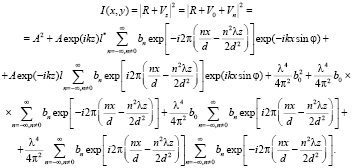(9)
Если осветить данную голограмму опорной волной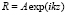 
, которая использовалась при записи, то она восстанавливает за голограммой три луча, представляющих собой дифракционные порядки, направление которых определяется значением угла φ между лучами распространения опорной и объектной волн (рис. 2). Рассмотрим +1-й порядок дифракции. Этот порядок соответствует распространению световой волны в направлении +θ перпендикуляра к плоскости голограммы и описывается соотношением
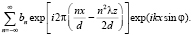(10)
В нулевом порядке дифракции мы можем наблюдать, по сути, то, что происходит при восстановлении голограммы Габора.
Совместное действие двух слагаемых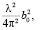 
и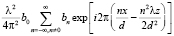 
равносильно формированию волны, которая как бы является результатом отражения от мнимого изображения объекта, расположенного на том же самом месте, где был расположен и сам объект при съемке.
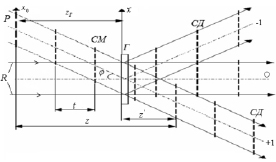
Рис. 2. Схема восстановления голограммы регулярного объекта: Р – мнимое изображение объекта; СМ – положения саморепродукций в мнимой области пространства; СД – положения саморепродукций в действительной области пространства; Г – голограмма
Перейдем к рассмотрению +1-го порядка дифракции. В соответствии с (10), из указанного соотношения легко получить выражение, описывающее изображение решетки, возникающее сразу за ней, если взять значение второго слагаемого в показателе экспоненты таким образом, чтоб оно было кратным 2p, т.е.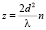 
,
где n = 0, 1, 2, 3, ... Соотношение, которое определяет положения саморепродукций: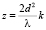 
, где k = l/2, l = 0, 1, 2, 3, ...
Здесь значения z в выражении (10) – это координаты, которые задаются вдоль оси, перпендикулярной к плоскости записанной решетки. Координаты плоскостей саморепродукции в +1 порядке дифракции можно записать в виде
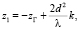(11)
здесь k = l, l = 0, 1, 2, 3, ...; –zГ – расстояние между восстановленным изображением и плоскостью голограммы; система координат z1, имеющая начало в плоскости голограммы.
Рассмотрим –1-й порядок дифракции. Подобно предыдущему случаю, координаты положений плоскостей саморепродукции в этом порядке дифракции также можно представить в виде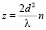 
,
(n = l/2, l = 0, 1, 2, 3, ...). Соотношение, определяющее положения плоскостей
саморепродукций:
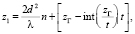(12)
здесь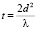 
– постоянная саморепродуцирования, n = l/2, (l = 0, 1, 2, 3, ...). Для координат, задающих положения плоскостей саморепродукции в нулевом порядке дифракции, получается соотношение, совпадающее с (12) в –1-м порядке дифракции:
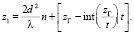
Выводы
1. Проведен теоретический анализ голографического процесса для периодического объекта типа линейной решетки.
2. Показано, что при восстановлении регулярного периодического объекта необходимо учитывать, что при восстановлении голограммы возникают не только изображения решетки, но и вся последовательность саморепродукций.
Анализ процесса восстановления при таком подходе показывает, что в этом случае в обоих порядках дифракции объекты захватывают как мнимое, так и действительное области пространства, т.е. деление на мнимое и действительное изображения теряет смысл. Оба изображения можно видеть одновременно в обоих порядках дифракции в случае восстановления исходной опорной волной или сопряженной ей.
3. Важной особенностью голографического процесса для регулярного объекта является то, что последовательность саморепродукций формируется также в и нулевом порядке дифракции, причем эта последовательность видна одновременно и как действительный объект, и как мнимый.