В работе [1] сформулирована концепция самодвижения тела в жидкости. Находящееся в жидкости тело совершает в ней самодвижение, если движение тела является следствием того, что тело отталкивается от жидкости. Самодвижение тела в жидкости происходит за счет взаимодействия между его границей и жидкостью (но не вследствие каких-либо воздействий на жидкость, которые могут осуществляться и в отсутствие в ней тела). Ввиду этого граница самодвижущегося тела является его движителем. Работа движителя при самодвижении соответствует тому, что на границе тела обеспечиваются условия, при которых выполняются уравнения самодвижения тела в жидкости.
Исследования, направленные на выявление закономерностей течения жидкости вокруг самодвижущихся тел, неизменно сохраняют актуальность. В работах [2, 3] выполнено моделирование течения жидкости в следе за телом; работы [4, 5] посвящены рассмотрению течения жидкости вокруг вращающегося тора. В основном интерес представляет движение вязкой жидкости. Задачи, касающиеся динамики вязкой жидкости, как правило, характеризуются повышенным уровнем сложности. Весомым дополнительным препятствием в их изучении является парадокс Стокса. Данный парадокс состоит в том, что решение задачи о плоском течении не ограниченной извне, покоящейся на бесконечности вязкой жидкости вокруг твердого цилиндрического тела, движущегося в ней с постоянной скоростью – равно как и решение эквивалентной задачи о стационарном обтекании твердого цилиндрического тела вязкой жидкостью – при малых значениях числа Рейнольдса, в приближении Стокса не существует.
Главной целью настоящей работы является установление связи между самодвижением твердого цилиндрического тела в вязкой жидкости и парадоксом Стокса.
В вязкой несжимаемой не ограниченной извне жидкости находится твердое тело Ξ – бесконечно длинный круговой цилиндр радиуса A. Тело Ξ покоится относительно инерциальной прямоугольной системы координат X, Y, Z. Жидкость на бесконечности движется с постоянной скоростью V∞ = {V∞, 0, 0} (V∞ > 0). Граница тела Ξ – цилиндрическая поверхность ΓΞ: X2 + Y2 = A2 (– ∞ < Z < ∞) – проницаема для жидкости. Течение жидкости является стационарным, плоским и симметричным относительно плоскости Y = 0. Тело Ξ может совершать (или не совершать) самодвижение в жидкости, обусловленное протеканием (втеканием и вытеканием) жидкости через поверхность ΓΞ. Самодвижение тела Ξ относительно жидкости на бесконечности происходит со скоростью – V∞ .
Пусть x = X/A; y = Y/A; z = Z/A; ex = {1, 0, 0}; ey = {0, 1, 0}; ez = {0, 0, 1}; r = xex + yey; r = |r|; er = r/r; θ – угол между векторами ex и er; eθ = ez×er; ξ – часть тела Ξ, «вписанная» между плоскостями Z = – H/2 и Z = H/2 (H > 0 – постоянная); h = H/A; Γξ – боковая поверхность тела ξ; V, ρ и ν – соответственно скорость, плотность и кинематический коэффициент вязкости жидкости; v = V/V∞ = vrer + vθeθ; P – давление в жидкости;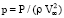 
; Re = AV∞/ν – число Рейнольдса; φ = φ(θ, Re) = 
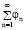cos nθ (φn = φn(Re)); S – поток импульса жидкости через поверхность Γξ в тело ξ (импульс, передаваемый жидкостью телу ξ в единицу времени); T – поток момента импульса жидкости относительно начала координат X, Y, Z через поверхность Γξ в тело ξ (момент импульса, передаваемый жидкостью телу ξ в единицу времени, относительно начала координат X, Y, Z);
; 
;
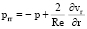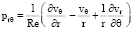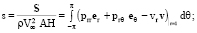
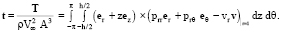
Определим следующую – полную – задачу
s = 0; (1)
t = 0 (2)
– уравнения самодвижения тела Ξ (тела ξ ) в жидкости;
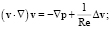(3)
∇•v = 0 (4)
– уравнения Навье – Стокса и неразрывности;
v = φer при r = 1; (5)
v → ex при r → ∞ (6)
– условия на твердой границе жидкости и на бесконечности.
Согласно (1), (2) имеем
f + g = 0, (7)
где
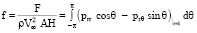(8)
(F – сила, действующая со стороны жидкости на тело ξ в направлении оси X);
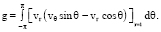
Тело Ξ является самодвижущимся (в жидкости) тогда и только тогда, когда выполняется уравнение (7).
Будем рассматривать задачу (3)–(7) при малых по сравнению с единицей значениях Re.
Предположим, что
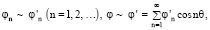
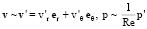при Re > 0. (9)
Согласно (8), (9) имеем
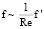при Re > 0. (10)
Здесь
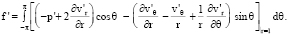(11)
Используя (3)–(7), (9), (10), получим
f' = 0 (12)
– уравнение самодвижения тела Ξ (тела ξ ) в жидкости в приближении Стокса;
Δv' = ∇p'; (13)
∇•v' = 0; (14)
v' = φ'er при r = 1; (15)
v' → ex при r → ∞ (16)
– задача о течении жидкости в приближении Стокса.
Пусть
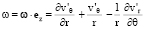(17)
(ω = ∇×v' – безразмерная завихренность жидкости в приближении Стокса).
Используя (13), (14), преобразуем формулу (11) к виду
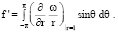(18)
В соответствии с (14)–(17) выполняются соотношения
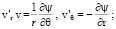(19)
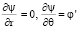при r = 1; (20)
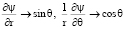при r → ∞; (21)
ΔΨ = –ω (22)
(Ψ – безразмерная функция тока жидкости в приближении Стокса).
Из (13) следует
Δω = 0. (23)
Решая уравнение (23), найдем
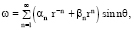(24)
где αn, βn – постоянные.
Используя (18), (24), получим
f' = –2πα1. (25)
Согласно (25) уравнение (12) выполняется, тело Ξ является самодвижущимся (в жидкости) тогда и только тогда, когда α1 = 0.
Обратимся к задаче (20), (22), (24). Решая данную задачу, принимая во внимание соотношение (25), найдем
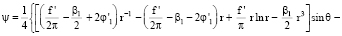
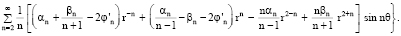(26)
Пусть тело Ξ не является самодвижущимся (уравнение самодвижения (12) не выполняется). Тогда функция ψ (определяемая формулой (26)) не удовлетворяет условиям (21) ни при каких значениях постоянных αm(m = 2,3,…), βn(n = 1,2,…) ввиду присутствия в правой части (26) слагаемого (4π)–1 f' r ln r sin θ, решение задачи (13)–(16) не существует.
Пусть тело Ξ является самодвижущимся (уравнение самодвижения (12) выполняется). Используя (21), (26), найдем
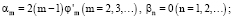
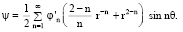(27)
Здесь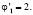 
Из (13), (19), (27) следует
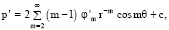(28)
где c – функция времени. Задача (13)–(16) имеет решение (19), (27), (28).
Таким образом, решение плоской задачи о стационарном обтекании не ограниченной извне вязкой жидкостью твердого цилиндрического тела, при малых значениях числа Рейнольдса (в приближении Стокса) существует – парадокс Стокса отсутствует – тогда и только тогда, когда обтекаемое жидкостью тело является самодвижущимся. Отметим, что данный результат получен ранее в работе [6] для твердого цилиндрического тела с движущейся границей.
Заключение
Выявление закономерностей совместного движения твердых тел и вязкой жидкости в различных гидромеханических условиях является одной из важнейших проблем механики жидкости. В связи с этим может представлять существенный интерес проведенное в данной работе рассмотрение, указывающее, в частности, на наличие нетривиального подхода, позволяющего обойти парадокс Стокса, избежать его возникновения. Изложенное в настоящей работе может использоваться в исследованиях в области механики жидкости, в том числе при поиске и изучении новых содержательных задач о плоских течениях вязкой жидкости вокруг твердых цилиндрических тел.