Гипотеза Римана, ученика Гаусса, об особенностях расположения нетривиальных нулей дзета-функции признана одной из самых интересных в ее разрешении математических задач [1]. О повышенном внимании к этой проблеме можно судить по компьютерному ее исследованию академиком Ю. Матиясевичем [2] и выступлению другого крупного математика М. Атьи [3]. В первом случае любопытна практика преобразования комплексной плоскости так, чтобы критическая полоса перешла в круг с кольцом, вблизи которого концентрируются нули аппроксимирующей функции. Во втором – не менее интересна физическая интерпретация математической задачи, поскольку в тексте появляются физические константы, что вызывает неоднозначную реакцию среди математиков.
В нашей статье, посвященной компьютерному исследованию в интернет-сети «Живая книга» с исполняемыми онлайн алгоритмами [4, 5], важна именно вторая интерпретация, поскольку исторические корни этой проблемы уходят к попыткам в XIV в. изучить физическое движение построением первых графиков перемещений и скоростей путников, которых сегодня можно представить 3D-анимацией. Наглядно можно представить также изменения в их перемещениях с учетом изменений, внесенные в формулы Эйлером и Риманом, позволяющие большему числу читателей понять смысл этих преобразований.
Целью данной работы является графическое построение средствами анимационной 3D-графики аттракторов динамических систем, описываемых рядом дзета-функции [1].
Большое внимание при выполнении этой работы было уделено исторической среде, давшей первую физическую трактовку дзета-функции, прозвучавшей в работах одного из первых иллюстраторов науки, изобретателя графиков, ученого и теолога Николая Орема.
По замыслу авторов работа, несмотря на ее ограниченный объем, должна охватывать не только текущие интерпретации, но и дать обзор возникновения взглядов.
История моделей путников
Первые модели движения, появившиеся в XIV в., концентрировали внимание на странности перемещений предметов в каюте движущегося корабля. Они происходили так, как если бы корабль стоял на месте. Это приводило к выводам, например, по отношению к Земле, которая уже тогда, благодаря измерениям до Солнца и Луны античной наукой, могла считаться подвижным кораблем среди них.
Логик Буридан исключал двойственность толкования тем, что по воле высших сил свершается только то, что приносит больше добра, а предположение о движении Земли никому не нужно (бесполезно). Его ученик, Николай Орем, строя график перемещения предмета точками, напоминающими вместе с осью времени отрезки пирога, овладел новым для тех времен методом абстракции. Он понял, что по вертикальной оси можно откладывать не только путь, но и скорость. В итоге он доказал, что равномерно устающий путник проходит одинаковый путь с путником, движущимся со средней скоростью, которая на графике скоростей, естественно, выглядит как средняя точка между начальной и конечной скоростями.
Для описания равномерного уставания годится гармонический ряд 1/n, описывающий все более короткие отрезки проходимого пути. Отсюда он вывел неожиданный для его современников вывод: путник, скорость которого падает до любой сколь угодно малой величины, пройдет любой по протяженности путь, поскольку всегда можно вычислить время равномерного движения. В теории дзета-функции эти параметры движения отвечают ее единственному полюсу. Это заключение, как видно, касается физической модели пути, оперирует физическими понятиями. Странность его только подчеркивалась тем, что если путник устает быстрее, например в виде 1/n2, то путь оказывается конечным.
Леонард Эйлер, который, находясь в петровской Академии, выступил собирателем различных математических и исторических фактов, был очень мощным вычислителем и установил длину пути, которую пройдет указанный путник, движущийся медленнее, – она оказалась пропорциональной квадрату числа π [1]. Что касается путника, который движется быстрее, проходя отрезки пути n, то еще в начале прошлого века зарождающийся в Индии талант Рамануджан описывал британскому профессору Харди эту ситуацию как анекдотическую, поскольку путник как будто бы проходил точку бесконечности и появлялся с противоположной стороны, не доходя до начала своего пути величины, обратной дюжине – 1/12.
Для Харди это тоже было потрясением, но иного характера, поскольку выходило, что молодой клерк, провинциал, самостоятельно вычислил значение очень абстрактной функции, созданной математическими талантами Орема, Эйлера и Римана. Ученик Гаусса Риман нашел специфический выход для описаний движения путников, движущихся быстрее путника Орема. Для этого нужно всего лишь только позволить им вполне безобидное действие – менять направление движения. Разумеется, бесконечный путь нельзя уложить вдоль сколь угодно петляющей нити, на то он и бесконечный. Но ведь петляние может стать однообразным и свестись к тому, к чему давно привыкли физики – к сколь угодно долго успокаивающимся колебаниям. В теории динамических систем, которая тогда еще только зарождалась, есть понятие реакции апериодической или колебательной системы. Статический коэффициент усиления ее отделяется от гармонических составляющих, позволяя судить о точке успокоения. Этим же способом пользуется продавец, смотря на стрелку пружинных весов.
Так получилось, что Эйлер, который всего лишь менял вещественные показатели степени усталости, но не менял направление, не мог придти к наблюдениям, которые возникли у Римана, применившего нехитрый прием – в 1/ns степень s стала комплексной. В итоге отрезок пути, не меняя протяженности, описываемой модулем комплексного числа, обзавелся сменой направления. Отсюда понятным становится, что путник, при соответствующем выборе s, вполне может повернуть назад и оказаться рядом с началом пути. Для иллюстрации приведем построенный нами один из характерных графиков перемещения путника Орема с учетом смены направления пути по Риману (рис. 1).
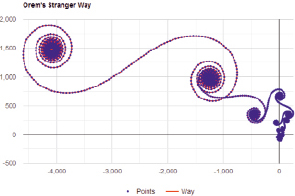
Рис. 1. Путь путника Орема по формуле Римана
Как видно, бесконечность пути нисколько не мешает нам устанавливать конечную дистанцию, которую он пройдет до точки своего финального завихрения. Характерные похожие на клотоиды эволюции этого пути возникают благодаря дискретности модели – аналогичные эволюции совершают колеса автомобилей на кинопленке, катящиеся назад. Физики любят математические модели с бесконечностями, они позволяют водить разного рода виртуальные частицы и даже порождать их из вакуума. Объясняя тем самым парадоксы, которые сложно объяснить в рамках более мирной математики. Парадокс Рамануджана, в частности, объясняется тем, что при вариации s путник прибывает в точку, близкую к –1/12 (назад) примерно так, как это показано на рис. 1. Рассматриваемый параметр s=–1 как предельная точка сэта таких настроек, она ничего парадоксального в себе не содержит и доступна пониманию продавца селедки. А ведь люди еще в начале прошлого века считали подобное равенство суммы положительных натуральных чисел отрицательной дробной величине поводом для размещения в психлечебнице. О чем и пишет не без юмора клерк из Индии профессору Харди.
Анимированные физические модели
Физические модели развивал своим дифференциальным исчислением Эйлер, установивший разложение экспоненты на гармоники. В теории динамических систем неустойчивость, описываемая экспонентой, не является поводом для отказа от понятия статического коэффициента. Блуждания могут быть в том числе и расходящиеся. Парадоксы условно суммируемых рядов нас не касаются, поскольку они строятся на обыденном для динамических систем материале – нельзя передергивать и переставлять точки движения.
В самом деле, не все равно, когда вы выстрелили в танк. До обеда или после обеда. Сообразно вашему выбору он и остановится, чего же в этом странного или удивительного.
Не стоит забывать, однако, что и Эйлер, и Риман жили задолго до установления сложившейся терминологии динамических систем. Они нарабатывали свои понятия и представления, которыми часть специалистов охотно пользуется. Риман не мог не отметить, что перестановки негативно сказываются на однозначности итогов суммирования. Эйлер же указывал выход, который он ощущал в дифференциальном исчислении. Подчеркивая физичность нашей модели, мы наработали 3D-модель путника (рис. 2).

Рис. 2. Модель путника Орема
Следуя логике Римана, он ходит следующим образом. В каждой точке останова, отвечающей значению частичной суммы ряда, он приподнимает ногу и делает пируэт – поворот на описываемый фазой 1/ns угол. Далее он, собственно, ничем не отличается от путника Орема или Эйлера, проходя дистанцию, описываемую модулем. То есть, если он без поворотов проходил расстояние, пропорциональное квадрату числа π, то он и будет его проходить. Это будет, если учитывать повороты, длина его криволинейного пути. Расстояние до конечной точки, куда он дошел, совершая блуждания, естественно, окажется иным – ведь мы измеряем его в метрике, никак не связанной с путем. Шагомером солдат не пользуется.
Вид путника Орема на рис. 2 напоминает деревянного солдата из сказки про Урфина Джюса и выбран нами в силу простоты сборки макета из «полешек-цилиндров». Эта форма удобна для передачи ее примитивами распространенной трехмерной браузерной графики Three.js. Приведенная графическая модель, среди прочих, хранится на сайте [5]. В работах студентов это могут быть иные персонажи сказок, например, Красная Шапочка, которой пируэт на одной ножке больше подходит, чем дуболому.
При качественной анимации это могут быть достоверно похожие на людей персонажи с их мыслями, эмоциями (усталость) и прочим. Нам кажется это большим и интересным направлением трехмерной анимации сходных математических задач. Интересным является также то, что можно построить такую же графическую интерпретацию, только не пути, а изменений комплексного коэффициента усиления релейной линии, описываемой добавкой Л. Эйлера 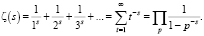 Оба эти метода должны дать одинаковый результат. Сложность пути при большом значении мнимой части аргумента можно оценить по графику (рис. 3), который мы не случайно назвали «картой Европы».
Оба эти метода должны дать одинаковый результат. Сложность пути при большом значении мнимой части аргумента можно оценить по графику (рис. 3), который мы не случайно назвали «картой Европы».
Из всего этого сложного пути, анимация построения которого представлена на сайте [5], показывающем множество еще других частных деталей, берется одна конечная точка, слагающая аттрактор второго уровня.
Область недостижимости
Аттрактор второго уровня описывает место, куда устремлен путник. В силу того, что путь «складывается» из блужданий путника и что компромиссный взгляд Л. Эйлера описывает конечную точку пути как точку уравновешивания колебаний (среднюю точку), аттрактор второго уровня не столь далеко отходит от нуля, как это происходит, например, в случае однонаправленного движения. Риман следовал Гауссу, занимавшемуся интерпретацией точек на плоскости числами. Можно добавить еще и третью ось времени n, выстраивая не некий обобщенный фазовый портрет, а аналог интегральной кривой. Причем этот аналог может касаться также аттрактора второго уровня (конечные точки путей), который строят двумерным, а мы изобразим в 3D-графике трехмерным, откладывая вверх значение мнимой части s. Как видно из рис. 4, если модуль степени усталости s больше 1/2, то между вертикальной осью от нуля и аттрактором возникает цилиндр области недостижимости. То, что его диаметр больше 0, составляет содержание знаменитой гипотезы Римана.
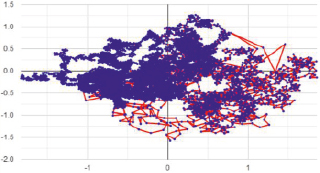
Рис. 3. Путь путника, напоминающий карту Европы
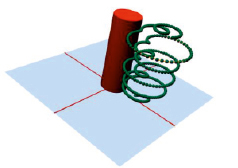
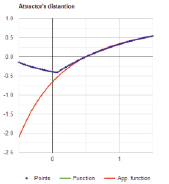
Рис. 4. Аттрактор конечных точек и график радиуса области недостижимости
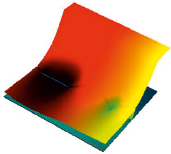
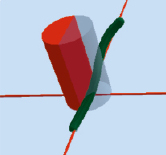
Рис. 5. Близкие нули и нарушение аттрактором границы области недостижимости
Витки дзета-функции (а также и пути путника!) не заходят в область недостижимости, образованную отчасти усталостным (периметром пути), отчасти кинематическим фактором (его извилистостью). Это касается сколь угодно сложного пути, а предела фрактальной сложности нет. Иными словами, показатель степени s (за вычетом 1/2) вполне может играть роль искомого Оремом импетуса, то есть первого представления об энергии или, вернее, дефиците энергии, не позволяющей достичь нужной точки. Древние исследователи представление об этом имели, хотя бы в единицах запасов пищи для путников.
Оценка радиуса области недостижимости и теорема Воронина
Рассмотрим масштабирующий множитель M = a(a–1)π–a/2Г(a/2)/2 кси-функции ξ = Mζ, проходящий через нуль в точке Re(s) = a = 1. Будучи наращен добавкой (1/4)!/2π 1/4, он дает оценку радиуса области недостижимости, отмеченную на рис. 4 красным цветом и откладываемую вниз левее точки пересечения нуля. Синим цветом отмечены реальные оценки дистанции до нуля, вычисленные на ограниченном диапазоне изменений мнимой части. Выброс с изломом синей кривой обеспечен первым минимумом модуля дзета-функции вблизи вещественной кривой. Таким образом, область недостижимости корректируется минимумами, особенно сильными в окрестностях сближения нулей. Первое сближение трех нулей на критической линии a = 1/2 в области значений их мнимой части b = 7563.183, 7563.520, 7563.769 дает сильный спад функции (рис. 5).
Возможное доказательство гипотезы Римана состоит в выяснении характера синей кривой (рис. 4), учтен пока только один крупный минимум. Изломы понижают значение ее, но поскольку таких точек неограниченное множество, можно предположить, что радиус области достижимости описывается аналитической функцией и, согласно теореме С.М. Воронина [6], точно так же как и его первое приближение красной линией, он описывается фрагментом смещенной дзета-функции. Поскольку она монотонна, то это обеспечивает гипотезу Римана гарантией, что нули встречаются только при a = 1/2.
Кроме путника Дзета можно ввести путника Эту, манера движения которого изменена на периодически повторяемый попятный шаг. Хорошо известно, что траектории обоих путников связаны простой аналитической зависимостью, но путник Эта движется медленнее. Поэтому он имеет не одну, а две критические полосы и две цепочки нетривиальных нулей. Иными словами, это расщепление пути путника Орема – Римана, подобное расщеплению линий спектра, очень характерное для задач детерминированного хаоса.
При пристальном изучении оказывается, что походок и путников больше и все они имеют физическую интерпретацию, что и привело Майкла Атью к физической трактовке дзета-функции, вплоть до учета мировых констант физики в доказательстве гипотезы Римана [3]. Известно, что Атья широко пользовался аппаратом сложных преобразований, до сих пор изучаемых и разбираемых математическим сообществом. Пары близких нулей напоминают пары простых чисел, образующих составное число. Так как составные числа объясняют нарастающую редкость простых чисел, еще Гаусс заподозрил (а Риман это выразил), что комплексы нулей повторяют логику появления простых чисел. Возможно, инверсно, при движении от бесконечности, так как закон Грама начала прошлого века описывает равномерное следование нулей на критической полосе, позволяющее вычислять межи между ними. Парность, нарушающая закон Грама, стягивает траектории к нулю, образуя предпосылки для поиска некоторых ведущих (к минимумам) нулей вне критической прямой.
Отечественный математик Анатолий Карацуба не только заметил, что модуль функции подтягивается к нулю при наличии пар близких нулей, но и исследовал это явление. Множество тонких и весьма точных рассуждений А. Карацубы и его ученика М. Королева обращает нас к учету этого важного случая. Можно вводить и рассматривать пары близких путников. Это изложено на учебных серверах [5, 7] и породило цепочку 3D-анимаций, с которыми можно ознакомиться там же по их демонстрационным версиям.
Заключение
В своих выпускных квалификационных работах соавторы статьи – студенты описали более детально все исторические параллели и технические особенности, послужившие основой для этой первой публикации.
Работа удачно вписалась в учебный процесс кафедры вычислительных систем и сетей ФГАОУ ВО «Санкт-Петербургский государственный университет аэрокосмического приборостроения», так как во время самоизоляции, связанной с пандемией коронавируса COVID-19, примеры на сайтах, выполненных с использованием технологии «Живая книга» [4, 5, 7], послужили основой для построения анимаций не только при исследовании дзета-функции Римана, но и задач поиска ортогональных матриц Адамара, биологического компьютинга, моделей механических стендов и многого другого.

