Паразитология – комплексная наука, включающая в себя биологическую компоненту – исследующую фундаментальные закономерности паразитизма, медицинскую – описывающую взаимоотношения паразита и человека, ветеринарную – исследующую паразитов домашних и сельскохозяйственных животных, агрономическую, или фитопатологию – изучает паразитов растений, и экологическую компоненту – описывающую взаимодействия организмов паразитов между собой и с их средой обитания, включающей климатические и географические факторы. Это отразилось на методологии паразитологии, впитавшей в себя математические и статистические подходы, характерные для вышеописанных дисциплин, и дополнившей её специфическими приемами. Однако в большинстве работ паразитология выступает в качестве прикладной дисциплины, в которой наибольшей популярностью пользуется индексный метод.
Экстенсивность инвазии ЭИ (Prevalence) – процент хозяев, зараженных одним паразитом или группой [1–3]:
ЭИ = Np/n×100 %. (1)
Однако в том случае, когда в качестве зараженных хозяев выступают люди, принято использовать эпидемиологические показатели – количество случаев на 100 тысяч населения [4].
Интенсивность инвазии ИИ (Intensity) – среднеарифметический показатель числа паразитов, приходящихся на одну зараженную особь хозяина [3; 5]:
ИИ = Par/ Np, (2)
где Par – число выявленных паразитов у Np зараженных хозяев. Полученные результаты для удобства восприятия могут быть представлены в форме полуколичественных данных, + – слабая интенсивность инвазии; ++ – средняя; +++ – сильная интенсивность инвазии [5]. Достаточно часто вместо среднего значения представляют амплитуду ИИ [6], что значительно затрудняет оценку достоверности полученных результатов и сравнение данных, полученных в разных исследованиях.
Индекс обилия ИО (Abundance) – среднее значение количества особей выбранного одного или нескольких видов паразитов у всех особей хозяина, включая незараженных [1; 2]:
ИО = Par/ n, (3)
где Par – количество выявленных паразитов у n обследованных животных.
Отдельно стоит проблема оценки достоверности различия двух индексов. В классических работах предлагаются следующие формулы. Критерий достоверности разностей двух оценок ЭИ (Федоров, 1986):
t dif = (P1 – P2)/√( M 2 p1 + M 2 p2);
MP = √ (P (100 – P )/ n), (4)
где Р1, Р2 – сравниваемые ЭИ, %; МР1, МР2 – их ошибки; n – число исследованных хозяев.
Критерий достоверности различия показателей ИО рассчитывается по формуле П.В. Терентьева и Н.С. Ростовой (1977):
t = (X1 – X2)/ F; F = √ (S12 (n – 1) + S22 (n – 1)/( n1 + n2 – 2)) *√(n1 + n2) /(n1 n2), (5)
где Х1, Х2 – сравниваемые показатели ИО; S12, S22 – их среднеквадратические отклонения; n1, n2 – размеры сравниваемых выборок (число исследованных хозяев). Полученные величины сравниваются с табличными, из таблицы распределения Стьюдента t (α, df) (обычно при уровне значимости α = 0,05) при числе степеней свободы (df = n – 2).
Однако представленные критерии неудобны для использования, поэтому в большинстве работ они отсутствуют [1; 5; 6]. По-видимому, это объясняется их громоздкостью и широким внедрением автоматизированных методов определения достоверности отличия двух выборок, реализованных в электронных таблицах Excel [1; 7], пакете программ Statistica [1; 8] и др. Их место, как правило, заменяет t-критерий Стьюдента. Впрочем, его использование, также не всегда оправданно, поскольку требует проверки соответствия распределения изучаемой выборки нормальному. Однако существуют данные о том, что в большинстве случаев распределение гельминтов в популяции описывается биномиальным распределением или его предельным случаем распределением Пуассона–Борткевича. Это определяет необходимость использования непараметрических методов оценки достоверности различия двух выборок, таких как F-критерий Фишера [8] или критерий согласия Пирсона χ2 [9].
Влияние биологической и экологической компоненты обусловило включение в методологию паразитологии следующих индексов: индекс Шеннона (H), индекс Бриллуэна (HB), индексы Жаккара для качественных (СJa) и количественных данных (IJ) (индекс Серенсена) [1; 2; 10].
Индекс Шеннона представляет собой меру хаоса, энтропии. Последняя будет максимальной, когда все события (S) будут иметь одинаковую вероятность наступления (рi = 1/S) (Лебедева и др., 1999):
H’ = -Σpi ln pi, (6)
где рi – доля гельминтов i-го вида.
Причины ошибок в использовании этого индекса чаще всего заключаются в том, что авторы включают наблюдаемые или исследуемые виды, а не все их существующее в природе разнообразие. Таким образом, количество i в разных исследованиях может быть совершенно разным, а полученные результаты – несопоставимыми для разных исследований, или даже некорректными в случае искусственного исключения из рассмотрения какого-либо вида паразита. Особенностью этого индекса является то, что его распределение соответствует нормальному, что позволяет использовать методы параметрической статистики, дисперсионный анализ и t-критерий Стьюдента [11].
Индекс Бриллуэна (HB) также используется для оценки качества экосистемы, однако при оценке одного и того же массива первичных данных он принимает более низкие значения, чем H. Это связано с тем, что в нем нет неопределенности, свойственной индексу Шеннона. В связи с этим HB рекомендуется использовать при оценке коллекции.
HB = (ln N ! – Σ ln ni !)/N, (7)
где N – количество в сообществе особей всех видов; ni – количество особей вида i; ! – знак факториала.
В паразитологии Н и HB дополняют друг друга. Посредством H характеризуют разнообразие компонентного паразитарного сообщества (паразитарное сообщество популяции хозяина), а НВ – разнообразие инфрасообщества (паразитарное сообщество у отдельной особи хозяина). Иногда встречается полуколичественный способ оценивания видового разнообразия, в баллах [12].
Близость видового состава паразитов и их обилия можно оценить с помощью индексов Жаккара для качественных (СJa) и количественных данных (IJ):
C Ja = j/(a + b + j), (8)
где j – число общих видов на обоих участках; a – число видов на участке А; b – число видов на участке В (Мэгарран, 1992).
IJ (j, k) = Σ min(nij, nik) / Σ max (nij, nik), (9)
где nij – количество i-го вида в сообществе j; nik – количество i-го вида в сообществе k. Полученные значения индексов Жаккара могут быть положены в основу кластерного анализа, для построения дендрограмм сходства, которые позволяют выявлять группы, близость параметров которых обусловлена общностью физиологических процессов [13].
Доминирование отдельных видов в сообществе гельминтов определяется с помощью индекса доминирования Ковнацки (D) [14]:
Di = 100×pi×Ni/Ns, (10)
где pi – встречаемость; pi = mi/Mi, mi – число проб, в которых был найден вид i гельминтов, M – общее число проб, Ni – число особей i-го вида гельминтов, Ns – общее число особей в биоценозе. Группы доминирования гельминтов: 100-10 – доминанты; 10-1 – субдоминанты; 1-0,001 – адоминанты.
Также встречаются такие индексы, как среднее число паразитов на 1 кг массы, количество живых и мертвых личинок, которое может быть выраженно некачественно, в баллах [6].
Индекс сезонности позволяет дать количественную оценку сезонных колебаний и показывает, на сколько процентов изучаемое явление больше или меньше среднегодового уровня. Сезонный характер животноводческого производства, связь цикла развития паразитов с климатическими факторами настойчиво диктует необходимость работы с динамическими рядами данных. Существует достаточно большое количество способов рассчитать индексы сезонности, построенных на усреднении отклонений исходных уровней ряда динамики от каких-либо эталонных значений: средней, медианы, теоретических значений тренда и т.д. Из всего многообразия можно выделить два способа расчета индекса сезонности Is [15]. Первый ориентирован на ряды динамики, не имеющие тренда. Он построен на определении отклонений усредненных значений для каждой временной точки (квартала, месяца, недели) от средней величины.
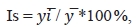(11)
где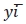 
– среднее значение одноименных месяцев (кварталов); 
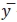– среднее значение уровней ряда дина
мики.Второй метод расчета индекса сезонности подходит для динамических рядов, содержащих в себе тенденцию, на фоне которой происходят отклонения. Он основан на расчете среднего значения из соотношений эмпирических и теоретических уровней ряда динамики:
Is = ∑(Yi / Yti)/n *100 %, (12)
где Yi – эмпирические значения для каждой временной точки ряда; Yti – теоретические значения, полученные по уравнению тренда; n – количество временных точек.
Учитывая частое использование динамических рядов, большую пользу может принести определение коэффициента корреляции, который в работах чаще всего представлен коэффициентом корреляции Пирсона (r) [7; 16]. Ранговые коэффициенты корреляции применяются значительно реже [10], однако использование их предпочтительнее, поскольку они позволяют описывать взаимодействие не только количественных первичных данных, но и полуколичественных, баллов и индексов, часто применяемых в паразитологии. Очевидная трудность в интерпретации большого численного массива коэффициентов корреляции может быть успешно решена при помощи использования метода корреляционных плеяд [17].
Выявление тренда [10; 18] в рядах индексов или первичных данных является эффективным способом выявления общей тенденции, что особенно полезно при широком видовом составе гельминтов и их промежуточных хозяев. Однако это методика, являющаяся частным случаем регрессионного анализа, исследующего влияния одной или нескольких независимых переменных на зависимую переменную. Использование его методов позволяет не только сглаживать флуктуации исследуемых параметров, но и выявлять взаимосвязи между ними, характер этих связей, что в свою очередь позволяет математически прогнозировать состояние паразитарных систем в зависимости от внешних факторов, например температуры [19] или осадков [20]. Полный список экзогенных факторов, влияющих на прогноз состояния паразитарных систем, более широкий и включает в себя [21]:
1. Сведения о климате и орографии местности хозяйства, численности и технологии содержания животных, их возрастных группах, пастбищеобороте.
2. Характеристика пастбищ.
3. Диагноз гельминтоза, вид возбудителя, моно- или полиинвазия.
4. Эпизоотология – возникновение, течение, сезонная и возрастная динамики.
5. Биология промежуточных и дополнительных хозяев (моллюсков, почвенных клещей, муравьев и т.п.).
6. Метеорологические показатели в течение выпасного периода – осадки, температура, инсоляция.
Возможность прогнозирования состояния паразитарных систем оказалась настолько заманчивой, что обусловила ряд публикаций по прогнозу того или иного гельминтоза. К сожалению, большинство из этих прогнозов носят качественный характер, без привлечения математического или статистического аппарата, что, безусловно, снижает их ценность [22–24]. Гораздо привлекательнее выглядит полуколичественный алгоритм, базирующийся на точных математических данных [25].
Специальных знаний требует использование разработанных для экологических исследований математических моделей систем уравнений, разработанных для экологических исследований, таких как модель МакКормика/Кендрика [26], модель Никольсона-Бейли [27] и другие [28].
К сожалению, в ряде паразитологических исследований результаты представлены только абсолютным количеством наблюдаемых случаев и их долей в 100 % наблюдений [29–31]. Часто вместо средней и её ошибки используется диапазон – минимальные и максимальные значения параметра [3; 32], что снижает сопоставимость результатов, полученных разными авторами, так как требует учета распределения и объема исследуемой выборки.
Безусловно, полноценное использование метода индексов, статистического и математического аппарата позволит не только обогатить полученные результаты исследования, сделать их более релевантными, но и обеспечить сопоставимость результатов разных авторов.