Наиболее важными источниками социальной напряженности в любой стране многие исследователи считают экономические проблемы: повышение цен, безработица, низкая оплата труда, разница в доходах населения страны. Данные проблемы исторически являются одними из важнейших вопросов экономики. Успешность государственной политики зависит в той или иной мере от распределения доходов между группами населения в стране. Другими словами, преодоление социального неравенства должно являться одной из главных задач системы государственного управления России как социального государства [1].
Для того чтобы определить пути выравнивания уровней доходов государственной распределительной политики, могут быть использованы специальные методы измерения и количественной оценки дифференциации доходов.
Цель исследования: оценить распределение доходов между различными группами населения в России за 2019 г. с помощью метода оценки дифференциации дохода между разными группами населения кривой Лоренца и измерить степень неравенства дохода количественно с помощью коэффициента Джини.
Материалы и методы исследования
Для анализа дифференциации доходов населения рассмотрим метод оценки распределения доходов – кривую Лоренца, которую разработал в 1905 году американский ученый М. Лоренц. Кривая Лоренца – это статистическая зависимость между долей дохода, которая приходится на различные процентные группы населения.
При построении кривой Лоренца, в прямоугольной системе координат по оси абсцисс откладываются процентные группы населения, по оси ординат – доли дохода, получаемые этими группами (рис. 1).
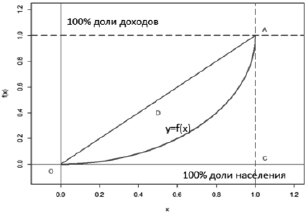
Рис. 1. Кривая Лоренца
«М. Лоренц установил, что при равном распределении доходов 20 % населения получают 20 % всего дохода, 40 % населения – 40 % всего дохода» и т.д. [2] Таким образом, можно построить прямую ОА (рис. 1), уравнение которой у = х и которая отражает теоретическое абсолютное равенство распределения всего дохода.
Тогда ломаная ОСА (рис. 1) отражает абсолютное неравенство, т.е. 20, 40, 60 и 80 % населения не получают никаких доходов, 100 % всего дохода присваивает одна группа населения – точка С.
В действительности же распределение доходов населения неравномерно, что и отражает функция у = f(x) (рис. 1), т.е. кривая Лоренца. Вогнутость кривой Лоренца позволяет судить о степени неравенства доходов в экономике [3].
Для функции y = f(х) выделим следующие свойства:
1. Область определения функции x∈[0; 1], область значения функции f(x)∈[0; 1], где за 1 принимается 100 % дохода, 100 % населения.
2. Функция f(x) возрастает на всей своей области определения, т.к. группа населения, относящаяся к более высокой процентной группе, будет получать большую часть всего дохода.
3. Функция y = f(х) выпукла вниз на всей своей области определения и находится ниже отрезка ОА. Иначе, чем ближе отклоняется кривая Лоренца в сторону оси Х, тем в распределении доходов наблюдается большее неравенство.
Кривая Лоренца – это графическое изображение зависимости между долей дохода, которая приходится на различные процентные группы населения, а для того чтобы измерить степень неравенства дохода количественно, используют различные коэффициенты: коэффициент Джини и коэффициент Гувера.
В этой статье остановимся на нахождении коэффициента Джини, который является статистическим показателем, оценивающим экономическое равенство. Коэффициент Джини равен отношению площади фигуры, ограниченной прямой абсолютного равенства и кривой Лоренца, к площади фигуры, ограниченной прямой абсолютного равенства и ломаной абсолютного неравенства [2].
Обозначим фигуру, ограниченную прямой у = х и кривой Лоренца у = f(x), через D (рис. 1). Тогда коэффициент Джини будет находиться по следующей формуле:
.
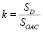Найдем площадь треугольника ОАС, как площадь прямоугольного треугольника с катетами, равными 1. Следовательно, площадь треугольника ОАС равна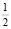 
. Тогда коэффициент Джини будет находиться по следующей формуле:
k = 2•SD.
Исходя из полученной формулы, можно определить следующие свойства коэффициента Джини:
1) величина площади фигуры SD находится в пределах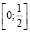 
, тогда коэффициент Джини находится в интервале от 0 до 1;
2) если площадь фигуры SD стремится к нулю, тогда кривая Лоренца приближается к прямой ОА, т.е. доходы распределены более равномерно. Другими словами, когда доходы распределены более равномерно, коэффициент Джини стремится к нулю;
3) если площадь фигуры SD стремится к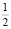 
, тогда кривая Лоренца приближается к оси Х, т.е. доходы распределены менее равномерно. Другими словами, когда доходы распределены неравномерно, коэффициент Джини стремится к единице;
4) исходя из п. 3 следует [4]:
– при коэффициенте, равном 0 – полное равенство в доходах населения;
– при значении коэффициента менее 0,3 – слабое неравенство в доходах населения;
– при 0,3–0,7 – значительное неравенство в доходах населения;
– при значении более 0,7 – сильное неравенство в доходах населения;
– при коэффициенте, равном 1 – абсолютное неравенство в доходах населения;
5) если кривая Лоренца задана непрерывной функцией y = f(х), то площадь области D находится как площадь криволинейной трапеции.
Согласно предварительным данным за 2019 г. дифференциация денежных доходов в России не изменилась, и распределение по 20-процентным группам осталось таким же, как и в 2018 г. (табл. 1) [5].
Результаты исследования и их обсуждение
Преобразуем данные из табл. 1 в доли (табл. 2).
Исходя из данных табл. 2 кривая Лоренца имеет вид (рис. 2).
Оценим степень неравенства дохода с помощью коэффициента Джини. Для этого необходимо найти площадь области D, т.е. найти площадь криволинейной трапеции. Следовательно, кривую Лоренца необходимо представить в виде непрерывной функции.
Проведем аналитическое выравнивание кривой Лоренца методом регрессионного анализа. Так как кривая Лоренца – это статистическая зависимость двух признаков, для подбора вида уравнения регрессии используем графический метод. Он основан на поле корреляции. Используя данные, представленные в табл. 2, аппроксимируем их различными функциональными зависимостями и подберем ту, которая имеет наибольший коэффициент детерминации. В электронных таблицах воспользуемся командой «Добавить линию тренда» на гистограмме, отобразив уравнение тренда и коэффициент достоверности аппроксимации – коэффициент детерминации (рис. 3).
Таблица 1
Распределение общего объема денежных доходов по 20-процентным группам населения за 2019 г. в России [5]
|
20-процентные группы населения, % |
Доход, % |
|
0 |
0 |
|
20 |
5,3 |
|
40 |
15,3 |
|
60 |
30,3 |
|
80 |
52,9 |
|
100 |
100 |
Таблица 2
Распределение общего объема денежных доходов по 20-процентным группам населения за 2019 г. в России [5]
|
Доли населения |
Доля дохода |
|
0 |
0 |
|
0,2 |
0,053 |
|
0,4 |
0,153 |
|
0,6 |
0,303 |
|
0,8 |
0,529 |
|
1 |
1 |
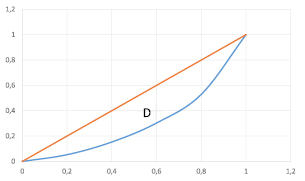
Рис. 2. Кривая Лоренца за 2019 г.
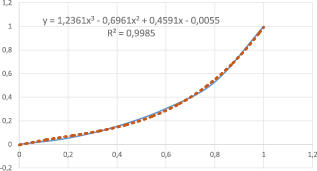
Рис. 3. Аналитическое выравнивание кривой Лоренца
Коэффициент детерминации R2 = 0,9985 показывает, что 99,85 % вариации доли доходов объясняется вариацией процентной группы населения, а 0,15 % приходится на долю прочих факторов.
С помощью F-критерия Фишера оценим качество построенного уравнения регрессии в целом. Для этого найдем фактическое значение F-критерия:
Fфакт =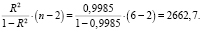 
Табличное значение F-критерия по таблице Фишера для числа степеней свободы k1 = 1, k2 = n – 2 = 4 и для уровня значимости α = 0,05 равно Fтабл = 7,71.
Исходя из того что Fфакт > Fтабл, то построенное уравнение в целом является значимым.
Следовательно, уравнение кривой Лоренца
y = f(x) = 1,2361x3 – 0,6961x2 + 0,4591x – 0,0055.
Далее найдем площадь области D как площадь криволинейной трапеции. Так как область D ограничена двумя кривыми, то для нахождения площади фигуры будем использовать формулу
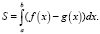
Исходя из того что область D ограничена прямой у = х и кривой Лоренца y = f(x) на отрезке x∈[0; 1], тогда формула нахождения площади области D примет следующий вид:
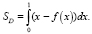
Подставим вместо f(x) полученную ранее функцию для кривой Лоренца и вычислим определенный интеграл на отрезке [0; 1]:
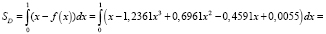
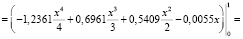
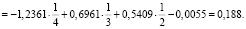
Следовательно, коэффициент Джина равен
k = 2•SD = 2•0,188 = 0,376.
Выводы
Учитывая свойства коэффициента Джини и исходя из того что он равен примерно 0,376, считаем, что это говорит о достаточно неравномерном распределении доходов среди населения в России в 2019 г. Другими словами, полученное значение коэффициента Джини говорит о том, что в стране необходимо активизировать государственную политику в части преодоления разницы в доходах населения страны.
Дифференциация доходов среди населения может быть измерена различными методами, отражающими не только степень неравенства доходов среди различных групп населения, но и более сложные подходы в определении потребительских возможностей получаемых доходов. Также и для измерения величины денежного дохода существуют различные подходы. Поэтому для выявления самой проблемы экономического неравенства доходов населения достаточно найти, например, коэффициент Джини, а для более комплексного изучения вопроса социальной напряженности в стране, конечно, нужно рассмотреть и другие методики оценки распределения доходов среди населения.