Scientific journal

International Journal of Applied and fundamental research

ISSN 1996-3955

ИФ РИНЦ = 0,593

Прогресс в области наземного и воздушного транспорта сопровождается ростом уровня требований к аэродинамическим характеристикам транспортных средств. Одной из основных задач аэродинамики является расчет сил взаимодействия газового потока с поверхностью обтекаемого твердого тела. Современный уровень развития вычислительной техники позволяет моделировать этот процесс для различных, зачастую очень сложных, аэродинамических систем [1; 2]. Однако нельзя утверждать, что теоретические аспекты действия потока газа на тело полностью исследованы.

В неподвижном относительно некоторой поверхности объеме газа каждая его молекула участвует в тепловом хаотическом движении. Основное уравнение МКТ позволяет рассчитать статическое давление газа, близкого по своим свойствам к идеальному: 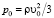, где ρ – плотность газа, υ₀ – средняя квадратичная скорость молекул. В движущемся объеме газа молекулы перемещаются хаотически и в то же время участвуют в направленном движении потока. В работах [3; 4] скорость каждой молекулы в некоторый момент времени рассматривается как геометрическая сумма вектора тепловой скорости 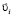и вектора скорости газового потока 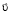: 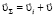(рис. 1). Давление потока p на элемент поверхности ΔS сопоставляется со статическим давлением p0. Плотность газа в неподвижном относительно поверхности объеме равна плотности газа в потоке, также одинаковы температуры. Газовый поток является плоским, безвихревым, стационарным.

На основании относительной скорости потока 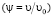и направления скорости потока (угол α, рис. 1) рассчитывается относительное динамическое давление η [3; 4]:

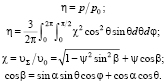(1)

Углы θ и φ характеризуют направление суммарной скорости молекулы в системе координат, связанной с элементом поверхности. Угол β – угол между суммарной скоростью молекулы и скоростью потока.

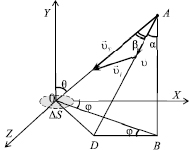
Рис. 1. Характеристики движения молекулы в газовом потоке

Если направленного движения газа нет, то отношение скорости потока к среднеквадратичной скорости молекул ψ = 0. Относительное динамическое давление в этом случае равно единице. Если скорость потока направлена к поверхности и α = 0 (рис. 1), то относительное динамическое давление потока η имеет максимальное (для данного ψ) значение. В случае движения газового потока от поверхности (α = 180 °) значение η минимально. Если поток газа движется параллельно поверхности (α = 90 °), то увеличение его скорости приводит к уменьшению давления. Полученные результаты [3; 4] согласуются в качественном отношении с широко известными экспериментальными данными.

Расчет давления газа на поверхность движущегося цилиндра

Внимание многих исследователей привлекает процесс поперечного обтекания бесконечного кругового цилиндра. Структура поля течения возле цилиндра и его аэродинамические характеристики при различных свойствах набегающего потока подробно изучены экспериментально и теоретически [5–7]. В данной работе на основании выражения для относительного давления потока (1) рассчитано распределение давления по поверхности цилиндра при его движении в среде идеального газа. Круговой цилиндр находится в неподвижной системе отсчета XYZ, ось цилиндра расположена параллельно оси ОZ (рис. 2). Ось ОZ перпендикулярна плоскости чертежа. Длина образующей цилиндра намного больше его диаметра. Цилиндр движется с небольшой скоростью υ_c в отрицательном направлении оси ОX. Линиями, параллельными оси цилиндра, его криволинейная поверхность разделена на N одинаковых по величине элементов. Если N – достаточно большое число, то каждый из элементов можно считать плоским. Положение элемента поверхности цилиндра задается углом γ, отсчитываемым по часовой стрелке от области отрицательных значений на оси ОX.

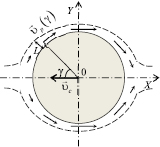
Рис. 2. Схема скоростей направленного движения молекул газа в прилегающем слое

При движении цилиндра слои газа, прилегающие к его поверхности, деформируются, так как цилиндр непроницаем для молекул. Толщина слоя, прилегающего к поверхности цилиндра, меняется от некоторого начального значения до минимальной величины вблизи миделева сечения. На большом удалении от цилиндра газ в системе отсчета XYZ неподвижен, его молекулы участвуют только в тепловом хаотическом движении. Вблизи поверхности цилиндра, вследствие уменьшения толщины прилегающего слоя, молекулы приобретают в системе отсчета XYZ некоторую скорость направленного движения 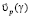. Эта скорость направлена по касательной к поверхности цилиндра и меняется от нуля (для γ = 0) до некоторого максимального значения в миделевом сечении. В простейшем приближении можно принять, что модуль скорости этого направленного движения газа в прилегающем слое зависит от угла γ следующим образом:

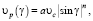(2)

где a – коэффициент, характеризующий степень сжатия слоя. Чем сильнее прилегающий слой сжат, тем больше коэффициент a. В классическом случае бесциркуляционного обтекания кругового цилиндра идеальной средой a = 2, а n = 1 [8].

В системе отсчета, связанной с цилиндром, каждый элемент объема поверхностного слоя газа участвует в двух направленных движениях: со скоростью 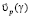и со скоростью 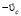, равной скорости поступательного движения цилиндра, но противоположно направленной.

Для значений угла γ от 0 до 360 ° (рис. 2) с шагом в один градус были рассчитаны:

– скорость направленного движения потока газа в слое, прилегающем к элементу поверхности цилиндра (2), возникающая вследствие сжатия прилегающего слоя;

– тангенциальная составляющая скорости направленного движения элемента объема потока относительно прилегающего элемента поверхности цилиндра (с учетом сжатия прилегающего слоя и поступательного движения цилиндра):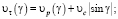

– нормальная составляющая скорости направленного движения элемента объема потока относительно прилегающего элемента поверхности цилиндра: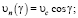

– скорость направленного движения элемента объема газа относительно прилегающего элемента поверхности: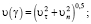

– отношение скорости направленного движения в потоке возле элемента поверхности к среднеквадратичной скорости теплового движения молекул: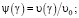

– величина угла α(γ) между вектором скорости направленного движения 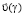возле элемента поверхности и нормалью к этому элементу (рис. 1);

– относительное динамическое давление η(γ) (1), равное отношению давления потока (динамического давления) к статическому давлению.

Полученное в результате расчетов распределение относительного динамического давления по поверхности цилиндра для различных его скоростей (в случае a = 2, n = 1) представлено на рис. 3.

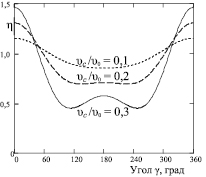
Рис. 3. Распределение относительного давления потока (1) по поверхности кругового цилиндра при различных скоростях движения цилиндра

Увеличение скорости цилиндра приводит к возрастанию разности давлений газа на его лобовую и кормовую части (рис. 3). Кроме того, при увеличении скорости возникают области минимума давления. При единичном показателе степени n (2) минимум давления на поверхность цилиндра соответствует углам γ, равным 110–120 ° и 240–250 ° (рис. 3). Такое распределение давления по поверхности цилиндра коррелирует в качественном отношении с результатами экспериментов [8; 9]. Области минимального давления на поверхность цилиндра, найденные экспериментально, располагаются вблизи миделева сечения (угол γ находится в пределах 70–90 ° и 270–290 °). При увеличении n в формуле (2) точки минимума давления перемещаются ближе к миделевому сечению. Так, при n = 4 минимум давления на поверхность цилиндра соответствует углам γ, равным 95–105 ° и 255–265 °.

Коэффициент лобового сопротивления кругового цилиндра, движущегося горизонтально со скоростью, перпендикулярной образующей (при условии разбиения его поверхности на N одинаковых частей):

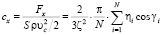, (3)

где Fx – горизонтальная составляющая силы давления, действующей на поверхность цилиндра; S – площадь миделева сечения цилиндра, ρ– плотность газа, ς – отношение скорости цилиндра к среднеквадратичной скорости молекул газа, ηi – относительное давление потока (1) для элемента поверхности, соответствующего углу γi (рис. 2).

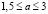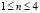В таблице 1 приведены рассчитанные значения коэффициентов лобового сопротивления цилиндра для случая: N = 360, a = 2 и n = 2 (2). При других значениях a и n (в пределах: и ) коэффициенты лобового сопротивления незначительно (от -0,2 до +0,2) отличаются от приведенных в таблице соответствующих значений.

Таблица 1

Рассчитанные (3) коэффициенты лобового сопротивления кругового цилиндра

Коэффициенты лобового сопротивления цилиндра (табл. 1) соответствуют коэффициентам, определенным экспериментально, но при очень малых числах Рейнольдса. По данным [6; 10], если число Рейнольдса увеличивается от 0,1 до 10, то экспериментально определенный коэффициент лобового сопротивления цилиндра меняется от 60 до 3.

Расчет сил действия идеального газа на поверхность движущегося полуцилиндра

На основании относительного динамического давления (1) по вышеописанной методике рассчитаны сила лобового сопротивления и подъемная сила, действующие на половину цилиндра (рис. 2), расположенную выше плоскости XOZ. Полуцилиндр движется горизонтально со скоростью υ_c. В этом случае обтекания тела идеальным газом слой потока, прилегающий к его нижней плоской поверхности, не имеет ограничений для своего движения и не деформируется. Скорость движения этого слоя (в системе отсчета, связанной с полуцилиндром) равна скорости полуцилиндра, но противоположно направлена.

Сила лобового сопротивления для полуцилиндра при указанной схеме обтекания равна половине силы лобового сопротивления для цилиндра при одинаковых условиях расчета. Коэффициент лобового сопротивления равен соответствующему коэффициенту для цилиндра (табл. 1), так как для полуцилиндра площадь миделева сечения в два раза меньше.

Коэффициент подъемной силы для рассматриваемого полуцилиндра (при условии разбиения его круговой поверхности на N одинаковых частей):

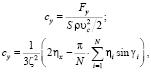(4)

где Fy – вертикальная составляющая силы давления газа, действующей на полуцилиндр; S – площадь нижней горизонтальной поверхности полуцилиндра, η_x – относительное динамическое давление для этой поверхности.

При увеличении коэффициента a в соотношении (2) возрастает степень сжатия слоя газа, прилегающего к цилиндрической поверхности. В этом случае рассчитанный коэффициент подъемной силы (табл. 2) также возрастает. При увеличении скорости полуцилиндра коэффициент подъемной силы в рассматриваемой модели меняется незначительно.

Таблица 2

Рассчитанные (4) коэффициенты подъемной силы полуцилиндра (N = 180)

Расчет сил действия потока идеального газа на поверхность вращающегося цилиндра

В данной работе рассмотрен цилиндр, вращающийся относительно своей оси в плоскопараллельном потоке идеального газа. Скорость потока υ (на бесконечном удалении от цилиндра) сонаправлена с осью ОX (рис. 2). Цилиндр вращается против часовой стрелки. Так как идеальный газ не обладает вязкостью, считаем, что поверхность цилиндра в процессе его вращения не увлекает за собой молекулы газа из прилегающего слоя. Степень сжатия прилегающего слоя для соответствующих элементов поверхности поступательно движущегося цилиндра и цилиндра, вращающегося в потоке газа, одинакова (при равных скоростях υ_с и υ). Следовательно, одинаково и распределение скоростей υ_p(γ) (2) по поверхности рассматриваемых цилиндров.

В слое газа, расположенном выше цилиндра (рис. 2), при вращении цилиндра против часовой стрелки тангенциальная составляющая скорости направленного движения элемента объема газа относительно прилегающего элемента поверхности:

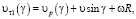
где ω – угловая скорость вращения цилиндра, R – его радиус.

В слое газа, расположенном ниже цилиндра, тангенциальная составляющая скорости элемента объема газа:

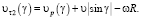
Вследствие различия этих скоростей давление потока газа на верхнюю сторону поверхности цилиндра меньше давления на нижнюю часть, вертикальная составляющая силы действия со стороны потока на цилиндр (сила Магнуса) направлена вверх. При изменении направления вращения на противоположное меняется и направление этой силы.

Коэффициент подъемной силы для цилиндра, вращающегося вокруг своей оси в потоке газа, рассчитан аналогично (4):

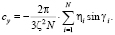(5)

Полученная зависимость коэффициента подъемной силы от отношения 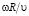(при заданных коэффициентах a и n) близка к линейной (табл. 3).

Таблица 3

Рассчитанные (5) коэффициенты подъемной силы для цилиндра, вращающегося в потоке идеального газа (N = 360)

В рассматриваемой модели коэффициент подъемной силы вращающегося цилиндра не зависит от скорости газового потока υ. При всех рассмотренных отношениях этой скорости к тепловой скорости молекул (в пределах от 0,05 до 0,15) получены результаты, представленные в табл. 3.

Коэффициенты лобового сопротивления, рассчитанные для вращающегося цилиндра, при небольших угловых скоростях (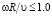), равны коэффициентам лобового сопротивления поступательно движущегося цилиндра (табл. 1) при соответствующих условиях расчета. Увеличение скорости вращения цилиндра приводит к уменьшению рассчитанного коэффициента лобового сопротивления на 0,2–0,5.

Механизм возникновения силы лобового сопротивления и подъемной силы в потоке идеального газа

Давление газа на поверхность твердого тела является результатом большого числа столкновений молекул газа с поверхностью тела. Давление газа тем больше, чем больше изменение импульсов его молекул в процессе столкновений и чем выше частота столкновений. Частицы, приближающиеся к поверхности с большой скоростью, оказывают большее силовое воздействие на тело по сравнению с молекулами, скорости которых малы (при одинаковых массах молекул и углах между вектором скорости и нормалью к элементу поверхности). Кроме того, за одно и то же время к поверхности тела приблизится большее число «быстрых» молекул, нежели «медленных».

Скорость каждой молекулы в газовом потоке можно рассматривать как геометрическую сумму ее скорости в тепловом хаотическом движении (в некоторый момент времени) и вектора скорости направленного движения потока (рис. 1). Если молекула движется к элементу лобовой поверхности тела, эта суммарная скорость превышает усредненную тепловую скорость частиц. Вектор скорости потока направлен от кормовой поверхности, поэтому движение молекул к кормовой части тела происходит за счет тепловых составляющих их скоростей. К элементу кормовой поверхности молекула приближается со скоростью, меньшей скорости теплового движения (на величину, соответствующую скорости потока). За некоторое время к лобовой части тела приближается большое число молекул, имеющих большие скорости. За это же время к кормовой части приближается меньшее число частиц с малыми скоростями. «Быстрые» молекулы оказывают большее силовое воздействие на лобовую поверхности тела в процессе столкновений, нежели «медленные» частицы на кормовую поверхность. Это различие в числе и силе столкновений молекул газа с элементами лобовой и кормовой поверхностей тела является причиной существования силы лобового сопротивления.

Рассмотрим неподвижный объем газа, прилегающий к некоторой плоскости. К малому элементу этой плоскости за время Δt приближаются молекулы, находящиеся в пределах полусферы радиуса r = υ₀Δt, где υ₀ – среднеквадратичная скорость теплового движения. Если поток газа перемещается параллельно плоскости со скоростью υ,о к элементу поверхности за время Δt приближаются молекулы, также находящиеся в пределах полусферы, но смещенной на расстояние L = υΔt по оси OX в сторону, противоположную направлению движения потока (рис. 4).

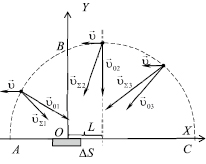
Рис. 4. Скорости молекул газа в потоке, движущемся параллельно элементу поверхности

Молекулы из меньшей части ABO полусферы перемещаются к элементу поверхности ΔS со скоростями, меньшими тепловой скорости υ₀. Действие этих молекул на элемент поверхности значительно меньше действия молекул, движущихся в направлении элемента ΔS из соответствующего неподвижного прилегающего газового объема. Молекулы из большей части BCO полусферы двигаются к элементу плоскости со скоростями, большими, чем υ₀, и их давление на элемент превышает давление соответствующих молекул из неподвижного прилегающего объема газа. Но суммарное давление молекул из движущихся объемов ABO и BCO меньше давления молекул из неподвижной прилегающей полусферы (табл. 4). Это уменьшение давления движущегося параллельно плоскости потока по сравнению с давлением молекул из неподвижного относительно плоскости объема газа тем выше, чем больше скорость направленного движения потока.

Если тело несимметрично относительно горизонтальной плоскости и находится в горизонтальном потоке газа, то слои газа, прилегающие к более выпуклой части, сжаты сильнее. Соответственно, скорости направленного движения молекул газа в слое, прилегающем к более выпуклой стороне, превышают скорости направленного движения в слое, прилегающем к менее выпуклой стороне тела. Большим скоростям соответствуют меньшие давления (табл. 4). Возникающая разность давлений создает подъемную силу в случае выпуклой верхней части тела и прижимную силу в случае выпуклой нижней части тела.

Если в горизонтальном потоке вращается осесимметричное тело, то степень сжатия слоев, прилегающих к верхней стороне и к нижней стороне тела, одинакова, но возникает разность скоростей направленного движения молекул относительно поверхности вращающегося тела, что также приводит к возникновению силы, перпендикулярной скорости потока (силы Магнуса).

Таблица 4

Рассчитанное (1) относительное динамическое давление η потока идеального газа, движущегося параллельно элементу поверхности (α = π/2)

Выводы

Метод расчета сил действия газового потока на твердое тело [3; 4], в основе которого лежит теорема о сложении скоростей (скорости теплового хаотического движения отдельной молекулы и скорости направленного движения потока), может быть применен для расчета как силы сопротивления, так и подъемной силы, в том числе силы Магнуса. При соответствующем математическом оформлении метод применим не только для плоских течений, но и для трехмерных потоков. Принцип относительности движения позволяет применить этот метод для расчета силы лобового сопротивления и подъемной силы для тела любой формы, движущегося в газовой среде с небольшой скоростью. Возможно исследование давления газа в каналах различной конфигурации.

Метод дает завышенные значения коэффициентов лобового сопротивления, так как столкновения молекул с поверхностью тела считаются абсолютно упругими, отражаются молекулы зеркально, не учтено влияние отраженных молекул на молекулы, приближающиеся к поверхности.

Этот относительно простой метод может быть использован для быстрого выбора из большого числа вариантов формы обтекаемого тела, близкой к оптимальной. На его основе возможно формирование в рамках классической физики единой теории возникновения аэродинамических сил в идеальной текучей среде.