Во всех современных системах распознавания образов увеличение скорости и улучшение точности распознавания являются двумя главными критериями. Тем не менее эти параметры обычно работают друг против друга: когда увеличивается скорость, точность уменьшается, и наоборот. Это особенно важно при работе со сложными системами, описываемыми большим числом параметров, поскольку по мере увеличения размерности данных информация, необходимая для эффективного анализа, растет в геометрической прогрессии. В 1961 г. Ричард Беллман назвал эту проблему «проклятием размерности» [1]. Увеличение размерности пространства влечет за собой множество недостатков, таких как переобучение, меньшая интерпретируемость (как следствие, меньшая точность модели) и увеличение времени обучения. Популярные подходы ориентированы на то, чтобы спроецировать информационное пространство с более высокой размерностью в пространство меньшей размерности, сохраняя как можно больше данных [2]. Методы сокращения размерности обычно следуют этому общему принципу, чтобы устранить «проклятие размерности» и другие нежелательные факторы, присутствующие в данных с более высокой размерностью. Это сокращает время обучения и тестирования, удаляя менее важные признаки, а также увеличивает точность системы. Таким образом, исследование методов сокращения размерности данных является актуальной задачей.
Цель исследования: применение методов сокращения размерности к задаче распознавания образов.
Материалы и методы исследования
В качестве задачи распознавания образов в данной работе была выбрана задача распознавания рукописных символов текста на изображениях. В качестве набора данных использован набор MNIST, который состоит из 70 000 изображений: 60 000 обучающих для обучения модели и 10 000 тестовых для оценки точности. Каждое изображение MNIST – это оцифрованная картинка одной цифры, написанной от руки, имеющая размер 28×28. Каждое значение пикселя лежит в диапазоне от 0 (представляет белый цвет) до 255 (представляет черный цвет). Промежуточные значения отражают оттенки серого. Задача состоит в распознавании цифр (от 0 до 9), поэтому имеется всего 10 классов для классификации.
Мотивация эксперимента заключалась в том, чтобы продемонстрировать, как сокращение размерности данных может привести к сокращению общего времени обработки данных и увеличению точности системы, реализованной для решения одной из задач распознавания образов.
Для выполнения цели исследования были использованы такие методы сокращения размерности, как метод главных компонент и стохастическое вложение соседей с t-распределением (t-distributed Stochastic Neighbor Embedding, t-SNE).
Метод главных компонент (Principal Component Analysis, PCA) [3] – это метод линейного уменьшения размерности, который работает путем встраивания данных с более высокой размерностью в подпространство с более низкой размерностью. Основная идея метода главных компонент состоит в том, чтобы выразить исходные данные в терминах нового набора некоррелированных ортогональных базисных векторов, называемых главными компонентами. Эти компоненты на самом деле являются собственными векторами ковариационной матрицы исходных данных. После этого преобразования ковариация между каждой парой новых компонент становится равной нулю, то есть отделяется влияние одного признака на другие. Причина, по которой метод главных компонент можно использовать для сокращения размерности, заключается в том, что компоненты с более высоким рангом являются направлениями, в которых данные показывают наибольшую дисперсию. Можно было бы просто выбрать некоторые из наиболее важных компонент метода, которые достаточны для объяснения данных для обучения моделей.
Пусть x1, x2,..., xn – исходный набор данных в D-мерном пространстве. Цель метода состоит в том, чтобы представить набор данных в подпространстве W, где W < D [3]. yi как линейная комбинация переменных с i = 1…n определена следующим образом:
yi = AT(x – mx), (1)
где A = |α1||α2|…|αn| – матрица со столбцами, имеющими собственные векторы ковариации исходных данных более высокой размерности, mx – среднее значение исходного набора данных.
Более современные нелинейные методы пытаются сохранить локальные свойства наборов данных более «мягким» способом. В частности, метод SNE (Stochastic Neighborhood Embedding, рус. стохастическое вложение соседей) был разработан для сохранения идентичности соседства [4]. Для этого используется функция стоимости, которая способствует тому, чтобы распределения вероятностей точек, принадлежащих окрестностям других точек, были подобными в многомерном пространстве и в его вложении малой размерности. В первоначальной формулировке для измерения этого сходства использовалось расстояние Кульбака – Лейблера. Более подробно сначала оценивается вероятность того, что выборка xi в многомерном пространстве выберет выборку xj в качестве соседа:
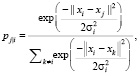 (2)
(2)
где σi – среднее стандартное отклонение с центром в xi.
Точно так же моделируется вероятность того, что yi, аналог xi в пространстве малой размерности, примет yj в качестве соседа:
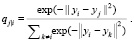 (3)
(3)
Расположение точек yi в пространстве малой размерности определяется минимизацией расстояния Кульбака – Лейблера распределения Q от распределения P:
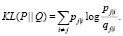 (4)
(4)
t-SNE предлагает функцию стоимости, вдохновленную SNE, но использующую t-распределение Стьюдента, а не распределение Гаусса, чтобы вычислить сходство между двумя точками в пространстве малой размерности. Это распределение значительно облегчает так называемую проблему «скученности», наблюдаемую в SNE, когда удаленные выборки данных, например области с низкой плотностью между естественными кластерами, сближаются в пространстве малой размерности. Кроме того, t-SNE фактически использует симметричную версию SNE, в отличие от первоначальной формулировки, где pj|i не обязательно было равно pi|j. Минимизация функции стоимости выполняется с использованием метода градиентного спуска.
Метод t-SNE [3] хорош преимущественно тем, что он сохраняет метрику. Недостаток метода заключается в том, что, в отличие от PCA, он не является воспроизводимым, то есть его необходимо обучать заново для каждой новой выборки. Главным достоинством PCA является меньшая вычислительная сложность: O(n2m + n3) по сравнению с O(m2n) для метода t-SNE, где m – число точек.
Результаты исследования и их обсуждение
Если выразить исходные данные в терминах собственных векторов, верхние компоненты будут полезны для различения различных классов. Оказывается, что компоненты более низкого ранга, которые выглядят как шумы, могут не предоставлять никакой полезной информации.
При приближении компоненты с более низким рангом также выглядят как шум. Самые низкоранговые компоненты состоят в основном из пикселей по краям в исходном пространстве, от которых необходимо избавиться.
Можно использовать кросс-валидацию для определения количества используемых компонент. В рамках исследования между собой сравнивались пять разных классификаторов из библиотеки sklearn со всеми гиперпараметрами по умолчанию (логистическая регрессия, случайные леса, метод k-ближайших соседей, метод опорных векторов, нейронная сеть). Кроме того, использовалось отбеливание – это способ отбора компонент с наибольшим вкладом в дисперсию. Без отбеливания каждая точка данных имеет очень низкую величину и равномерное распределение в компоненте низкого ранга. То есть эта компонента может быть в основном шумом. Однако после отбеливания размеры вдоль этого направления были расширены.
На рис. 1 приводятся графики результатов для метода главных компонент с отбеливанием и без. Несколько интересных наблюдений:
1. Можно достичь примерно 97 % точности, используя параметры по умолчанию для метода опорных векторов и нейронной сети.
2. Наилучшие показатели достигли максимума в 30–50 компонентах (за исключением логистической регрессии).
3. Использование слишком большого количества компонент приводит к более низким показателям (особенно низким для метода k-ближайших соседей).
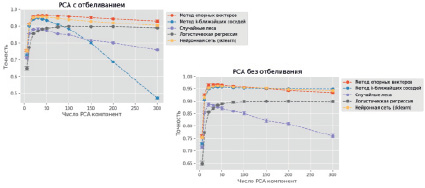
Рис. 1. Результаты точности классификации рукописных цифр с понижением размерности методом главных компонент с отбеливанием и без
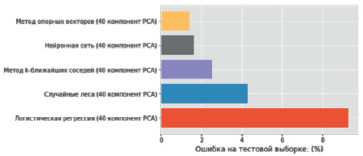
Рис. 2. Результаты ошибки классификации рукописных цифр для различных методов машинного обучения с 40 главными компонентами
На рис. 2 приведены диаграммы результатов распознавания для рассматриваемой задачи. Полученные результаты демонстрируют преимущество методов сокращения размерности в задачах классификации. Имея только 40 главных компонент, можно получить процент ошибок, сопоставимый или даже меньший, чем тот, который был получен при использовании 784 оригинальных признаков. Лучшие результаты на 40 компонентах демонстрирует метод опорных векторов.
Для сравнения сюда могут быть также включены результаты сверточной нейронной сети, которая, как известно [5], является наиболее мощным методом классификации для распознавания изображений. Сверточные нейронные сети учитывают информацию о связанных пикселях (в отличие от других методов, которые рассматривают каждый пиксель как отдельный признак) [6]. Поэтому, как правило, получается гораздо лучшая точность (из-за этого метод главных компонент не применяется к сверточным нейронным сетям). Результаты приведены на рис. 3.
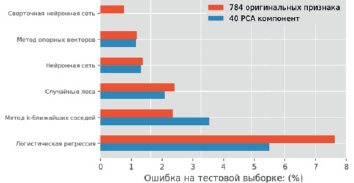
Рис. 3. Результаты ошибки классификации рукописных цифр для различных методов машинного обучения с 40 главными компонентами и 784 оригинальными признаками. Метол главных компонент демонстрирует преимущество в точности классификации
Метод главных компонент часто используется в качестве процедуры предварительной обработки, чтобы уменьшить количество признаков перед выполнением t-SNE. Когда исходные данные встраиваются в двумерную карту t-SNE, то видно, что разные цифры могут быть достаточно хорошо разделены на разные кластеры. Это означает, что можно достичь высокой точности классификации для этого набора данных.
Следующие эксперименты (рис. 4) показывают, что можно получить очень разные карты, даже если более 90 % данных совпадают:
1) заменив 5 % экземпляров на новые в том же случайном состоянии;
2) используя те же данные, но с другим случайным состоянием в алгоритме;
3) добавив 10 % новых экземпляров в том же случайном состоянии.
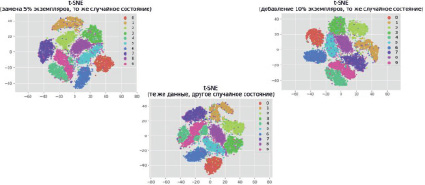
Рис. 4. Результаты экспериментов с недетерминированностью и числом признаков t-SNE
Метод t-SNE в основном используется для визуализации данных, а не для классификации. Хотя он может создавать красивые двумерные карты кластеризации, он часто нецелесообразен для прогнозирования новых входных данных по двум причинам:
1. Чтобы t-SNE работал, нужно одновременно подавать все данные в алгоритм.
2. Во время подготовки к обучению есть некоторая хаотичность. Даже если будут переданы одни и те же данные в один и тот же алгоритм, выходная карта может отличаться.
Поэтому, если требуется классифицировать новые входные данные, необходимо объединить их с предыдущим набором и заново обучить всю модель.
Что может сказать t-SNE, так это то, насколько отделимым является набор данных. В ситуации, когда удается хорошо визуализировать данные с помощью t-SNE с низкой точностью классификации, необходимо повторно выбрать методы классификации / гиперпараметры и используемую обработку данных и попытаться найти потенциальное улучшение.
Заключение
Используя метод PCA, можно уменьшить количество признаков для обучения некоторых моделей с 784 до 40 и достичь схожей или даже более высокой точности. Время выполнения для классификации значительно сокращается с помощью методов сокращения размерности.
Отбеливание после преобразования PCA не является необходимым для этого набора данных, и это может привести к снижению точности для метода k-ближайших соседей.
Получаемые тестовые ошибки сопоставимы с эталоном. Например, ошибка на тестовой выборке в 1,6 % так же хороша, как и вероятность, которую можно получить для MNIST с методом опорных векторов. Чтобы получить еще более низкий уровень ошибок, требуется дополнительная обработка данных с устранением перекосов / искажений в сочетании с более сложными моделями.
В заключение стоит отметить, что сокращение размерности может быть очень полезным для задач классификации при стремлении к сокращению времени вычислений и увеличению точности. Точный метод и дополнительная обработка зависят от набора данных и задачи, и, конечно, от классификаторов. Нужно внимательно изучить характер данных и выбрать правильную комбинацию.

