Эффект безлинзового формирования изображений периодических структур впервые был зарегистрирован Тальботом в 1836 г. [1]. В современных исследованиях рассмотрены различные аспекты явления формирования саморепродукций периодическими объектами.
Рассмотрение условий возникновения явления саморепродуцирования в предельно общем случае косоугольной элементарной ячейки, заключающей произвольный по функции прозрачности объект, дано в [2–4]. Для описания транспаранта, состоящего из ячеек подобного типа, авторы исходили из того, что ряд Фурье определенной в ограниченном интервале функции, вне области ее определения, дает бесконечное количество регулярных повторений этой функции. То есть ряд Фурье ведет себя как оператор размножения. Используя это свойство ряда Фурье, можно описать пространственно-регулярный двумерный транспарант, состоящий из бесконечной совокупности идентичных прямоугольных ячеек.
Явление саморепродуцирования при наклонном освещении рассмотрено в [5]. В работе исследованы закономерности формирования дифракционных картин за одномерными и двумерными периодическими транспарантами, освещенными наклонным пучком когерентного света. Выяснены условия наблюдения явления саморепродуцирования на объектах конечного размера.
В работах [6–8] с общих позиций теории образования изображений при когерентном и некогерентном освещении рассмотрен процесс образования изображения в явлении саморепродуцирования при освещении объекта излучением с модулированной пространственной когерентностью. Модуляция пространственной когерентности позволяет использовать излучение от широкофокусных источников с широким спектром. Сообщается о результатах по наблюдению фурье-изображений в мягком рентгеновском излучении, полученном с помощью источника синхротронного излучения. Рассмотрены дисперсионные свойства явления саморепродуцирования. Приведены экспериментальные результаты и расчетные кривые спектрометрических исследований.
Явление саморепродуцирования обычно наблюдают при освещении решетки плоской волной, т.е. при падении на решетку коллимированного пучка света. Исследование явления саморепродукции в случае произвольного волнового фронта проведено в [9, 10]. Получены обобщенные решения на базе дифракционной теории в приближении Френеля. Подробно исследован случай гауссиановского пучка. Показано, что типичный пример явления саморепродуцирования существует и в этом случае.
Важным моментом в исследованиях явления саморепродуцирования является учет влияния различных фазовых сред на распределение саморепродукций.
Целью данной работы является анализ воздействия некоторых простейших фазовых сред на распределение плоскостей саморепродукций линейной решетки.
Последовательность саморепродукций в простейших фазовых средах
Рассмотрим простейшие фазовые среды, такие как оптический клин и тонкая линза. Для оптического клина фазовые возмущения светового поля можно представить в виде [11, 12]
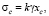где 
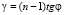, (1)
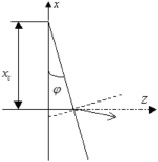
Схема возникновения фазовых искажений при прохождении световой волны сквозь оптический клин
здесь φ – угол при вершине тонкого клина (рисунок). Важно отметить, что для тонкого клина выполняется следующее важное условие: угол при вершине настолько мал, что можно воспользоваться приближением малых углов. Такое приближение позволяет сильно упростить вычисления, при этом практически не воздействуя на общность задачи.
Световое поле после оптического клина имеет вид
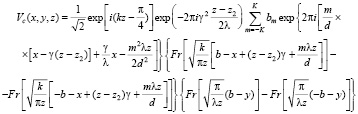. (2)
Соотношение (2) показывает, что оптический клин осуществляет смещение вдоль направления оси x последовательности саморепродукций, которая формируется световым полем. Помимо этого плоскость восстановления разворачивается на угол γ. Переход к системе координат, которая повернута на угол γ относительно оси, позволяет преобразовать картину восстановления, формируемую световым полем, к картине, формируемой световым полем в отсутствии оптического клина.
Далее рассмотрим объект типа тонкая линза [13] в качестве объекта, вносящего фазовые возмущения в последовательность саморепродукций. В соответствии с [14, 15] фазовое воздействие, осуществляемое тонкой линзой, можно записать в следующем виде:
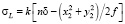, (3)
здесь δ – толщина линзы вдоль её оптической оси, f – фокусное расстояние линзы. Световое поле за тонкой линзой можно записать в следующем виде:
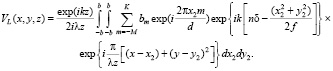(4)
Рассмотрим интеграл (4) как преобразование Фурье:
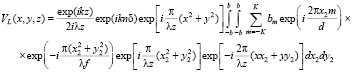. (5)
После внесения интеграла под знак суммирования получаем
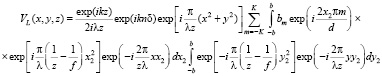. (6)
Перейдем к интегралу по переменной y2. Изменим этот интеграл с целью упрощения, сделав замену следующим образом:
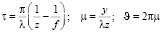. (7)
Представим этот интеграл, обозначив его буквой D, в следующем виде:
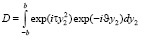. (8)
Интеграл (8) можно представить в виде
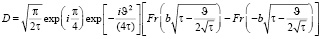. (9)
Возвращаясь к начальным переменным, имеем следующее соотношение:
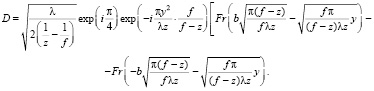(10)
В случае интеграла по переменной x2, принимая во внимание то, что в данном случае мы реализуем Фурье-преобразование функции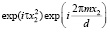 
, выражение для результата интегрирования получаем в следующем виде:
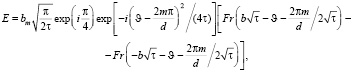(11)
где τ, μ,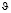 
такие же, как и в (7).
После возврата к начальным переменным имеем следующее выражение для E:
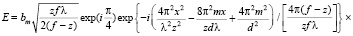
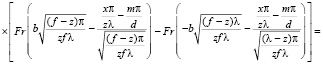
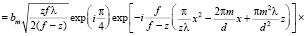
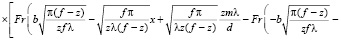
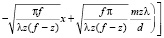. (12)
Введем новые переменные
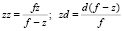. (13)
Окончательное выражение для значения интеграла (6) имеет вид
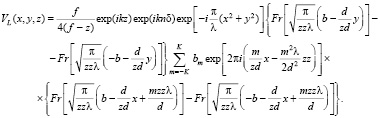(14)
Из (14) можно видеть, что для светового поля распределение за линзой подобно распределению поля в отсутствии линзы, однако период саморепродуцирования светового поля в рассматриваемом случае задается выражением (13) для zd.
Обозначив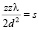 
, можно представить соотношение для определения плоскостей саморепродукции в следующем виде:
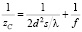. (15)
Из выражения (15) видно, что плоскости саморепродукции сгущаются перед фокальной плоскостью и разрежаются за ней. Масштаб саморепродукций подчиняется соотношению (13) для zd. Из (13) видно, что перед фокальной плоскостью размеры саморепродукций уменьшаются, а за ней возрастают.
Выводы
Рассмотрены фазовые среды типа оптический клин и тонкая линза. Показано, что оптический клин осуществляет смещение вдоль направления оси x последовательности саморепродукций, которая формируется световым полем. Помимо этого плоскость восстановления разворачивается на некоторый угол γ. Переход к системе координат, которая повернута на угол γ относительно исходной оси, позволяет преобразовать картину восстановления, формируемую световым полем, к картине, формируемой световым полем в отсутствии оптического клина.
Для объекта типа тонкая линза аналитически показано, что для светового поля распределение за линзой подобно распределению поля в отсутствии линзы, но при этом плоскости саморепродукции сгущаются перед фокальной плоскостью и разрежаются за ней. Кроме того, перед фокальной плоскостью размеры саморепродукций уменьшаются, а за ней возрастают.