Результаты экспериментов Майкельсона по измерению скорости света трактуются как экспериментальное подтверждение специальной теории относительности, они широко известны и представляют актуальный предмет обсуждения свыше ста лет с момента проведения. Эксперименты были поставлены, чтобы обнаружить отставание эфира от орбитального движения Земли и от суточного вращения ее поверхности. Для измерения скорости света использовался сконструированный Майкельсоном интерферометр. Когерентность волн в нем обеспечивало деление входного луча света на два луча, которые распространялись прямолинейно под прямым углом друг к другу, затем зеркально отражались обратно. Через полупрозрачное зеркало разделённые лучи направлялись на экран, где интерферировали. Числовая обработка параметров интерференционной картины с учетом влияния компонентов конструкции позволяла сравнительно точно на момент проведения эксперимента определить скорость света. Предполагалось, что несущая свет среда эфира отстает от движения Земли, поэтому свет покажет различные интерференционные картины при движении луча в прямом и обратном направлении. Опыт дал нулевой эффект: картины в обоих случаях оказались одинаковыми в соответствии равным скоростям света в противоположных направлениях. Было принято теоретическое объяснение, состоявшее в том, что среда эфира не существует. Однако не исключено и другое – гипотетическая среда движется вместе с Землей, что соответствовало бы тем же результатам эксперимента. В эксперименте Майкельсона – Морли интерферометр имел повышенную чувствительность, несущая конструкция могла поворачиваться по всем горизонтальным направлениям. При любом направлении луча света скорость распространения оказывалась равной скорости распространения в обратном направлении. Предположение об отсутствии материальной среды распространения света получало дополнительное экспериментальное подтверждение. Однако допустимо предположить, что среда движется вместе с Землей не только в орбитальном направлении, но и сопровождает вращение Земли вокруг оси, что в равной мере соответствовало бы результатам экспериментов. Сопровождающее движение среды, предположительно, следствие гравитационного притяжения Земли и всей массы вращающейся земной материи. Напротив, если масса платформы на поверхности Земли невелика, то ее гравитационное притяжение не увлекает за собой среду: сложение сил притяжения Земли и платформы сохранит направление притяжения только к Земле. Такое объяснение можно предполагать для эффекта эксперимента Саньяка. В эксперименте разделенный надвое луч света обегал с помощью зеркал кольцевой периметр платформы во встречных направлениях и собирался на экране в интерференционную картину. Пока платформа была неподвижной, интерференционные полосы оставались одинаковыми, когда платформа приводилась во вращение, полосы расходились. Саньяк трактовал эффект как отставание среды распространения света от поверхности вращения. Майкельсон неоднократно воспроизводил этот опыт и признавался, что если бы сначала выполнил этот эксперимент, то считал бы, что среда эфира существует и отстает от локального движения тел.
Статья посвящена определению условий, при которых результаты экспериментов Майкельсона, Майкельсона – Морли и Саньяка могли бы однозначно объясняться наличием, а не отсутствием материальной среды передачи электромагнитных волн.
Цель исследования – привести расчеты, показывающие, что из результатов данных экспериментов не следует отрицание материальной среды вакуумного пространства как среды распространения электромагнитных волн, а следует лишь отрицание ее абсолютной неподвижности. Вычисления опираются на предположение близкодействия, механизм которого связывает материю вакуума с веществом, электромагнетизмом и гравитацией. На этой основе требуется представить численные соотношения взаимодействия гравитационного поля с материей вакуумного пространства, из которых следует движение среды вакуумного пространства вместе с локальным источником гравитации, что служило бы единым объяснением, казалось бы, противоречащих друг другу результатов экспериментов.
Гипотеза близкодействия
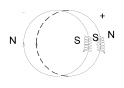
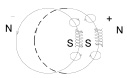
Необходимое для дальнейшего изложение основной части гипотезы заимствуется из [1], в условиях гипотезы трактуются эффекты классических экспериментов по измерению скорости света. Предполагается, что наименьшим физическим элементом близкодействия электрического и магнитного полей, а также поля гравитации является устойчивая вращающаяся электрон-позитронная пара. Электрон в паре представляет собой замкнутый тороидальный вихрь, направленный вдоль окружности как оси вращения. Предполагается, что в данном состоянии электрон обладает свойством кругового витка постоянного тока и имеет два противоположных магнитных полюса. Позитрон в паре находится в аналогичном состоянии с такими же двумя магнитными полюсами. Оба вихря механически вращаются в одинаковом направлении с одинаковой скоростью в параллельных плоскостях, расстояние между которыми соизмеримо с радиусом оси вращения (рис. 1, а). Предполагается, что в этом случае оба вихря сохраняют свойства электрических токов взаимно противоположного направления (рис. 1, б), поэтому обращены друг к другу одноименными магнитными полюсами. Вращение в паре предполагается абсолютно устойчивым (как при сверхпроводимости – в вакууме нет сопротивления), электрон и позитрон сохраняют постоянные единичные заряды противоположного знака и поэтому взаимно притягиваются. Одноименная магнитная полярность на обращенных друг к другу сторонах круговых витков исключает критическое сближение, как следствие исключена возможность аннигиляции в паре.
а)
б)
Рис. 1. Расположение магнитных полюсов в вихревой электрон-позитронной паре, механическая винтовая (а) и электрическая (б) ориентация вихревых витков на взаимное отталкивание
Предполагается также, что в силу вихревой природы вращения каждый компонент пары имеет винтовые вихревые витки, которые в компонентах пары ориентированы во взаимно противоположном направлении. С учетом знака заряда это приводит к противоположности направлений элементов их токов на обращенных друг к другу сторонах компонентов пары (рис. 1). Такие вихревые витки создают локальные изменения магнитного поля, ориентированные на взаимное отталкивание компонентов пары, что дополнительно противодействует возникновению аннигиляции. Следующее предположение заключается в том, что компоненты электрон-позитронной пары обладают свойством электрических токов в макроскопических проводниках, а именно электромагнитной индукцией. При этом взаимная индукция препятствует любому изменению локальных элементов магнитных полей круговых и вихревых токов компонентов пары. Именно данное свойство обеспечивает устойчивость состояния электрон-позитронной пары, благодаря которому компоненты среднестатистически остаются на одном и том же расстоянии друг от друга, сохраняют размеры и форму. Однако это так только при отсутствии внешнего электромагнитного возмущения, наличие которого может влиять на геометрические, пространственные и физические параметры компонентов пары. Необходимо учесть особенности гипотетических электрон-позитронных пар, относящиеся к их взаимодействию с внешними объектами. Они имеют диаметр существенно меньший диаметра свободного электрона. Это следует из того, что равнодействующая винтовых вихревых витков электрона (аналогично, позитрона) всегда направлена к центру оси вращения [2], в результате замкнутый тороидальный вихрь должен оказаться сжатым до «точечных» размеров. На сравнительно удалённом расстоянии пара воспринимается как электрически нейтральная (противоположные заряды складываются в «одной точке» в нулевое действие). На аналогичном расстоянии пара воспринимается как немагнитный объект (две пары противоположных магнитных полюсов сконцентрированы в «одной точке»). Поэтому рассматриваемый объект микромира нейтрален по отношению к любому заряженному и намагниченному объекту, находящемуся на относительном удалении. Так, сдвоенный замкнутый электрон-позитронный вихрь должен восприниматься как электрически и магнитно нейтральный объект в межатомном и межмолекулярном пространстве, тем более – на макроскопическом от него расстоянии. Поэтому он не обнаруживает себя в известных взаимодействиях микро- и макромира. Принципиальное для дальнейшего предположение заключается в том, что рассматриваемые электрон-позитронные пары заполняют все вакуумное пространство вселенной, а также все свободное межатомное пространство вещества, где обладают «неограниченной» проникающей способностью. Нейтральные в макроскопическом измерении точечные заряды и магнитные полюса элементов приводят к физическому восприятию вакуума как пустоты без физических объектов и свойств. Возможность аннигиляции различных пар исключена тем, что все пары обращены друг к другу только одноименными магнитными полюсами: те пары, у которых вовне были обращены взаимно противоположные полюса, аннигилировали, их не осталось в пространстве вакуума. Несмотря на взаимную нейтральность, на достаточно малом расстоянии друг от друга вихревые электрон-позитронные пары могут определять взаимную пространственную ориентацию. Кроме того, их взаимную пространственную ориентацию, от элемента к элементу, определяет также заряд достаточно близко расположенного ядра атома и его магнитное поле, аналогично заряд и магнитное поле макроскопического физического тела. Непосредственно ниже предположение об электрон-позитронной структуре вакуума c видоизменением распространяется на структуру нуклонов атомного ядра, что влечет гипотетическую связь гравитации и электромагнетизма. Отсюда будет вытекать, что гравитационное поле атомов и макроскопических тел оказывает влияние на взаимное положение и пространственную ориентацию электрон-позитронных пар вакуума посредством передачи действия от элемента к элементу. Именно, предполагается, что нуклоны состоят из таких же вихревых электрон-позитронных пар, которые заполняют вакуумное пространство. В силу симметрии действия на элементы вакуума нуклон имеет шарообразную форму, замкнутые вихревые пары располагаются равномерно по его сферической поверхности (рис. 2). Пусть вначале рассматривается нейтрон. Его электрическую нейтральность обусловливает следующая особенность структуры. Перпендикулярные плоскостям вращения оси электрон-позитронных пар нейтрона попарно повернуты друг относительно друга на ≈180°, чередуя на внешней стороне поверхности заряды + и – в порядке клеток шахматной доски:
(1)
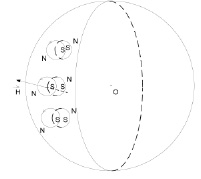
Рис. 2. Магнитная ориентация электрон-позитронных пар на сфере нуклона
Под каждым +из (1), расположенным на внешней стороне поверхности нейтрона, с внутренней стороны этой поверхности, вдоль оси электрон-позитронной пары, располагается сдвоенный с ним –, и аналогично под каждым – располагается сдвоенный с ним +. Оси располагаются радиально к центру нейтрона. Пары удерживаются на поверхности взаимным притяжением электрических зарядов, а также винтовых вихревых витков, которые в данном расположении направлены на притяжение на участках «касания». Кроме того, замкнутые вихревые пары попарно чередуют смещение вдоль осей к центру нейтрона и обратно, усиливая взаимное притяжение за счет смещения внешних магнитных полюсов соседних пар к внутренним, им противоположным. Предполагается, что протон возникает из нейтрона вследствие того, что чередование (1) в окрестности некоторой точки поверхности нейтрона является однократно нарушенным относительно расположения отрицательных зарядов:
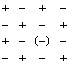(2)
Соседние отрицательные заряды выталкивают лишний «внутренний» между ними заряд (–), восстанавливая расположение (1). Но тогда на поверхности остается не скомпенсированный позитрон с зарядом (+) в состоянии устойчивого замкнутого вихря. В результате нейтрон распадается на протон и электрон, протон остается с зарядом позитрона, по модулю равным заряду электрона. Эта реакция известна как β-распад: в свободном состоянии нейтрон распадается на протон, электрон и электронное антинейтрино: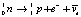 
. После распада протон остается в абсолютно устойчивом состоянии.
Можно допустить, что в ядре атома образовавшийся заряд протона (+), будучи не скомпенсированным, ориентируется на зону отрицательного участка поверхности нейтрона вокруг (–), как иллюстрирует (2). Все вместе это влечет особенности ядра, на основе которых объяснимо равенство модулей зарядов протона и электрона, происхождение орбитальных электронов атома, равенство их количества числу протонов ядра, наглядно объясняется естественная радиоактивность, с некоторыми оговорками – искусственная радиоактивность. Данные аспекты детализируются в [2], ниже они не обсуждаются.
Принимается, что нуклоны ядра с описанной гипотетической структурой в непосредственной близости от себя ориентируют замкнутые вихревые электрон-позитронные пары пространства. На поверхности нуклона присутствуют магнитные полюса одного типа (внешние полюса замкнутых вихревых пар). Пусть условно это полюса N (рис. 2). В этом случае ближайшая к полюсу N замкнутая вихревая пара пространства повернется сдвоенным внутренним полюсом S. В свою очередь, к ее сдвоенному полюсу S соседняя с ней пара повернется полюсом N. В продолжение процесса получится цепочка вида
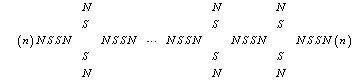(3)
В скобках обозначено положение начального и конечного нуклона атомов двух тел, между которыми протянулась цепочка замкнутых сдвоенных вихрей. Изображение (3) условно. На самом деле в промежутках между ортогональными комбинациями полюсов может оказаться не одна комбинация полюсов вихревой пары NSSN, а несколько таких последовательных комбинаций – по причине взаимной ориентации согласно зарядам по схеме
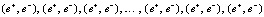(4)
(так ориентированы элементы силовых линий стационарных электрических зарядов противоположного знака [1]). Если эти заряды справа от ортогональной комбинации заканчивались знаком +, то наиболее вероятно, что слева цепочка продолжится знаком – вследствие притяжения противоположных зарядов. Однако притяжение зарядов ослаблено расстоянием, и не исключено, что комбинация полюсов NSSN развернется на 180°. Это означает, что продольные элементы цепочки могут иметь различную ориентацию зарядов, комбинируемых по типу (4). В результате сила, с которой действует один элемент цепочки на конечный объект, будет существенно слабее (ввиду частичного противодействия промежуточных элементов), чем это было в случае кулоновского взаимодействия [1]. У протона образуются аналогичные цепочки, но среди них могут быть и те, которые начинаются с продольной (а не ортогональной) комбинации NSSN, по причине наличия у него заряда +. В дальнейшем своем продолжении цепочки примут вид, аналогичный (3). Можно заметить, что расположение вдоль поверхности нуклона точечных комбинаций полюсов вида NSSN (рис. 2) делает нуклон объектом со скомпенсированным магнетизмом для относительно удаленных физических тел.
Пусть вначале принимается предположение, что действие гравитационного притяжения одного тела на другое передается вдоль силовой линии от ее элемента к ее элементу (в дальнейшем будет оговариваться, что в передаче действия участвуют также элементы среды вакуумного пространства, окружающей силовые линии). За продольную ось силовой линии гравитации точечного тела принимается комбинация замкнутых тороидальных вихревых электрон-позитронных пар, образующих цепочку вида (3). В среде вакуумного пространства у цепочки вида (3), входящей в силовую линию, есть ответвления, продолжающие ортогональные комбинации полюсов, которые в своем продолжении также имеют ответвления. Поэтому силовые линии гравитационного поля имеют древовидную структуру. В целом, как и в случае электростатических силовых линий [1], элемент силовой линии гравитации состоит из хаотичного набора подвижных замкнутых электрон-позитронных вихрей, в котором доминирующая магнитная ориентация соответствует (3). В стационарном состоянии действие всегда направлено на взаимное притяжение элементов, а суммарное действие – на притяжение начального и конечного объектов. Вероятность нахождения любого элемента силовой линии в положении из (3) в каждый момент времени больше 2–1.
Ниже, пока не оговорено иное, силовая линия поля понимается как линия движения пробного тела под действием элементов среды.
Аналогично, как отмечалось, в соответствии с (4), определяется силовая линия электрического заряда [1]. Наименьшие физические элементы силовых линий статического электричества и гравитации в данных предположениях одни и те же, механизм передачи действия от элемента к элементу сохраняется, передача действия в этих двух полях, с означенными оговорками, различается количественно – в конечной оценке – значениями коэффициентов пропорции. Поскольку речь идет о действии элемента на элемент, то в количественном выражении такого действия должно предполагаться наличие инертной массы элемента. Это обстоятельство требует различать между сколь угодно малым элементом вакуума в макроскопическом измерении и минимальным физическим элементом микромира вакуума – замкнутой вихревой электрон-позитронной парой. Требуемое различие проводится в дальнейшем по ходу обсуждения действия гравитации на физические тела и на вакуум.
Всюду ниже, если не оговорено иное, синоним «электрон-позитронная пара» понимается только как рассмотренная выше замкнутая вихревая электрон-позитронная пара.
Интерпретация закона всемирного тяготения в аспекте близкодействия
Пусть даны два точечных тела массой M и m, расположенных в центрах o и o1, на макроскопическом расстоянии R друг от друга. Пусть сила взаимного притяжения их компонентов единичной массы обозначена f. Вначале модель близкодействия рассматривается в упрощенной форме. Принимается, что все силовые линии двух рассматриваемых тел замкнуты и попарно симметричны относительно линии центров oo1. Симметричные элементы, понимаемые как векторные элементы действия (но не наименьшие физические элементы), проектируются на отрезок oo1, сумма их попарно симметричных проекций по направлениям соответствует (3). Проекции векторов обратных направлений взаимно уничтожаются с проекциями векторов продолжений таких силовых линий до перпендикулярных границ линии центров. В результате любой сколь угодно малый элемент действия суммы проекций всех силовых линий направлен в соответствии с (3). Элемент силовой линии (не элемент действия) здесь понимается как множество электрон-позитронных пар, заключенных в сколь угодно малом объеме пространства, взятом в макроскопическом измерении.
Действие передается от одного элемента к другому, при этом передача действия на конечное тело может терять силу на каждом передаточном элементе вследствие колебаний взаимной ориентации электрон-позитронных пар. Более точно, действие точечного тела передается на ближайший к нему элемент силовой линии, тот в свою очередь передает это действие на следующий элемент, при этом в процессе передачи элемент может потерять часть переданной ему силы, вместе с тем присоединит к ослабленному действию силу своего собственного притяжения к ближайшему элементу. Такой механизм воспроизводится в продольном направлении силовой линии до окончательной передачи действия тела массой M вместе с действием всех промежуточных элементов силовой линии телу массой m.
За элемент действия тела единичной массы в составе M на тело единичной массы в составе m на расстоянии r от первого принимается полностью переданное действие на второе тело от элемента суммы действий, спроектированных на линию центров oo1 силовых линий, находящегося на расстоянии r от точки o. Абсолютная величина элемента действия обозначается df, где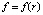 
.
Полное рассматриваемое действие определяется как интегральная сумма элементов действий. При описании интегрального суммирования термин «элемент» понимается только в макроскопическом измерении.
Как гипотеза принимается, что элемент действия обратно пропорционален кубу расстояния с экспоненциальным весом. Более точно предполагается, что абсолютная величина элемента действия тела единичной массы в составе M на тело единичной массы в составе m, в случае если элемент действия находится на расстоянии r от первого тела, может быть представлена дифференциалом
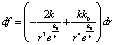, (5)
где k, k0 – некоторые постоянные (согласуемые в дальнейшем с законом всемирного тяготения), или
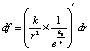. (6)
Физически действие передается от одной электрон-позитронной пары к другой вдоль цепочки вида (3), через физически наименьшие элементы силовых линий, в то время как дифференциал (5) – сколь угодно малая величина в макроскопическом измерении. Он выражает модуль действия множества физически наименьших элементов – электрон-позитронных пар, – обладающих суммарной ориентацией в соответствии с (3), заключенных в сколь угодно малых объемах пространства в макроскопическом измерении, взятых вокруг проектируемых на линию центров точек силовых линий. Формально дифференциал выражает модуль суммы проекций элементов действий вдоль силовых линий на отрезок длины dr на линии центров. Дифференциал – модуль элемента интегральной суммы. Действие этого интегрального элемента складывается во взаимное притяжение с любым таким же элементом в соответствии с суммарной ориентацией составляющих физически наименьших элементов.
В предположении относительно (5) целесообразно абстрагироваться от конкретного описания (исключительного значения) силовых линий. В самом деле, окружающие силовые линии элементы среды вакуумного пространства, состоящие из электрон-позитронных пар, ориентируются на элементы цепочек вида (3), следовательно, они взаимодействуют с ними и участвуют в передаче гравитационного действия одного тела на другое. Соответствующие элементам векторы сил складываются таким образом, что вектор их полной суммы коллинеарен цепочке (3) и направлен только на притяжение одного тела к другому. В макроскопическом измерении силовые линии заполняют пространство непрерывно, сливаясь друг с другом. Они разделяются в измерении микромира, где между ними образуются расстояния, соизмеримые с расстояниями между ядрами атомов, нуклоны которых порождают их продольные оси – цепочки вида (3).
Искомое предположение можно сформулировать в следующем виде. Для двух рассматриваемых макроскопических тел с центрами o и o1 на расстоянии R друг от друга элементы силовых линий и окружающей их вакуумной среды пространства ориентируются и взаимодействуют таким образом, что дифференциал, понимаемый в макроскопическом измерении, взятый от проекции суммы действий всего множества таких элементов на линию центров oo1 на расстоянии r < R от точки o, по абсолютной величине выражается из (5).
Согласно (5) абсолютная величина силы действия тела единичной массы в составе M (включающая действия окружающих элементов силовых линий) на тело единичной массы в составе m на расстоянии R между ними выразится как интеграл
.
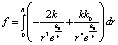Отсюда, с учетом (6),
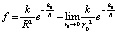. (7)
В (7) предельное вычитаемое равно нулю. Таким образом,
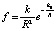. (8)
Из разложения экспоненты в ряд Лорана
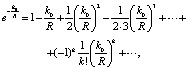(9)
с учетом чередования знаков членов сходящегося ряда (при условии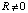 
), получится, что модуль разности между силой притяжения тел с единичной массой по закону всемирного тяготения (fN) в канонической форме и выражением (8) (при условии k = γ) составит
.
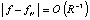Из (8), (9) следует представление силы гравитационного притяжения в виде
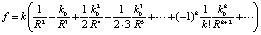, (10)
или
.
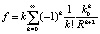Согласно теореме Лейбница об остатке сходящегося знакопеременного ряда из (10), в частности, следует
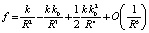. (11)
Появление весового множителя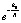 
в (8) обусловлено спецификой модели, в рамках которой выполняется вывод формулы (8). Если этот множитель не вводить, то интегральное суммирование вдоль линии центров повлечет бесконечное значение вычитаемого предела в (7). С другой стороны, формальное наличие весового множителя 
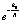может отражать физическую (статистическую) закономерность убывания силы действия элемента на расстоянии R в (5) и (6). Имеет значение также то, что наличие веса 
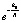в (8) избавляет закон обратных квадратов от некорректности при R = 0. Закон всемирного тяготения
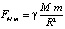(12)
дает бесконечное значение силы притяжения при R = 0 для любых двух тел с ненулевой массо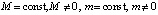й (
, и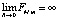 
), что противоречит наблюдаемому поведению реальных макроскопических тел при их взаимном сближении на нулевое расстояние. Формула (8) в то же время в пределе обращает эту силу в ноль с переходом к физическим параметрам и расстояниям микромира (
).
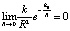Соотношение (8) дано для двух точечных тел с единичной массой. Наличие массы М по построению модели М-кратно увеличивает действие точечного тела с единичной массой в составе M: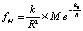 
. Это соответствует М-кратному росту числа нуклонов, каждый из который порождает рассмотренное выше действие. Поскольку fM относится к действию на тело единичной массы, 
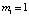, то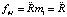 
. Отсюда
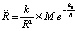. (13)
Обе части равенства (13) можно умножить на массу второго тела m:
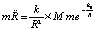, (14)
или
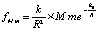. (15)
В равенстве (14) массы m всегда можно сократить, тем самым, согласно (13), ускорение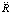 
не зависит от массы тела, которое притягивается к центру гравитации. Если теперь принять k равным гравитационной постоянной γ, то полученное соотношение (15) примет вид аналога (12) с поправкой:
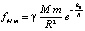. (16)
Поскольку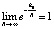 
, то при достаточно больших значениях R множителем 
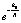можно пренебречь, и выражение (16) перейдет в (12).
Аналог, сходный с соотношением (11), для закона всемирного тяготения рекомендовал использовать Ньютон, использовали Клеро (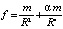
или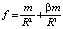 
) и Даламбер с целью вывода из этого закона численных значений смещения перигея орбиты Луны [3]. Непосредственно из канонической формы закона независимо друг от друга Клеро и Даламбер вывели все численные значения особенностей лунной орбиты, определяющиеся известными соотношениями в неравенствах, при этом, однако, смещение перигея получалось более чем вдвое превосходившим наблюдавшееся в астрономии значение, такой же результат получался у Ньютона [3]. Применение аналогичного (11) соотношения при соответственном выборе коэффициентов позволило Клеро и Даламберу дать правильное на тот момент численное значение смещения перигея Луны.
Из (13), (14) следует, что для сколь угодно малого элемента массой md, независимо от этой его массы, выполнено
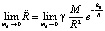
и
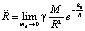. (17)
Согласно (17) закономерность (13) формально сохраняется для элементов не только с любой ненулевой (в том числе сколь угодно малой) массой, но также для материальных элементов с нулевой инертной массой. Однако тот факт, что эта закономерность применима к элементам вакуума, можно лишь предполагать, как и то, что элементы вакуума находятся под действием поля гравитации, создающего у них наряду с веществом центростремительное ускорение (13), где k = γ.
Вместе с тем эти предположения нельзя не сделать: в условиях близкодействия тело массой M передает свое гравитационное действие через элементы вакуума, следовательно, оно взаимодействует с элементами вакуума. При этом оно передает действие, количественно равное (16), действуя с такой же силой на множество элементов вакуума, аккумулирующих и передающих это действие непосредственно на тело массой m.
Абсолютная величина элемента действия df тела единичной массы в составе M на физический элемент, как отмечалось выше, понимается в макроскопическом измерении силы. Но такая сила подчиняется второму закону Ньютона. В этой трактовке элемент силовых линий, как и элемент окружающего их пространства, должен, поскольку он передает действие, обладать инертной массой md, md ≠ 0, при этом действие в макроскопическом измерении (в соответствии с трактовкой дифференциала) сколь угодно мало. Действия всех данных элементов суммируются таким образом, что они эквивалентно передают действие одного тела макроскопической массы другому телу, также обладающему макроскопической массой. С другой стороны, сама по себе электрон-позитронная пара является физически наименьшим элементом силовой линии и окрестного вакуумного пространства. Она заключена в объеме макроскопической «меры нуль», ее масса в макроскопическом измерении абстрактно может предполагаться нулевой. Такие трактовки мер элементов были необходимы в представлении интегральной оценки гравитационного взаимодействия двух тел, элементы «меры нуль» при этом игнорировались.
У физически наименьшего элемента вакуумного пространства (электрон-позитронной пары), существование которого на данный момент лишь предположение, в условиях его абстрактной локальной неподвижности, вопрос о наличии ненулевой инертной массы является открытым. Соответственно, открыт вопрос о наличии или отсутствии инертной массы у элемента вакуума, рассматриваемого в макроскопическом измерении. Поэтому ниже будут рассмотрены два случая: md ≠ 0 и md = 0. В этом аспекте необходимо заметить, что предположение о наличии ненулевой массы у элемента вакуума не является необходимым для вывода формулы (16). Достаточно априори предполагать, что действие от элемента к элементу таково, что вызывает ускорение каждого элемента (каждого элемента силовых линий гравитации и окружающего их вакуумного пространства). Более подробно, дифференциал (5) можно переписать только для ускорения, учитывая, что это выражение составлено для действия тела с единичной массой m1. Тогда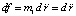 
, и (5) перейдет в соотношение
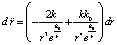. (18)
Именно закономерность для ускорения (18) в этом случае должна априори предполагаться вместо закономерности (5) для силы: для двух рассматриваемых макроскопических тел с центрами o и o1 на расстоянии R друг от друга элементы силовых линий гравитации и окружающего их вакуумного пространства взаимодействуют таким образом, что дифференциал, понимаемый в макроскопическом измерении, взятый от проекции суммы ускорений всего множества таких элементов на линию центров oo1 на расстоянии r < R от точки o, по абсолютной величине выражается из (18).
В (18)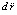 
– элемент модуля ускорения. Модуль полного ускорения определяется как интегральная сумма элементов:
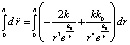. (19)
С учетом соотношения (6), которое в рассматриваемом случае эквивалентно перейдет в соотношение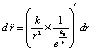 
, получится
.
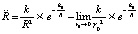Отсюда следует аналог (8) для ускорения:
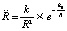. (20)
Для тела массой M вызванное им ускорение тела единичной массы возрастет M-кратно, и (20) соответственно перейдет в соотношение для ускорения: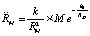 
, индекс M ниже опускается. Умножение обеих частей на значение массы m влечет 
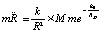, или, 
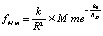. Отсюда следует аналог (16), если принято k = γ. Опираясь на предположение (19) и на следствие из него, (20), можно оценивать значение не силы, действующей на тело, а пользоваться оценкой именно ускорения данного тела. В частности, для притяжения Земли ускорение будет центростремительным с оценкой (20) (k = γ) и не будет зависеть от массы тела m.
Электромагнитные волны в световом спектре согласно предложенной модели распространяются в электрон-позитронной среде пространства. На основе представленных соотношений требуется оценить влияние гравитационного поля Земли на эту среду и на скорость распространения в ней света.
Гравитационное действие на электрон-позитронную среду вблизи земной поверхности и эксперименты по измерению скорости света
Особенность обсуждаемой гипотезы в том, что электрон-позитронные пары окружающего вакуумного пространства предполагаются среднестатистически неподвижными относительно системы отсчета на поверхности Земли. Существование электрон-позитронных пар вакуума предполагала «дырочная» теория П. Дирака [4] (с поправкой Г. Вейля), однако без предположений о каком-либо локальном перемещении пар (и без предположений о структуре их взаимного расположения). В развитие теории Дирак опубликовал исследования относительно волновой природы рассматриваемых частиц [5]. В обоих случаях вакуум трактовался как особое состояние материи, которое не наблюдаемо по аналогии с представлениями квантовой теории химической валентности. Существует сравнительно много фактов, косвенно указывающих на электрон-позитронную структуру вакуума, число таких фактов, как представляется, неуклонно растет. В частности, можно отметить теоретические и экспериментальные исследования по рождению электрон-позитронных пар непосредственно из вакуума [6–8].
Отличие предложенной гипотезы от квантово-механических концепций волнового дуализма элементарных частиц [9] принципиально. Возможно, оно отчасти нивелируется в границах следующей краткой трактовки волновых и корпускулярных явлений. Электрон-позитронные пары вакуума в сравнительно малой окрестности каждого небесного тела большой массы среднестатистически неподвижны относительно системы отсчета на его поверхности. Не исключено, что рассматриваемые пары сами по себе не обладают инертной массой (или же она «неизмеримо» мала). Среда вакуума переходит в волновое состояние исключительно от внешнего воздействия источника электромагнитных волн. Вследствие практической безынерционности передающих волновые колебания электрон-позитронных пар электромагнитные волны распространяются с предельно высокой скоростью относительно выбранной локальной системы отсчета. При столкновении с экранирующим препятствием волны ослабевают или прекращают распространение, оставляя на экране следы передававших их колебания корпускул. Корпускулы рассеиваются на экране в соответствии со свойствами волн, придавших им импульс. Корпускулы могут быть ансамблями электрон-позитронных пар и оставаться нейтральными, могут распадаться на пары электрона и позитрона, например, при прохождении космических лучей через атмосферу, образуя явление электрон-позитронных (электрон-позитронных фотонных) ливней. Процессы образования электрон-позитронных пар происходят при распаде γ-квантов в камере Вильсона (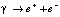
) [7–9], при генерации электрон-позитронной плазмы в сверхсильных лазерных полях [10]. Возможно, волновые свойства известных элементарных частиц в значительной мере зависят от электрон-позитронной среды их распространения.
Ниже детализируется предположение об электрон-позитронной среде вакуума (кратко – среда, если это не вызывает недоразумений) и электрон-позитронной структуре силовых линий гравитации в окрестности центра Земли, а также вблизи от ее поверхности с целью применить предположение к экспериментам по измерению скорости света. Для дальнейшего необходимо скорректировать полученные ранее соотношения. Изменение сводится к тому, что действие гравитации распространяется не только на физические тела, но и непосредственно на элементы силовых линий и элементы окружающей их среды.
Сам факт действия поля гравитации тела на элементы силовых линий и окружающей электрон-позитронной среды является следствием концепции близкодействия. Действие источника гравитации от элемента к элементу, то есть его действие на элементы силовых линий и окружающей их электрон-позитронной среды пространства, использовалось как основа для вывода аналога (16) закона всемирного тяготения.
При этом предполагалось, что абсолютную величину элемента действия точечного тела единичной массы в составе M на точечное тело единичной массы в составе m, в случае если элемент действия находился на расстоянии r от первого тела, можно представить дифференциалом (5). Дифференциал выражал модуль элемента действия множества силовых линий и окружающей их среды в проекции на линию центров oo1. Физически передача действия происходила через промежуточные элементы силовых линий и окружающей их среды. Следовательно, действие в полном физическом и количественном выражении достигало ближайших к точке o1 элементов и уже от этих элементов прилагалось к телу в точке o1. Аналогично это действие прилагалось к предшествующим элементам, проектировавшимся на линию центров. Поэтому в условиях близкодействия нет препятствий рассматривать элемент действия точечного тела массой M в точке o на любой элемент силовых линий и окружающей их среды.
Чтобы определить искомое действие гравитационного поля Земли на данные элементы, потребуется дополнительно охарактеризовать силовые линии гравитации и физические особенности элементов. Силовые линии гравитационного поля Земли на сравнительно малом расстоянии R от ее центра, незначительно выходящие за пределы земной поверхности,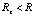 
, 
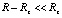, где Rz – средний радиус Земли, в первом приближении можно считать радиально направленными, а на локальном участке поверхности параллельными друг другу. Чтобы применить именно (5) (а не (18)) к рассматриваемым элементам силовых линий и окружающей их среды в качестве модуля элемента действия, необходимо формально предположить наличие массы рассматриваемых элементов. Существуют косвенные предпосылки допускать наличие массы элемента вакуума: электрон-позитронные пары состоят из компонентов, каждому из которых на основании экспериментов приписывается инертная масса. Однако масса элемента вакуума в макроскопическом измерении и масса физически минимального элемента вакуума – электрон-позитронной пары – принципиально различаются. Непосредственно ниже масса элемента силовых линий и окружающей их среды в макроскопическом измерении принимается как вспомогательное абстрактное понятие, используемое для количественной оценки действия поля гравитации Земли. Точнее, на время рассуждения первоначально абстрактно принимается предположение о наличии инертной массы рассматриваемого элемента, взятого в макроскопическом измерении.
Формально будут рассмотрены два случая. В первом – предполагается наличие инертной массы элемента силовых линий и окружающей их среды. Во втором – предполагается, что эта его масса равна нулю. В обоих случаях получатся эквивалентные выводы относительно скорости света противоположных направлений.
Пусть рассматривается первый случай. Каждая радиальная силовая линия гравитации Земли на рассматриваемом расстоянии от земной поверхности входит в пространство условно цилиндрической формы макроскопического диаметра, где состоит из элементов, расположенных вокруг продолжения от земной поверхности радиуса R как центральной высоты цилиндра. Диаметр цилиндрической поверхности с учетом масштаба источника гравитации можно считать достаточным, чтобы не оговаривать в дальнейшем возможность взятия внутри поверхности сколь угодно малого элемента в макроскопическом измерении. Суммы элементов действий силовых линий и окружающего их пространства можно рассматривать в проекции на центральную высоту цилиндра – на отмеченное продолжение радиуса R. Масса, входящая в элемент действия такой суммы, взятый в макроскопическом измерении, по-прежнему обозначается md.
Как отмечалось, силовые линии заполняют окружающее источник гравитации пространство в макроскопическом измерении непрерывно (они разделяются в пространстве микромира на межатомные расстояния в соответствии порождающим их ядрам атомов).
Гравитационное действие Земли, с оговорками относительно сферической формы и плотности, можно считать действием точечного тела в центре Земли массой Mz [11]. Пусть этот центр обозначен o и рассматривается действие из него на элемент (во избежание путаницы терминологии непосредственно ниже – на компонент) силовых линий и окружающей их среды пространства, расположенный на расстоянии R в точке o1. Линия центров oo1 располагается вдоль продолжения радиуса Земли Rz, которое, не умаляя общности, можно считать центральной осью силовой линии.
Вводится предположение, что элемент действия точечного тела единичной массы в составе Mz на компонент единичной массы m1 множества силовых линий и окружающей их среды пространства, расположенный на расстоянии r < R от центра Земли o в проекции на линию центров oo1, аналогично (5) по абсолютной величине может быть представлен дифференциалом
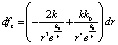, (21)
где
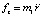. (22)
Полное действие на рассматриваемый компонент единичной массы в точке o1, расположенный на конце радиуса R, по абсолютной величине выразится интегралом
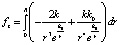. (23)
Согласно (7), (8) и (21)–(23) полное действие Земли на рассматриваемый элемент массой md примет вид
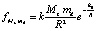, (24)
где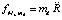 
. Здесь предполагается, что число цепочек вида (3) во множестве силовых линий пропорционально числу порождающих эти цепочки нуклонов центра гравитации (отсюда пропорция Mz). При выводе формулы, по аналогии с (7), (8) и (21), (22), сначала записывается соотношение для ускорения компонента единичной массы, 
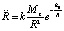, затем обе части равенства умножаются на md, в результате получится (24).
В (24) k может не совпадать с гравитационной постоянной γ. При взаимодействии двух тел, как в случае (16), силовые линии не радиальны и замкнуты. В случае (24) силовые линии радиальны и не замкнуты в точке o1 (на компонент массой md).
Тем не менее на время рассуждения (коэффициент k в преобразованиях сократится), принимается k = γ, – на том основании, что если бы на расстоянии R от центра Земли на месте рассматриваемого элемента находилось физическое тело массой md, то для него притяжение определялось бы из (24) при k = γ. Кроме того, соотношение с гравитационной постоянной для элементов силовых линий уже использовалось в неявной форме при выводе (16) для случая двух тел: действие (16) передавалось на элементы, расположенные на концах силовых линий гравитации. Если раскрыть выражение силы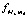 
, то (24) примет вид
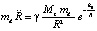, (25)
где на момент рассуждения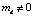 
. Из (25) центростремительное ускорение рассматриваемого элемента примет вид
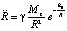. (26)
Соотношение (26) может быть получено без предположения о наличии ненулевой массы элемента силовых линий и окружающей их среды пространства. Для этого достаточно повторить рассуждения, выполненные относительно (18)–(20), применив их к рассматриваемому случаю. Содержание этих рассуждений и результат можно рассматривать как случай 2, в котором не предполагается наличие массы у элемента силовых линий и окружающей их среды пространства. Закономерность (18) для ускорения в этом случае должна априори предполагаться вместо закономерности (5). Отсутствие физического тела на расстоянии R вносит изменения в ранее принятую формулировку.
За элемент ускорения, вызванного действием точечного тела единичной массы в составе Mz на компонент множества силовых линий и окружающей их среды, расположенный на расстоянии R от центра Земли, принимается ускорение, вызванное полностью переданным действием на компонент на расстоянии R от элемента действия в проекции на линию центров, расположенного на расстоянии r от центра Земли (r < R). Элемент ускорения обозначается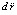 
и по абсолютной величине может быть представлен дифференциалом (18), где k = γ.
Из этой модификации априорного предположения (18) следует вывод соотношения (26). Соотношения (25), (26) показывают, что в любом из двух рассмотренных случаев, независимо от предположения относительно наличия массы, элемент множества силовых линий и окружающей их среды пространства в гравитационном поле Земли будет испытывать центростремительное ускорение (26). Поскольку R было выбрано произвольно (при отмеченных ограничениях), это утверждение относится к любому элементу множества силовых линий и окружающей их среды пространства. Ясно, что вместе с элементом в макроскопическом измерении ускорение испытывают все элементы множества электрон-позитронных пар, физически составляющих данный элемент. Согласно (26) ускорение элементов множества силовых линий и окружающей их среды пространства гравитационного поля Земли совпадает с ускорением свободного падения физических тел над земной поверхностью. На малом расстоянии от поверхности в стандартном измерении оно численно равно g = 9,80665 м/с2. Действие на элементы силовых линий и среды пространства в гравитационном поле таково, что вся среда вакуумного пространства в пределах радиуса длины R испытывает действие гравитационного притяжения Земли, оцениваемое, в зависимости от предположения, из (25) или (26). На малом удалении от поверхности вакуумная среда притягивается к центру Земли подобно физическим предметам на земной поверхности.
Независимо от принадлежности элемента силовым линиям или окружающему их пространству ниже как синонимы будут использоваться термины «элемент среды», «элемент вакуума», «элемент электрон-позитронной среды», «элемент среды вакуумного пространства». Термин «среда» будет синонимом термину «электрон-позитронная среда», при этом понятие «среда» и его синоним абстрагируются от понятия любой другой материальной среды пространства и от ее взаимодействия с электрон-позитронной средой.
Вследствие орбитального движения Земли вся окружающая электрон-позитронная среда, измеренная на расстоянии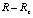 
от поверхности Земли, 
, 
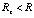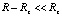, сопровождает движение це нтра Земли. Среда движется вдоль орбиты со скоростью центра, поскольку радиальные силовые линии образованы именно этим центром. Непрерывно пронизывая среду, своим взаимодействием с ней они определяют движение вместе с собой всей среды распространения света. Если луч света выпустить на земной поверхности по направлению орбитального движения Земли и в обратном направлении, то скорость движения луча в обоих направлениях будет одинаковой в силу того, что среда распространения света локально неподвижна относительно центра Земли. Это согласуется с эффектом постоянства скорости света в орбитальном и противоположном направлении и гипотетически объясняет эффект. В эксперименте Майкельсона [12] скорость света в двух направлениях – орбитальном и обратном – измерялась с помощью интерферометра на неподвижной платформе. Конструктивно интерферометр Майкельсона был выполнен так, что луч от источника раздваивался, часть его шла параллельно движению центра Земли, а часть – ортогонально. После отражения от зеркал лучи встречались в одной точке и создавали интерференционную картину. По результатам численной обработки интерференционной картины скорость света в обоих направлениях оказывалась одинаковой. Скорость вращения Земли вокруг оси в этом эксперименте не учитывалась.
Чтобы учесть суточное вращение Земли, необходимо принять во внимание, что во вращательном движении участвуют все элементы не только земной поверхности, но и всего заключенного в Земле объема материи. Это означает, что притяжение к центру Земли вдоль радиальных силовых линий гравитации будет происходить со смещением вслед за вращательным движением радиальных отрезков, на которых движущиеся вместе с ними нуклоны атомов порождают радиальные силовые линии. Точнее, действие Земли в любой точке окружающей среды является центростремительным, – в силу близкодействия оно направлено вдоль радиальных силовых линий гравитации, которые вращаются вместе со всей материей Земли и земной поверхности. В результате непрерывно заполняющие пространство радиальные силовые линии гравитации Земли и вся взаимодействующая с ними электрон-позитронная среда вблизи земной поверхности, в отмеченных границах расстояния R до центра Земли,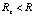 
, 
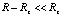, не только сопровождают орбитальное движение центра Земли, но и участвуют в суточном обращении Земли, включая вращательное движении поверхности вокруг земной оси. На такое движение оказывают влияние все вращающиеся элементы материи Земли, поэтому с учетом близкодействия вдоль радиальных силовых линий угловая скорость вращения среды равна угловой скорости суточного вращения Земли вокруг оси. Движение среды вдоль касательной к поверхности происходит с линейной скоростью ее вращения: среда, как и объекты на поверхности, вращается с линейной скоростью поверхности. Следовательно, в каком бы направлении на поверхности Земли ни выпустить луч света, скорость его движения в прямом и обратном направлении будет одинакова: среда распространения света локально неподвижна относительно источника, зафиксированного на поверхности Земли. Это согласуется с результатом эксперимента Майкельсона – Морли, согласно которому свет распространяется с одной и той же скоростью относительно произвольно расположенного источника на поверхности Земли [13]. В этом эксперименте интерферометр повышенной чувствительности, позволявшей учитывать скорость суточного вращения Земли, устанавливался на вращающейся платформе (массивная плита платформы плавала в ртути). Эксперимент проводился с установкой платформы по всем горизонтальным направлениям, в различное время суток, в различное время года, в течение года. Эффект постоянства скорости света в прямом и обратном направлении сохранялся во всех вариантах направления луча света. Современные эксперименты подтверждают этот эффект с применением лазерных излучателей и сверхчувствительных приборов регистрации скорости света [14].
Таким образом, изложенное выше предположение об электрон-позитронной среде пространства, движущейся с Землей в орбитальном направлении и вращающейся вместе с земной поверхностью, согласуется с результатами экспериментов Майкельсона, Майкельсона – Морли и дает им гипотетическое объяснение.
Эффект Саньяка заключается в разности фаз двух встречно распространяющихся световых волн по контуру при его вращении вокруг оси. Величина эффекта пропорциональна угловой скорости вращения интерферометра, частоте излучения и площади, охватываемой путём распространения световых волн в интерферометре: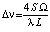 
[15, 16]. Ниже рассматривается кольцевой интерферометр Саньяка [16] («кольцевой интерферограф»), представляющий собой платформу с набором симметрично расположенных по кольцевому контуру зеркал. Платформа (стол) приводится во вращение на ртутной подушке. Два луча света выпускаются из одного источника (один луч, расщепленный призмой на две части) одновременно во встречных направлениях, обегают с помощью зеркал кольцевой контур и возвращаются в точку вблизи источника, где интерферируют на экране. Пока платформа неподвижна, интерференционные полосы от обоих лучей на экране одинаковы. Когда платформа приводится во вращение, интерференционные полосы расходятся, что соответствует разной скорости движения лучей света во встречных направлениях вращения. При этом количественно эффект всегда выражается приведенной выше пропорцией угловой скорости, частоте электромагнитного излучения и площади, охватываемой движением луча. Закономерность инвариантна относительно размеров применяемых интерферометров и их веса [16–18]. Поэтому для оценок предполагаемого влияния гравитации Земли можно принять единичную массу интерферометра, mi = 1 кг, единичный радиус кольцевой платформы, ri = 1 м = 10–3 км. Понадобится также масса Земли, Mz = 5,9736×1024 кг, радиус Земли, Rz = 6371 км. Абсолютная величина силы действия Земли на элемент электрон-позитронной среды массой md непосредственно вблизи земной поверхности определяется из (24), (25). Это действие Земли в любой точке окружающей среды должно быть строго центростремительным, поскольку в силу близкодействия оно направлено вдоль радиальных силовых линий гравитационного поля Земли, которые, как отмечалось, вращаются вместе с материей Земли и земной поверхностью. Абсолютная величина аналогичной силы действия на этот же элемент со стороны интерферометра – 
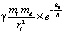. Отношение сравниваемых сил составит
,
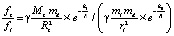или
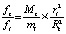. (27)
С учетом выбранных значений получится
.
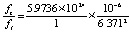Отсюда
,
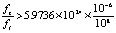или
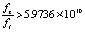(28)
Согласно (28) вектор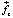 
рассматриваемого действия Земли на элемент среды по абсолютной величине более чем в 1010 больше вектора 
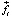аналогичного действия на тот же элемент со стороны интерферометра. Поэтому, как бы ни был направлен вектор действия интерферометра, при сложении с вектором действия Земли вектор суммы этих двух действий, 
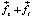, всегда будет направлен исключительно вдоль вектора действия Земли, то есть к центру Земли от любой точки «кольца» на платформе. При этом величина действия Земли на элемент среды при сложении двух данных векторов практически не изменится, 
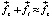. В результате вращение платформы интерферометра сохранит окрестную электрон-позитронную среду вакуума практически неподвижной относительно земной поверхности, каковой она являлась априори до начала вращения под действием силы 
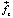притяжения к центру Земли. Среда будет отставать от вращательного движения платформы, два встречно распространяющихся вдоль ее кольцевого контура световых луча придут к равноудаленной точке их приема за разное время, что выразится в сдвиге интерференционных полос на экране в точке приема лучей. Тот факт, что величина эффекта пропорциональна угловой скорости вращения интерферометра, окажется «механическим» следствием локальной неподвижности среды относительно системы отсчета, зафиксированной в центре вращения платформы.
Если, исходя из (26), аналогично сопоставлять непосредственно ускорения, создаваемые гравитацией Земли и кольцевого интерферометра, то, соответственно, получится: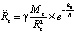 
, 
, 
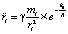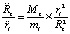. Иными словами, отношение абсолютных величин центростремительных ускорений равно отношению абсолютных величин сил из (27). Следовательно, 
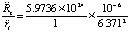и согласно (28) 
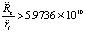. Отсюда вектор центростремительного ускорения 
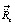элемента электрон-позитронной среды по абсолютной величине более чем в 1010 больше вектора ускорения 
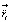того же элемента к центру масс интерферометра. При любом направлении вектора 
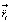их сумма 
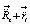останется направленной к центру Земли, при этом центростремительное ускорение элемента среды под действием Земли практически не изменится, 
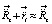. Суммарный вектор ускорения в силу близкодействия направлен строго вдоль радиальных силовых линий гравитационного поля Земли, которые, как отмечено выше, вращаются вместе с материей Земли и земной поверхностью. Поскольку речь идет об ускорениях, а не о силах, этот вывод получается без использования предположения о наличии массы у элемента среды вакуума. Утверждение о центростремительном ускорении элемента среды относится и непосредственно к физически наименьшим элементам – к электрон-позитронным парам, заключенным в элементе среды, взятом в макроскопическом измерении. Эти наименьшие элементы в среднестатистическом состоянии не будут увлечены вращательным движением платформы интерферометра: они будут локально неподвижны относительно системы отсчета, зафиксированной на земной поверхности, сохраняя ориентацию в соответствии ускорению к центру Земли. Таким образом, вывод о локальной неподвижности среды вакуума вдоль контура кольцевого интерферометра получается независимо от предположения о наличии массы у элемента вакуума.
Необходимо добавить, что в экспериментах, проводившихся с кольцевым интерферометром Саньяка, а также с самым крупным в истории его аналогом – кольцевым интерферографом Майкельсона – Гейла – Пирса, не было зафиксировано отставание от поверхности Земли среды распространения света в процессе суточного вращения [16]. Поиск велся на основании аналогии с отсутствием вращательного движения среды вслед за вращением платформы в опыте Саньяка. Поиск и не мог привести к положительному результату, поскольку среда распространения света не отстает от вращающейся поверхности Земли в границах малого удаления от земной поверхности, определяемых расстоянием R до центра Земли,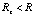 
, 
.
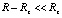Согласно изложенному гипотетическому объяснению электрон-позитронная среда вакуума не увлекается движением (в частности, вращательным) малого макроскопического тела по причине малого гравитационного действия на элементы среды, но сопровождает движение (в частности, вращательное вокруг оси) планет и небесных тел космического масштаба, гравитационное действие которых на элементы вакуумной среды влечет ее центростремительное притяжение.
Результаты исследования и их обсуждение
На основе предложенной гипотезы результаты экспериментов Майкельсона, Майкельсона – Морли и Саньяка могут объясняться наличием, а не отсутствием материальной среды передачи электромагнитных волн. Результаты этих экспериментов не отрицают наличие материальной среды вакуума, а отрицают лишь ее абсолютную неподвижность.
Изложенное выше предположение о связи вакуума с электромагнетизмом, гравитацией и веществом не входит в противоречие с результатами данных экспериментов.
В аспекте такой связи может казаться спорным предположение о дифференциале действия вида (5), (6). Этот формализм можно было бы отнести к элементу любой (не обязательно электрон-позитронной) абстрактной среды со свойством близкодействия и вывести из него аналог закона всемирного тяготения (16). Допустив, что электромагнитные волны распространяются в такой среде, можно было бы повторить объяснение опытов Майкельсона, Майкельсона – Морли и Саньяка. Однако в случае принятия такой абстракции не получалось бы вывести закон Кулона, как это сделано в [1]. В этом случае не было бы возможности описать прозрачный механизм взаимосвязи и действия электрического, магнитного и гравитационного полей; согласно предложенной гипотезе эти поля – разновидности взаимной ориентации элементов электрон-позитронной среды пространства, отсюда вытекает механизм соответственного близкодействия. В то же время принятый механизм позволяет объяснить изменение веса соленоидов при прохождении по ним переменного электрического тока, наблюдавшееся в опытах, описанных в [1]. В абстрактной среде не просматривается связь вакуума с веществом, не объясняется структура атома. Соотношения (5), (6) не вполне абстракция, они соответствуют закономерности взаимодействия электрических диполей, с которыми сходны электрон-позитронные пары. Предположение о биполярности вихревых элементов вакуума позволяет объяснить их происхождение в процессе зарождения вселенной на основе теории большого взрыва [1]. Ниже будет отмечено, что обсуждаемая модель вакуума, вещества, электромагнетизма и гравитации формализованно вытекает из предположения о связи инерции с гравитационным полем.
Как следствие изложенных предположений, электрон-позитронная среда вакуумного пространства сопровождает (вблизи поверхности) вращение небесных тел большой массы вокруг оси и движется с ними в орбитальном направлении. То же можно отнести к орбитальным и вращательным движениям звезд и галактик. Отсюда свет имеет постоянную скорость в сопровождающей среде относительно системы отсчета на поверхности небесного тела, аналогично относительно среды, сопровождающей движение звезд и звездных систем. Однако в системе отсчета, удаленной от сопровождающей среды и сопровождаемого центра гравитации, скорость света в локальной среде сложится со скоростью сопровождаемого небесного тела или системы тел по законам кинематики. Так, на поверхности Земли скорость света постоянна, а в системе отсчета в центре Солнца эта скорость будет складываться (с учетом направления) со скоростью движения Земли вокруг Солнца и со скоростью суточного вращения Земли. В системе отсчета в центре галактики эта скорость аналогично сложится со скоростью движения Солнца вокруг центра галактики и так далее.
Реальную информацию о скорости света в системах небесных тел несет свет, что создает сложность экспериментального наблюдения его скорости. Тем не менее большая часть кинематической информации, принимаемой от источников света (электромагнитных волн), является достоверной по следующим соображениям. Внутри отдельной галактики свет распространяется в электрон-позитронной среде, увлекаемой полем гравитации именно этой галактики. На удалении от звезд в этой же галактике среда распространения света представляется неподвижной относительно системы отсчета, помещенной на данном удалении в центр наблюдения, и относительно центра свет распространяется с постоянной скоростью в локально неподвижной среде. Если луч света проходит вблизи звездной или планетной системы, то в масштабе галактических расстояний – это малый отрезок на пути луча. В то же время скорость движения среды вблизи системы небесных тел составляет около 10% от скорости света. По всей длине пути луча в галактическом пространстве эти относительно малые изменения асимптотически не отразятся на средней скорости распространения луча в галактике. Здесь подразумевается допущение, что скорость света всегда постоянна относительно системы отсчета в локальной среде его распространения и что перемещение среды не придает механического импульса лучу света, поэтому физически не меняет его скорость и направление в данной локальной среде.
Межгалактическое пространство заполняет среда распространения света, в которой его скорость локально не меняется. Изменения скорости света вблизи галактик на пути распространения асимптотически редки. В данном случае, как и в предыдущем, можно пренебрегать изменением скорости света на пути его распространения в смысле асимптотической меры. Иными словами, допустимо утверждать, что скорость света в пространстве вселенной постоянна в асимптотическом смысле по длине пути и времени его распространения.
В локальной области пространства изменения скорости света можно учитывать и корректировать на основе информации о скорости и направлении взаимного смещения центров гравитации на пути луча.
Одно из следствий предположения об электрон-позитронной структуре вакуумного пространства связано с прохождением луча света непосредственно вблизи звезды. Внутренние процессы звезд (например, термоядерные реакции внутри Солнца и электромагнитные возмущения на его поверхности) возмущают окружающую электрон-позитронную среду, меняя структуру связи ее элементов. Элементы утрачивают свойство «безынерционности» при передаче электромагнитных колебаний, что может замедлить распространение света и повлиять на его направление, может возникнуть эффект запаздывания луча света вблизи поверхности звезды. Возмущенная среда вакуума может не только в различной мере ослаблять, замедлять прохождение света, изменять его направление, но может совсем не пропускать свет, как, например, в окружающем пространстве астрофизических черных дыр.
Основная гипотеза – следствие нестрогой дедукции, которая воспроизводится с целью по возможности снизить впечатление эклектичности не связанных между собой и не подтвержденных экспериментально частных предположений. Приведенные частные предположения – следствия трех основных предположений. Первое из них – физическая природа инерции движения связана с полем гравитации. Второе (оно – следствие первого, поэтому не самостоятельное предположение) состоит в том, что поле гравитации полярно: обладая притяжением, поле способно проявлять отталкивание. Если этого не предполагать, инерцию центробежного движения пришлось бы объяснять центростремительным действием гравитационного притяжения. Третье – электромагнитное и гравитационное поле взаимодействуют между собой по принципу близкодействия, по тому же принципу действует каждое из них в отдельности. Следующая схема рассуждений [2] приводит к гипотетической структуре нейтрона (нуклона). Пусть силовая линия поля понимается формально, по определению М. Фарадея, как линия движения пробного полюса (это отличается от неформального определения, использованного выше, где силовая линия понималась как линия движения пробного тела под действием элементов среды). У полярного поля гравитации два противоположных полюса. Сферическое однородное тело не может иметь радиальных силовых линий, иначе это означало бы, что два таких тела статистически отталкивают один и тот же пробный полюс, а значит, друг друга – в противоречии с законом всемирного тяготения (взаимное притяжение противоположного полюса влечет аналогичный вывод). По причине недопустимости аналогичных взаимодействий с полюсами силовые линии не могут составлять ненулевого угла с касательной плоскостью к сферической поверхности. Поэтому они расположены по сферам вокруг центра тяжести рассматриваемого тела. В силу симметрии статистических гравитационных взаимодействий силовые линии на такой сфере – окружности равного радиуса, равномерно заполняющие сферу без взаимных пересечений. Внутри сферы должна наблюдаться такая же картина, но она не может быть инвариантной по своей ориентации (по направлению движения полюса) без силовой линии противоположного полюса. Тогда силовые линии обоих полюсов расположены параллельно одна под другой, образуя сдвоенные окружности. При этом сдвоенные силовые линии двух полюсов не могут пересекаться ввиду наблюдаемого в статистическом состоянии только лишь притяжения тел и их элементов. По предположению поле гравитации взаимодействует с электромагнитным полем. Ничему не противоречит допущение, что рассматриваемые линии движения противоположных полюсов являются линиями движения противоположных электрических зарядов. Поскольку элементарные частицы обладают гравитацией, по силовым линиям их поля на сферической поверхности вокруг центра не могут двигаться дискретные электрон и позитрон. Поэтому с необходимостью каждый заряд – замкнутый вихрь и оба винтообразно (сжимаясь до минимальных размеров) вращаются в одном направлении (что исключает аннигиляцию). Остается доопределить свойства электрон-позитронной пары. Такими силовыми линиями должен обладать нейтрон как элементарная частица с полем гравитации. Отсюда следует его гипотетическая структура, описание которой предшествует иллюстрации на рис. 2. Чтобы принять близкодействие, неизбежно распространить предположение на (электрон-позитронную) структуру вакуума. В противном случае обрывается цепочка действия вещества на элемент вакуумной силовой линии.
Перенос соотношения (16) на случай взаимодействия с вакуумом в форме (24), k = γ, означает, что в условиях гипотезы близкодействия аналог (16) закона всемирного тяготения сохраняет силу как для взаимодействия физических тел друг с другом, так и для их взаимодействия с материей вакуума. Здесь необходима оговорка, что если предполагать массу элементов вакуума равной нулю, то эквивалентные формы закономерности принимают вид соотношения для ускорения (13) при значении k = γ.
Заключение
В предположении близкодействия на основе электрон-позитронной структуры вакуума и вещества, механизм которого реализует связь электромагнитного и гравитационного полей, показано, что результаты экспериментов Майкельсона, Майкельсона – Морли и Саньяка в совокупности могут объясняться наличием, а не отсутствием материальной среды передачи электромагнитных волн. Результаты этих экспериментов исключали не существование среды, а только лишь ее абсолютную неподвижность. В условиях близкодействия имеет место аналог закона всемирного тяготения для взаимодействия физических тел и их взаимодействия со средой вакуума. Элементы среды испытывают притяжение к физическим телам. Среда передачи электромагнитных волн, подчиняясь гравитационному притяжению, сопровождает орбитальное движение Земли и суточное вращение ее поверхности. В то же время малые тела на поверхности Земли не могут увлечь своим локальным движением среду распространения электромагнитных волн. Сумма вектора притяжения элемента среды телом малой массы и вектора притяжения Земли остается примерно равной вектору гравитационного притяжения Земли, поэтому оставляет элемент и всю локальную среду неизменно сопровождающими движение Земли и земной поверхности. Отсюда эффекты экспериментов Майкельсона, Майкельсона – Морли и Саньяка единообразно объясняются гравитационным взаимодействием Земли и тел на ее поверхности со средой распространения электромагнитных волн.