Процессы диффузии, проникновения и переноса вещества в различных средах могут сильно различаться по своей физической природе, но при этом быть описаны одними и теми же математическими моделями. Эти модели, как правило, носят сложный характер и могут включать в себя различные направления математики. Однако во многих случаях могут быть описаны дифференциальными уравнениями в частных производных. Часто такие уравнения сложны и не имеют аналитических решений, и приходится получать решения в частном случае или прибегать к численным методам. Сложность таких уравнений обусловлена процессом диффузии и массообмена в средах, свойства которой могут быть описаны различными моделями, и чем сложнее процесс и среда, тем сложнее уравнения.
Так, например, движение масс вещества в организме происходит за счет биохимических реакций. Важную роль играет движение масс вещества из внеклеточного пространства в клетки и, наоборот, из крови во внеклеточное пространство. Такое перемещение вещества связано с различием концентраций веществ в различных частях организма и движением этих веществ по концентрационному градиенту, что является процессом диффузии. Диффузия в растворе представляет скачки молекул из одного квазиравновесного состояния в другое, на расстоянии порядка 1Å. При этом происходит выравнивание концентраций по всей жидкости [1].
Цель исследования заключается в построении и получении дискретных решений общей системы уравнений, описывающих процесс диффузии и массообмена в различных средах.
Материалы и методы исследования
В работе используются методы численного моделирования систем дифференциальных уравнений, методы научных аналогий и методы теории подобия и размерности. В качестве основы материала исследований для описания процесса диффузии рассмотрим уравнение, связывающей пространственное и временное изменение концентрации (второй закон Фика) [2]:
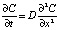 , (1)
, (1)
где С – концентрация вещества в жидкости; x – линейная координата перемещения вещества; D – коэффициент диффузии.
Следует отметить, что уравнение диффузии (1) справедливо при условии закона сохранения вещества в рассматриваемом объеме, при условии, что не происходит никаких химических реакций. Для учета реакций справедливо [2]:
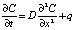 , (2)
, (2)
где q – скорость образования (связывания) молекул вещества.
Математическая модель возбуждения нейрона Лазарева имеет следующий вид [3]:
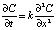 , (3)
, (3)
где k – коэффициент диффузии.
С учетом диффузии вещества уравнение (3) запишется в следующем виде:
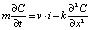 , (4)
, (4)
где m и v – некоторые постоянные; i – сила тока, притягивающая к перегородкам клеток ионы. Формально уравнения (2) и (4) одинаковы и описывают процесс одномерной диффузии вещества (солей, ионов и т.д.) в клетках.
На наш взгляд, принятые модели не вполне точно отражают реалии протекающего процесса в некоторых задачах. Например, если не существует перегородки x2 (рис. 1) и необходимо определить величину (глубину) х, на которую предельно проникают ионы. Необходимо также учитывать: скорость фильтрации; плотность солей; удельный объем солей за мембранной перегородкой, а также его изменение по времени t и расстоянию х.
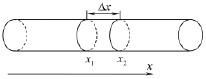
Рис. 1. Схема моделирования одномерной диффузии
Понятия, относящиеся к ионизации (скорость фильтрации, удельный объем солей, плотность), при формализации описываются понятиями скорости диффузии ионов, зарядом за перегородкой x1 и т.д.
Рассмотрим предлагаемые уравнения движения ионов посредством диффузии через мембрану x1 [2]:
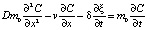 , (5)
, (5)
где D – коэффициент конвективной диффузии L3t-1; C – концентрация вещества (ионов) в жидкости, ML-3; x – удельный объем вещества (ионов, солей и т.п.) в среде в д. ед.; m0 – проницаемость (в некоторых случаях пористость); v – скорость фильтрации L3t-1; δ – плотность солей, ML-3. Здесь размерности величин даны в виде обозначений величин из теории подобия и размерности.
Левая часть уравнения (5) определяет ускорение изменения концентрации солей по величине перемещения х, с учетом диффузии D и проницаемости m0:
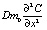 . (6)
. (6)
В правой части уравнения приведено выражение скорости изменения концентрации по времени с учетом проницаемости:
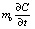 . (7)
. (7)
В уравнениях (1) и (3), по сути, приравнивают зависимости (6) и (7). На наш взгляд, необходимо учесть, что величина ускорения концентрации С по координате х уменьшается в зависимости от изменения скорости фильтрации v и скорости изменения концентрации по х: 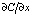 . Кроме того, очевидно, что на ускорение (6) влияет в сторону уменьшения плотность δ и изменение удельного объема ξ по времени. В связи с этим в уравнении (5) учтены в левой части второе и третье слагаемые.
. Кроме того, очевидно, что на ускорение (6) влияет в сторону уменьшения плотность δ и изменение удельного объема ξ по времени. В связи с этим в уравнении (5) учтены в левой части второе и третье слагаемые.
Воспользовавшись первой теоремой подобия, определим соответствие размерностей в правой и левой частях уравнения (5):
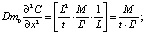 (8)
(8)
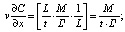 (9)
(9)
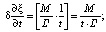 (10)
(10)
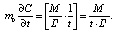 (11)
(11)
Все члены уравнения (5) имеют одинаковые размерности, что говорит о его применении для описания различных процессов в средах. При диффузии изменяется (или может изменяться) удельный объем ξ проникающего вещества. Его значение зависит от плотности обобщенного коэффициента ионоотдачи γ и предельной концентрации насыщения ионами Сm.
Скорость изменения ξ по времени описывается уравнением кинетики массопереноса вещества [4]:
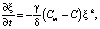 (12)
(12)
где k – коэффициент заполнения. Коэффициент k описывает физику ионизации: k = 0 – поверхностная (пленочная) ионизация; 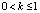 – объемная ионизация (дисперсная).
– объемная ионизация (дисперсная).
Таким образом, процесс диффузии и массообмена вещества можно описать системой уравнений:
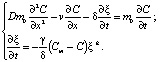 (13)
(13)
Для решения системы (13) необходимо задать начальные и граничные условия для функций C(x, t) и ξ(x, t). Для функции C(x, t) граничные условия могут принимать вид
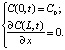
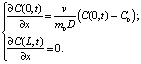 (14)
(14)
Особенностью первого условия (14) является мгновенное образование зоны постоянной концентрации Со на входной поверхности рассматриваемого участка (х = 0). Второе условие (14) выражает баланс диффузии ионов во входном сечении потока: расход ионов, поступающих в мембраны вследствие фильтрации Соv, равен расходу ионов на поверхности (x = 0), формирующемуся в результате диффузии, фильтрации и пористости. Использование этого условия даёт постепенную ионизацию входного сечения до концентрации Со. Второе условие (14) предпочтительнее первого условия (14). В обоих граничных условиях (14) в конечном участке х = L рассматриваемой области принимается, что скорость диффузии ионов в этом сечении постоянна и поэтому градиент концентрации равен нулю.
Также зададим начальные условия (t = 0) для функций ξ(x,t) и C(x,t):
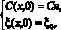 (15)
(15)
где Cн – концентрация в начальный момент времени вдоль оси x; ξ0 – величина удельного объема в начальный момент времени в области.
Таким образом, постановка задачи следующая: необходимо найти распределение концентрации C(x, t) и удельного объема ξ(x, t) вдоль оси х и во времени. В математической постановке эта задача сводится к решению системы (13) с условиями (14)-(15). Решение системы (13) в аналитическом виде представляет определенные математические трудности.
Для удобства решения введём безразмерную координату и время: 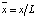 ,
, 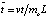 , тогда уравнения (13) и условия (14)–(15) можно записать для объемной ионизации (k = 1) в безразмерном виде:
, тогда уравнения (13) и условия (14)–(15) можно записать для объемной ионизации (k = 1) в безразмерном виде:
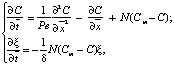 (16)
(16)
где 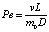 – критерий Пекле;
– критерий Пекле; 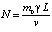 – критерий растворения. В новых обозначениях условия (14)-(15) примут вид
– критерий растворения. В новых обозначениях условия (14)-(15) примут вид
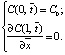
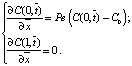 (17)
(17)
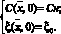 (18)
(18)
Таким образом, решение системы уравнений (13) с условиями (17)-(18) будет зависеть только от двух безразмерных критериев Pe и N, изменяя которые можно получить различные режимы процесса диффузии и изменения удельного объема проникающего вещества. Это позволяет получить решения 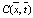 и
и 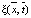 модельной задачи на отрезке
модельной задачи на отрезке 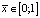 в безразмерном виде в зависимости от двух критериев Pe и N для различных процессов диффузии, фильтрации и кинетики переноса вещества в различных средах.
в безразмерном виде в зависимости от двух критериев Pe и N для различных процессов диффузии, фильтрации и кинетики переноса вещества в различных средах.
Для решения этой задачи был применен численный метод конечных разностей по неявной разностной схеме с использованием метода обратной прогонки. Как известно неявные схемы устойчивы и позволяют получить сходящиеся дискретные решения для любых соотношений шагов по аргументам 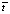 и
и 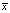 [5].
[5].
Решение уравнений (17)–(18) находится в области R = [0 ≤ 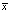 ≤ 1]×[0 ≤
≤ 1]×[0 ≤ 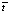 ≤ T]. В области R была введена равномерная прямоугольная сетка, образованная пересечением линий
≤ T]. В области R была введена равномерная прямоугольная сетка, образованная пересечением линий 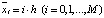 и
и 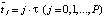 ; величины h, t являются шагами сетки по переменным
; величины h, t являются шагами сетки по переменным 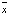 и
и 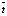 ;
; 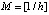 и
и 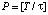 – целые части соответствующих дробей. Значения функций в узлах сетки обозначаются
– целые части соответствующих дробей. Значения функций в узлах сетки обозначаются 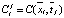 и
и 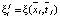 .
.
Конечноразностная схема для системы (16) имеет вид
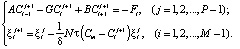 (19)
(19)
Граничные и начальные условия (17)–(18) имеют вид
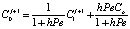 ,
,
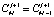 ,
, 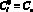 ;
; 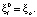 (20)
(20)
На каждом временном слое 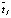 первое уравнение аппроксимированной системы (19) представляет собой систему линейных алгебраических уравнений для определения величин
первое уравнение аппроксимированной системы (19) представляет собой систему линейных алгебраических уравнений для определения величин 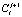 на следующем временном слое; правые части этих уравнений известны, поскольку содержат значения решения с предыдущего временного слоя. Решение системы линейных уравнений для определения
на следующем временном слое; правые части этих уравнений известны, поскольку содержат значения решения с предыдущего временного слоя. Решение системы линейных уравнений для определения 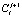 осуществляется методом обратной прогонки [5]. После определения
осуществляется методом обратной прогонки [5]. После определения 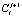 определяется
определяется 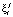 по второму уравнению системы (19). Таким образом, определяются значения концентрации диффузора
по второму уравнению системы (19). Таким образом, определяются значения концентрации диффузора 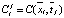 и удельного объема вещества
и удельного объема вещества 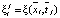 в дискретном виде для каждой точки по длине оси
в дискретном виде для каждой точки по длине оси 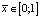 в течение времени
в течение времени 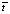 .
.
Результаты исследования и их обсуждение
На рис. 2 приведена зависимость распределения концентрации 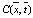 ионов во времени при различных значениях Pe и N в серединном сечении области
ионов во времени при различных значениях Pe и N в серединном сечении области 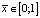 . Из распределения концентраций на рис. 2 видно, что при возрастании критерия Пекле и средних значениях критерия растворения концентрация ионов в фильтрующейся плазме сравнительно быстро достигает предельной концентрации насыщения Сm за счет увеличения скорости фильтрации и достаточно большого значения коэффициента ионоотдачи g. При малых значениях критерия Пекле и критерия растворения процесс растворения протекает значительно медленнее и концентрация убывает до величины С0 за счет того, что на входном сечении грунта происходит постепенное опреснение до величины С0 (вторые граничные условия (17)).
. Из распределения концентраций на рис. 2 видно, что при возрастании критерия Пекле и средних значениях критерия растворения концентрация ионов в фильтрующейся плазме сравнительно быстро достигает предельной концентрации насыщения Сm за счет увеличения скорости фильтрации и достаточно большого значения коэффициента ионоотдачи g. При малых значениях критерия Пекле и критерия растворения процесс растворения протекает значительно медленнее и концентрация убывает до величины С0 за счет того, что на входном сечении грунта происходит постепенное опреснение до величины С0 (вторые граничные условия (17)).
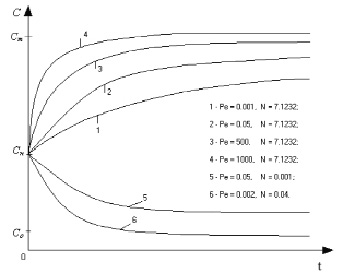
Рис. 2. Изменение концентрации диффузора ионов во времени
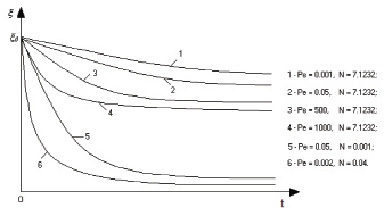
Рис. 3. Изменение удельного объема вещества среды во времени
На рис. 3 показана зависимость распределения удельного объёма 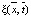 от времени также при различных значениях Pe и N в серединном сечении области
от времени также при различных значениях Pe и N в серединном сечении области 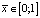 .
.
Из распределения удельного объема на рис. 3 видно, что при больших и малых числах Пекле, через определенное время, содержание удельного объема переносимого вещества в среде становится постоянным, что свидетельствует о насыщении ионами фильтрующейся среды до своего предельного значения Cm (или установлении фильтрата) и процесс изменения удельного объема x вещества из среды прекращается.
Заключение
Полученные решения для С и x системы универсальных дифференциальных уравнений в частных производных (16) с условиями (17)–(18) позволяют смоделировать процесс диффузии и массопереноса веществ в различных средах. За счет своей универсальности система по аналогии может описывать различные с физической точки зрения процессы диффузии и изменения удельного объема вещества в различных средах. Это позволяет использовать результаты решения при описании химических процессов, биохимических реакций в организмах, фильтраций жидкостей в средах, такие как грунты, почвы, атмосфера, дисперсные среды и т.п.

