Для определения кинематических характеристик плоского движения тела применяются как графические (метод планов), так и аналитические методы исследования. Планы скоростей и планы ускорений являются векторными решениями кинематических задач при применении теоремы о скоростях и теоремы об ускорениях плоской фигуры. Графические методы просты и наглядны, но у них невысокая точность, связанная с графическими построениями, и надо строить планы скоростей и ускорений для каждого положения механизма. В литературе, изучающей плоскопараллельное движение, отмечается, что с появлением ЭВМ техническое значение планов скоростей и ускорений утратило свой смысл. Но, с другой стороны, эти планы являются идеальным учебным материалом для изучения плоского движения. Высокоточные аналитические методы содержат сложные алгоритмы, понижающие мотивацию учебной деятельности. Эти обстоятельства определили цель данной работы.
Цель исследования – предложить аналитический метод определения основных кинематических характеристик плоского движения тела, удовлетворяющий следующим требованиям: обеспечивать высокую точность, содержать простой алгоритм, способствовать закреплению учебного материала по теме «Плоское движение твердого тела» и повышать мотивацию учебной деятельности.
Материалы и методы исследования
В учебной литературе по теоретической механике [1–3] для определения кинематических характеристик плоского движения твердого тела используются графические (метод планов и метод диаграмм) методы или вычисляются с помощью мгновенных центров скоростей и ускорений, или с помощью основной теоремы кинематики. В теории машин и механизмов (прикладная механика) эти методами также пользуются наряду с высокоточными аналитическими методами, в частности методом замкнутых векторных контуров, предложенным В.А. Зиновьевым [4]. В данной работе предлагается аналитический метод кинематического анализа плоских механизмов, звенья которого совершают плоскопараллельное движение с использованием метрических соотношений в векторных треугольниках планов скоростей и ускорений. Алгоритм этого метода заключается в том, что, используя планы положений механизма, планы скоростей и ускорений, а также свойства планов, определяются внутренние углы векторных треугольников в планах скоростей и ускорений точек звена и далее по теореме косинусов или синусов находят скорости и ускорения.
Изложение метода демонстрируется на примере кинематического анализа кривошипно-шатунного механизма, план положений которого изображен на рисунке, а, план скоростей – на рисунке, б, план ускорений – на рисунке, в.
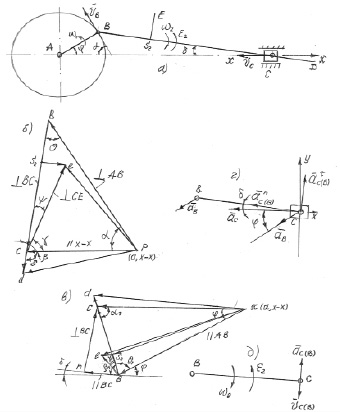
Метод планов: а) план положений; б) план скоростей; в) план ускорений; г) составляющие ускорения 
; д) направления ω2 и ε2 звена BC
Определение скоростей. Звено BC механизма совершает плоскопараллельное движение. Для построения плана скоростей решают систему векторных уравнений:
(1)
где 
– известная по величине и по направлению (перпендикулярно звену AB, в сторону вращения звена AB (подчеркнута двумя чертами)) скорость точки B, принимаемая за полюс;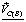 
– скорость точки C при вращении ее вокруг полюса B, известная только по направлению (подчеркнута одной чертой); 
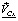– известная по направлению скорость точки C (направлена параллельно направляющей x-x).
Решая систему векторных уравнений (1), используя свойство подобия планов (плоские фигуры на плане положений и на плане скоростей геометрически подобны) в произвольном масштабе строится план скоростей для точек механизма, следуя разработанным отечественными учеными методикам [4, 5]. Точкам плана положений A, B, C, D, S2, E (рисунок, а) соответствуют точки плана скоростей p (a), b, c, d, s2, e (рисунок, б). Векторы, проведенные из полюса плана скоростей P, изображают абсолютные скорости, а векторы, не проходящие через полюс, изображают относительные скорости точек звена BCдля данного положения механизма (угла поворота звена AB – φ).
Из векторного треугольника pbc плана скоростей абсолютную скорость точки C вычисляем, применяя теорему синусов: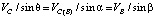 
=
= 
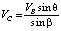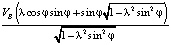(2)
VB – абсолютная скорость точки B, изображаемая отрезком pb и вычисляемая по формуле
VB = ωAB∙lAB = ω1∙lAB, (3)
здесь ω1 = ωAB – заданная постоянная угловая скорость звена AB; lAB – длина звена AB. VC(B) – относительная скорость точки C во вращательном движении вокруг точки B, изображаемая отрезком bc и вычисляемая по формуле
VC(B) = ωBC∙lBC = ω2∙lBC, (4)
где ω2 = ωBC – угловая скорость звена BC; lBC – длина звена BC. Из геометрических соображений и свойств планов скоростей вычисляем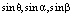 
:
;
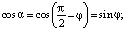
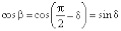
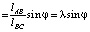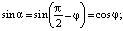
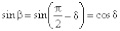
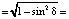
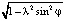; (5)
;
.
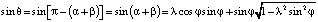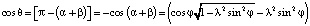Из векторного треугольника pbc плана скоростей также находим относительную скорость VC(B) точки C при вращении ее вокруг полюса B, применяя теорему синусов: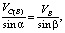 
откуда
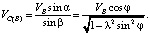(6)
По свойству подобия планов, составляя пропорции, находят положение точек S2, D, E звена BC на плане скоростей s2, d, e и величины их относительных скоростей. Для относительной скорости Vs2 точки S2 при вращении ее вокруг полюса B составим пропорцию:
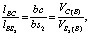
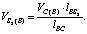(7)
Для относительной скорости VD(B) точки D при вращении ее вокруг полюса B составим пропорцию:
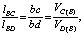
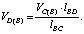(8)
Для относительной скорости VE(C) точки E при вращении ее вокруг полюса C составим пропорцию (точка C взята за полюс вместо точки B из удобства):
, 
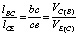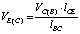. (9)
Применяя теорему косинусов в треугольнике pbs2 плана скоростей, вычислим скорость точки S2:
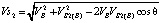. (10)
Применяя теорему косинусов в треугольнике pbd плана скоростей, вычислим скорость точки D:
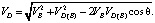(11)
Применяя теорему косинусов в треугольнике pce плана скоростей, вычислим скорость точки E:
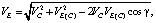
где
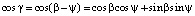
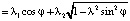. (12)
Здесь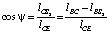 
, 
.
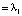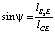
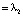Угловую скорость звена BC определим из формулы
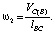(13)
Направление угловой скорости ω2 определится направлением вектора скорости VC(B), а для последующих значений φ также знаком VC(B) (изменение знака VC(B) на противоположный означает изменение первоначального направления ω2 на противоположное) (рисунок, д). Направление вектора скорости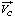 
при последующих значениях φ определится знаком VC (изменение знака VC на противоположный означает изменение первоначального направления вектора на противоположное) (рисунок, д).
Определение ускорений. Для построения плана ускорений (рисунок, в) решают систему векторных уравнений
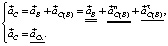(14)
где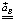 
– известное по величине и по направлению (направлено вдоль звена AB к центру вращения (подчеркнуто двумя чертами)) ускорение точки B, принимаемой за полюс (отрезок πв); 
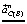– известное по величине и по направлению (направлено вдоль звена к точке B (подчеркнуто двумя чертами)) нормальное ускорение точки C (отрезок вn); 
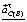– известное только по направлению (направлено перпендикулярно звену BC (подчеркнуто одной чертой)) тангенциальное ускорение точки C (отрезок nc); 
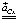– известное по направлению (направлено параллельно направляющей x-x) ускорение точки C (отрезок πс). Решая систему векторных уравнений (14), используя свойство подобия планов (плоские фигуры на планах положений и на планах ускорений геометрически подобны) в произвольном масштабе построен план ускорений, следуя методикам, разработанным отечественными учеными [4, 5]. Точкам плана положений A, B, C, D, E (рисунок, а) соответствуют точки плана ускорений a(π), b, c, s2, d, e (рисунок, в). Векторы, проведенные из полюса плана ускорений π, изображают абсолютные ускорения, а векторы, не проходящие через полюс, изображают относительные ускорения точек B, C, S2, D, E для данного положения механизма.
Из векторного треугольника πbc плана ускорений (рисунок, в) абсолютное ускорение точки C вычислим из пропорций (теорема синусов)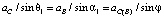 
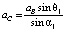, (15)
где aB – абсолютное ускорение точки В, равное нормальному ускорению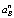 
(касательное ускорение точки 
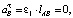так как угловая скорость звена AB ω1 = const) вычисляется по формуле
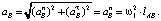(16)
Здесь ω1 = ωAB – заданная постоянная угловая скорость звена AB; lAB – длина звена AB. aC(B) – полное относительное ускорение точки C (отрезок вс) во вращательном движении вокруг точки B, вычисляемое по формуле
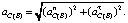(17)
Здесь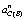 
– нормальное ускорение точки C во вращательном движении вокруг точки В, равное 
; 
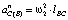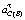– касательное ускорение точки C во вращательном движении ее вокруг точки B, равное 
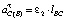(ω2 и ε2 угловая скорость и угловое ускорение звена ВС соответственно).
sin θ1 – синус ∠ πbc плана ускорений (рисунок, в);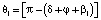 
.
Тогда
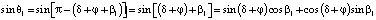. (18)
Здесь
, 
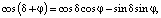
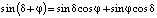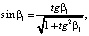
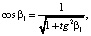
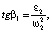
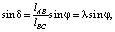
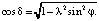
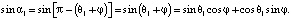(19)
Здесь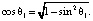 
Угловое ускорение ε2 звена BC вычисляется проецированием векторного уравнения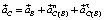 
на ось y-y, перпендикулярную известному направлению искомого ускорения 
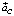(рисунок, г)
, 
,
, 
,
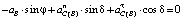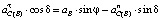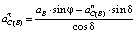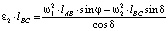откуда
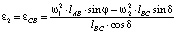. (20)
Направление ускорения звена ε2 определяется направлением вектора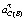 
(риcунок, г).
Относительные ускорения точек S2, D, E находятся из пропорций по свойству подобия планов.
Относительное ускорение точки S2 находится из пропорции
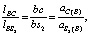
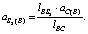(21)
Абсолютное ускорение точки S2 (отрезок πs2) находится по теореме косинусов
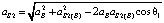. (22)
Относительное ускорение точки D находится из пропорции
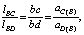
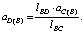(23)
Абсолютное ускорение точки D (отрезок πd) находится по теореме косинусов
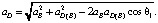(24)
Относительное ускорение точки Е находится из пропорции
, 
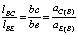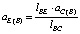, (25)
где lBE – расстояние между точками B и E звена BC, равное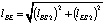 
.
Абсолютное ускорение точки Е (отрезок πе) находится по теореме косинусов из ∆ πbe (рисунок, в):
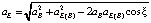. (26)
Здесь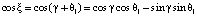 
, 
.
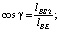
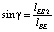Результаты исследования и их обсуждение
Результаты кинематического анализа кривошипно-ползунного механизма аналитическим методом с использованием метрических соотношений сведены в таблицу. Исходные данные: угловая скорость ω1 = 215 c–1; длины звеньев: lAB = 0,08 м; lBC = 0,3 м; lCD = lS2E = 0,05 м; координаты точек lBS2 = 0,09 м; угловая координата φ = 300.
Сравнительный анализ кинематических характеристик механизма
|
Результаты вычислений |
|||||||
|
Скорости |
VB 17,2 (17,2) |
VC 10,79 (10,4) |
VS2 14,09 (13,8) |
VD 11,4 (11,2) |
VE 11,04 (12,0) |
VC(B) 14,94 (15,0) |
ω2 49,8 (50,0) |
|
Ускорения |
aB 3698 (3698) |
aC 3880 (3700) |
aS2 3649 (3650) |
aD 4000 (3850) |
aE 3969 (3950) |
aC(B) 1917,79 (1900) |
ε2 5892 (5833,3) |
Примечание. Размерность линейной скорости м/с; размерность угловой скорости рад/с; размерность линейного ускорения м/с2; размерность углового ускорения рад/с2.
Сравнительный анализ кинематических характеристик механизма, полученных методом планов (скорости, ускорения в таблице даны в скобках) [4], показывает, что представленным в работе методом можно вычислять скорости и ускорения с любой заданной точностью.
Заключение
Предложен аналитический метод определения основных кинематических характеристик плоского движения твердого тела с использованием метрических соотношений в планах скоростей и ускорений на примере кинематического анализа кривошипно-ползунного механизма, облегчающий освоение студентами учебного материала по кинематике плоского движения твердых тел (теоретическая механика), повышающий мотивацию учебной деятельности. Простой алгоритм метода, высокая точность, наглядность позволит студентам решать не только учебные задачи, но и применять его в проектной деятельности.