Для оценки возможности композиционного построения структуры в инструментальной стали при упрочняющей термоциклической обработке (УТЦО) в настоящей работе впервые проведено физико-математическое и компьютерное моделирование процесса упрочняющей термоциклической обработки эвтектоидной стали У8 путем решения нелинейного уравнения Фоккера – Планка с использованием данных работ [1–3].
Физическая и математическая модели упрочняющей термоциклической обработки эвтектоидной стали
Для построения физической модели и математического описания процесса УТЦО условно принято нанокластерное образование [1] зернистого цементита Fe3C на предварительных перед закалкой стадиях неравновесного распада γ-твердого раствора в условиях незавершенных циклических твердофазных α↔γ превращений стали У8. Поэтому для упрощения моделирования термоциклической обработки (ТЦО) принято считать, что основной стадией формирования термоциклированной (ТЦ) структуры (рис. 1) является процесс распада аустенита с образованием глобулярного цементита Fe3C. На рис. 2 представлен фрагмент модельного зерна с нанокластерами Fe3C до и после ТЦО эвтектоидной стали. Как видно, момент времени to соответствует структуре фрагмента зерна с двумя исходными нанокластерами Fe3C до термообработки стали, а проведение ТЦО в период t0 + Δt приводит к зародышеобразованию трех новых нанокластеров Fe3C, а также росту всех (новых и исходных) нанокластеров Fe3C за счет диффузии атомов углерода из железоуглеродистой (Fe + C) матрицы в процессе распада γ-твердого раствора.
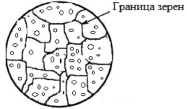
Рис. 1. Модельное представление структуры стали У8 после ТЦО
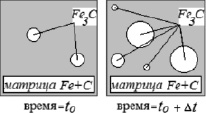
Рис. 2. Модельное представление фрагмента отдельного зерна стали У8 до и после ТЦО
При ТЦ нагреве стали происходит обратный процесс растворения в аустените нанокластеров Fe3C. Рост или растворение нанокластеров Fe3C приводит к изменению концентрации атомов углерода в Fe + C матрице зерна. Таким образом, в каждый момент времени t при ТЦО стали, предшествующей ее закалке на мартенсит, модельное зерно стали характеризуется следующими параметрами:
- концентрацией N(t) нанокластеров Fe3C;
- радиусом R(t) нанокластера Fe3C;
- концентрацией углерода C(t) в Fe + C матрице для данного зерна;
- функцией распределения F(R, t) нанокластеров по их радиусу в данный момент времени.
Зная функцию распределения F(R, t), можно рассчитать число нанокластеров Fe3C в зерне стали N(t), а также концентрацию атомов углерода C(t) в Fe + C матрице зерна стали после ТЦО на данный момент времени [2, 3] следующим образом:
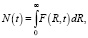 (1)
(1)
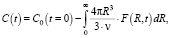 (2)
(2)
где ν – объём, приходящийся на один атом углерода С в фазе Fe3C; C(t = 0) – концентрация атомов углерода в Fe + C матрице (рис. 2) до проведения ТЦО эвтектоидной стали.
Изменение функции распределения нанокластеров со временем на диффузионной стадии роста и растворения фазы Fe3C было получено путем решения нелинейного уравнения Фоккера – Планка [2, 3], которое для изучаемой системы с нанокластерами фазы Fe3C (см. рис. 2) имеет следующий вид:
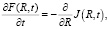 (3)
(3)
где J(R, t) представляется [2, 3] следующим образом:
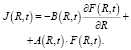 (4)
(4)
Функция A(R, t) определяется скоростью изменения эффективного радиуса нанокластера фазы Fe3C и имеет следующий вид:
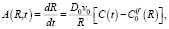 (5)
(5)
где D0 – коэффициент диффузии атомов углерода в кристаллической решетке железа;
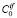 (R) – концентрация углерода на границе растущего нанокластера Fe3C, определялась по следующей формуле:
(R) – концентрация углерода на границе растущего нанокластера Fe3C, определялась по следующей формуле:
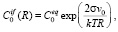 (6)
(6)
где 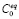 – равновесная растворимость углерода в кристалле железа при данной температуре; k – постоянная Больцмана; T – абсолютная температура; s – эффективная энергия единицы поверхности нанокластера Fe3C в Fe + C матрице; v0 – объем, приходящийся на один атом углерода в фазе Fe3C.
– равновесная растворимость углерода в кристалле железа при данной температуре; k – постоянная Больцмана; T – абсолютная температура; s – эффективная энергия единицы поверхности нанокластера Fe3C в Fe + C матрице; v0 – объем, приходящийся на один атом углерода в фазе Fe3C.
Задача построения функции распределения F(R, t) для численного моделирования процесса ТЦО была решена с помощью метода DAF (distributed approximating functional), основным свойством которого является возможность аналитического представления производных с помощью значений функции, заданных на дискретной сетке. В настоящей работе используется представление DAF через полиномы Эрмита.
Для решения уравнения Фоккера – Планка использовали физико-химические параметры (таблица), которые были определены с помощью квантово-химических расчетов [1, 4].
Расчетные параметры для решения уравнения Фоккера – Планка
|
Параметр |
Значение |
|
D – коэффициент диффузии атомов углерода в α-Fe |
D0 = 0,62 ∙ 10–2 cм2/c; ΔE = 0,86 эВ |
|
D – коэффициент диффузии атомов углерода в γ-Fe |
D0 = 0,49 cм2/c; ΔE = 1,6 эВ |
|
|
0,025 % С в α-Fe; 2,14 % С в γ-Fe |
|
s – эффективная энергия единицы поверхности нанокластера Fe3C в Fe+C матрице |
2,0–2,5 Дж/м2 |
|
v0 – объем, приходящийся на один атом углерода в новой фазе Fe3C |
3,86 ∙ 10–23 м3 |
|
|
|
а б
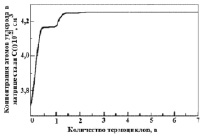
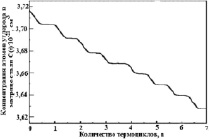
Рис. 3. Зависимость концентрации углерода С(t) в железоуглеродистой матрице в зависимости от числа циклов ТЦО эвтектоидной стали: а – N0 = 1 ∙ 1013 cм–3; Rsr = 8 ∙ 10–8 см; б – N0 = 5 ∙ 1012 cм–3; Rsr = 8 ∙ 10–5 см
Для решения уравнения Фоккера – Планка задаются следующие начальные условия:
1) функция распределения F(R, 0) нанокластеров Fe3C в Fe + C матрице до ТЦО стали У8;
2) концентрация N0 (R, t = 0) и радиус R0(t = 0) нанокластеров Fe3C до ТЦО стали У8;
3) концентрация атомов углерода C0(t = 0) в Fe + C матрице до ТЦО стали У8.
В конечном итоге с помощью уравнения Фоккера – Планка рассчитаны структурные параметры эвтектоидной стали во всех циклах проведения ТЦО.
Построение композиционной структуры термоциклированной стали в результате компьютерного моделирования
Компьютерное моделирование изучаемого процесса УТЦО осуществляли с помощью специальной программы, которая позволила в графическом виде представить результаты квантово-химических расчетов концентрации углерода и цементита в Fe + C матрице стали, а также радиуса нанокластеров цементита Fe3C в зависимости от числа циклов ТЦО, проходящей до проведения окончательной операции закалки стали. Анализ результатов при разных начальных структурных параметрах концентрации N0 и среднего радиуса R0 нанокластеров Fe3C показал, что с увеличением числа термоциклов ТЦО эвтектоидной стали формируются две группы зерен; в одних зернах Fe + C матрицы концентрация углерода С(t) возрастает (рис. 3, а), а в других зернах – уменьшается (рис. 3, б).
1. Первая группа включает в себя кристаллиты, в которых по мере увеличения числа термоциклов концентрация углерода возрастает, а концентрация нанокластеров цементитной фазы в стали уменьшается за счет растворения более крупных и образования более мелких включений цементита в Fe + C матрице [5]. Поэтому зерна первого типа все больше легируются углеродом в процессе прохождения ТЦО. А когда в Fe + C матрице большинство цементитных включений растворится, объемная доля зерен первого типа увеличится, а структура стали станет более однородной. Так как твердость стали зависит от содержания углерода в Fe + C матрице, можно предположить, что для зерен первой группы характерен рост их твердости, что после закалки делает сталь более твердой.
2. Вторая группа включает в себя кристаллиты, в которых в ходе термоциклирования концентрация углерода уменьшается, а концентрация нанокластеров цементитной фазы в стали не меняется, в то время как средний радиус цементитных включений увеличивается за счет роста старых и зародышеобразования новых включений цементита при диффузионном притоке углерода из Fe + C матрицы [5]. В результате ТЦО зерна второго типа становятся менее легированными углеродом с развитой зернограничной поверхностью и более пластичными. Поэтому можно предположить, что зерна второй группы обеспечат после закалки стали более высокие показатели пластичности и ударной вязкости.
В результате анализа отмечено, что при термоциклировании стали конкурируют два взаимно противоположных процесса: растворение цементитных фаз, с одной стороны; укрупнение и зародышеобразование включений цементита, – с другой, в результате чего после проведения ТЦО эвтектоидной стали формируется композиционная структура, состоящая из двух видов зерен с большой и малой концентрациями углерода. Модельный образец такой структуры представлен на рис. 4. Поскольку такая композиционная структура фиксируется при закалке и имеет мартенситную природу, показатели твердости и хрупкости у одних мартенситных зерен повышаются, а у других – снижаются.
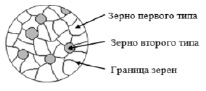
Рис. 4. Модель структуры стали, состоящей из двух типов зерен
С помощью теории эффективной среды и статистических методов расчета [6, 7] выведены формулы для определения эффективных параметров твердости HRC и ударной вязкости KC, которые учитывают значения HRC, KC в соответствии с относительным объемом каждого из двух типов зерен, имеющих разное содержание углерода. В результате получены расчетные значения эффективной твердости и ударной вязкости эвтектоидной стали У8 в зависимости от количества циклов УТЦО.
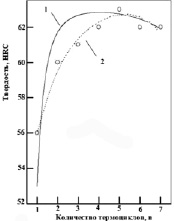
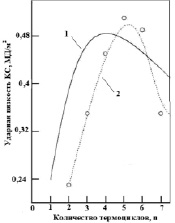
Графическая интерпретация расчетных и экспериментальных значений твердости и ударной вязкости эвтектоидной стали, подвергнутой УТЦО, представлена на рис. 5. Сравнительный анализ показал, что расчетная зависимость эффективной твердости и ударной вязкости стали У8 от числа циклов УТЦО носит экстремальный характер, такой же как в реальном процессе УТЦО (рис. 5), а разница расчетных и реальных значений твердости и ударной вязкости эвтектоидной стали У8 в оптимальной области варьируется от 5 до 30 %.
а б
Рис. 5. Расчетная и экспериментальная зависимости твердости (а) и ударной вязкости (б) стали У8 от числа циклов упрочняющей термоциклической обработки: 1 – расчетные данные, 2 – экспериментальные данные
Заключение
1. Проведенное квантово-химическое моделирование процесса УТЦО эвтектоидной стали научно доказало возможность формирования дискретной по углероду композиционной структуры, рационально сочетающей высокие показатели прочностных и пластичных свойств термоциклически обработанной стали.
2. С помощью математических методов расчета установлено скачкообразное повышение твердости и ударной вязкости стали У8 в зависимости от числа циклов УТЦО; такой же характер экстремальной зависимости получен в результате экспериментальных исследований влияния количества циклов процесса УТЦО на указанные механические свойства эвтектоидной стали.


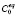 – равновесная растворимость углерода в кристалле железа при данной температуре
– равновесная растворимость углерода в кристалле железа при данной температуре