Среди многочисленных направлений в современной механике жидкости [1-3] присутствует успешно развивающееся актуальное направление, образованное исследованиями необычной, парадоксальной динамики гидромеханических систем [4]. Примером неординарного поведения гидромеханической системы может служить эффект, состоящий в том, что в поле силы тяжести твердое включение в жидкости, плотность которого отлична от плотности жидкости, при периодических по времени (колебательных, вибрационных) воздействиях, в среднем по времени (на фоне колебаний), не всплывает и не тонет – «левитирует», находится в состоянии «левитации» [5, 6]. В настоящей работе выявлены новые гидромеханические эффекты, в частности, обнаружен эффект «левитации» жидкости. Предметом изучения является новая задача о течении вязкой жидкости в поле силы тяжести при периодических по времени воздействиях. Жидкость контактирует с вертикальными твердыми стенками Ξ1, Ξ2. Границы стенок проницаемы для жидкости. Стенка Ξ1 совершает заданные периодические поступательные колебания вдоль осей X, Y, стенка Ξ2 – вдоль оси Y инерциальной прямоугольной системы координат X, Y, Z. Стенка Ξ1 ограничена плоскостью X = A, стенка Ξ2 – плоскостью X = L (L > A – постоянная). Жидкость заполняет область Ω (A < X < L , – ∞ < Y < ∞ , – ∞ < Z < ∞), втекает в область Ω и вытекает из нее через границы стенок.
Целью работы является определение движения жидкости.
Постановка и решение задачи
Пусть t – время; T – период колебаний стенок Ξ1 , Ξ2 ; τ = t / T; x = X / L; y = Y / L; z = Z / L; A = Ãsin2πτ (Ã > 0 – постоянная); a = A / L; ε = Ã / L; ex = {1, 0, 0}; ey = {0, 1, 0}; (dA / dt)ex + U1ey – скорость стенки (границы стенки) Ξ1; u1 = TU1 / L = ũ1sin(2πτ + α1) (ũ1 ≥ 0, α1 – параметры); U2ey – скорость стенки (границы стенки) Ξ2; u2 = TU2 / L = ũ2sin(2πτ + α2) (ũ2 ≥ 0, α2 – параметры); Qex + U1ey – скорость жидкости на границе стенки Ξ1; Qex + U2ey – скорость жидкости на границе стенки Ξ2; q = TQ / L = ε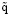 sin(2πτ + φ) (
sin(2πτ + φ) (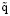 ≥ 0, φ – параметры); g = – g ey – ускорение свободного падения (g > 0 – постоянная); ϰ = gT2 / Ã; ρ, ν, V – соответственно плотность, кинематический коэффициент вязкости и скорость жидкости; v = TV / L = = vx(x,τ)ex + vy(x,τ)ey; P – давление в жидкости;
≥ 0, φ – параметры); g = – g ey – ускорение свободного падения (g > 0 – постоянная); ϰ = gT2 / Ã; ρ, ν, V – соответственно плотность, кинематический коэффициент вязкости и скорость жидкости; v = TV / L = = vx(x,τ)ex + vy(x,τ)ey; P – давление в жидкости;
P = T2P / (ρL2) = p(x,τ); Re = L2 / (vT) – число Рейнольдса.
Постановка задачи включает в себя уравнение Навье–Стокса, уравнение неразрывности и условия, которые должны выполняться на границах стенок Ξ1, Ξ2:
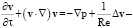 εϰey в Ω; (1)
εϰey в Ω; (1)
∇ · v = 0 в Ω; (2)
v = qex + u1ey при х = а; (3)
v = qex + u2ey при х = 1. (4)
Из (2) – (4) следует
vх = q для а ≤ х ≤ 1. (5)
Согласно (1), (3) – (5) имеем
Р = –2πε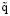 [cos(2πτ + φ)]x + p' в Ω; (6)
[cos(2πτ + φ)]x + p' в Ω; (6)
(p' – функция τ)
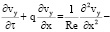 εϰ в Ω; (7)
εϰ в Ω; (7)
vy = u1 при х = а; (8)
vy = u2 при х = 1; (9)
Будем рассматривать задачу (7) – (9) при малых по сравнению с единицей значениях ε. Предположим, что
vy ~ v0 + εv1 при ε → 0. (10)
Используя (7) – (10), в εN – приближении (N = 0, 1) получим
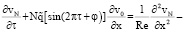 Nϰ в Ω; (11)
Nϰ в Ω; (11)
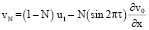 при х = 0; (12)
при х = 0; (12)
vN = (1 – N)u2 при х = 1, (13)
где Ω – область 0 < х < 1, – ∞ < y < ∞, – ∞ < z < ∞.
Пусть N = 0. Задача (11) – (13) имеет решение
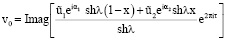 для 0 ≤ х ≤ 1. (14)
для 0 ≤ х ≤ 1. (14)
Здесь 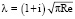 .
.
Пусть N = 1. Из (11) – (13) следует
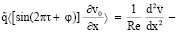 ϰ в Ω; (15)
ϰ в Ω; (15)
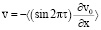 при х = 0; (16)
при х = 0; (16)
v = 0 при х = 1, (17)
где 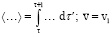 .
.
Задача (11) – (13) имеет решение
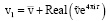 (18)
(18)
(ṽ– функция x).
Используя (14) – (17), найдем
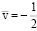 ϰ Re x(1–x) +
ϰ Re x(1–x) +
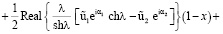
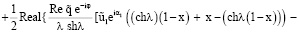
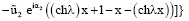 для 0 ≤ х ≤ 1 (19)
для 0 ≤ х ≤ 1 (19)
Формулами
vy = v0 + εv1 (20)
и (5), (6), (14), (18), (19) определяется приближенное решение задачи (1) – (4). Это решение свидетельствует о наличии ряда необычных, качественно различных (происходящих на фоне колебаний) стационарных течений жидкости. В частности, согласно (19) при 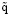 = 0,
= 0, 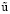 = 0;
= 0;
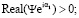 (21)
(21)
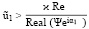
(Ψ = λ cth λ) для 0 ≤ х < 1 имеем
v > 0. (22)
Соотношение (22) означает, что жидкость ведет себя парадоксально – на фоне колебаний совершает стационарное движение в направлении, противоположном направлению ускорения свободного падения (то есть «снизу вверх»).
Отметим, что условие (21) для любого значения Re > 0 выполняется, например, при α1 = π / 4 – arg Ψ.
Обратимся к вопросу о среднем по времени течении жидкости при малых по сравнению с единицей значениях Re.
Пусть
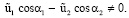 (23)
(23)
Используя (5), (14), (18) – (20), (23), получим
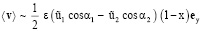
при Re → 0. (24)
Согласно (24) (на фоне колебаний) жидкость в области Ω
при 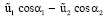 < 0 движется «сверху вниз»,
< 0 движется «сверху вниз»,
при 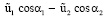 > 0 движется «снизу вверх».
> 0 движется «снизу вверх».
Пусть
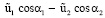 = 0. (25)
= 0. (25)
Используя (5), (14), (18) – (20), (25), получим
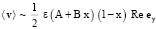
при Re → 0. (26)
Здесь
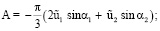
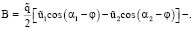 ϰ.
ϰ.
Согласно (26) (на фоне колебаний) имеет место следующее. При A ≤ 0, B < 0 и A < 0, B ≤ 0 жидкость в области Ω движется «сверху вниз»; при A ≥ 0, B > 0 и A > 0, B ≥ 0 жидкость в области Ω движется «снизу вверх»; при A > 0, B < 0 и –A / B < 1 жидкость, занимающая слой 0 < x < A / B, – ∞ < y < ∞ , – ∞ < z < ∞ движется «снизу вверх», а жидкость, занимающая слой –A / B < x < 1, – ∞ < y < ∞ , – ∞ < z < ∞ – «сверху вниз»; при A > 0, B < 0 и –A / B ≥ 1 жидкость в области Ω движется «снизу вверх»; при A < 0, B > 0 и –A / B < 1 жидкость, занимающая слой 0 < x < –A / B, – ∞ < y < ∞ , – ∞ < z < ∞, движется «сверху вниз», а жидкость, занимающая слой –A / B < x < 1, – ∞ < y < ∞ , – ∞ < z < ∞ – «снизу вверх»; при A < 0, B > 0 и –A / B ≥ 1 жидкость в области Ω движестся «сверху вниз»; при
A = 0, B = 0 (27)
жидкость в области Ω пребывает в состоянии «левитации» – находясь в поле силы тяжести, (на фоне колебаний) покоится. Отметим, что условия (25), (27) для любого значения ϰ > 0 выполняются, например, при
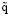 = 2π, φ = π / 2, ũ1 = ϰ / (3π),
= 2π, φ = π / 2, ũ1 = ϰ / (3π),
ũ2 = 2ϰ / (3π), α1 = π / 2, α2 = 3π / 2.
Заключение
Изучение представленной в настоящей работе новой задачи о течении вязкой жидкости в поле силы тяжести позволило выявить ряд новых эффектов необычного, парадоксального поведения жидкости. Данные эффекты имеют место при периодических по времени воздействиях, характеризующихся отсутствием выделенного направления в пространстве. Среди выявленных эффектов заслуживает быть отмеченным весьма «тонкий» эффект «левитации» жидкости, состоящий в том, что находящаяся в поле силы тяжести жидкость (без какой-либо опоры, на фоне колебаний) покоится, «левитирует».
Изложенное в настоящей работе может служить основой для проведения исследований, направленных на экспериментальное обнаружение выявленных теоретически новых гидромеханических эффектов, в частности, эффекта «левитации» жидкости.

