В настоящее время существует острая необходимость разработки эффективных и экологически безопасных технологий переработки растворов цветных металлов, целью которых является получение высокорентабельного продукта. Повышение рентабельности возможно за счет комплексности использования природных ресурсов, разработки замкнутых технологических схем, снижения экологических рисков в районах горно-обогатительных комбинатов. Для переработки сульфатных растворов цветных металлов используют сорбционные [1, 2] и экстракционные методы. Для сорбции применяют синтетические сильнокислотные [3, 4], слабокислотные [5], минеральные сорбенты [6] и биосорбенты [7, 8]. Многие исследователи изучали сорбцию ионов тяжелых металлов с использованием сульфо-катионитов.
Ранее нами показано [2, 9], что концентрирование растворов цветных металлов может быть проведено сорбционным методом с использованием промышленного катионита КУ-2-8. Сорбционная переработка сульфатных растворов бактериально-химического выщелачивания кобальт-медно-никелевых руд представляет собой актуальную задачу ввиду сложности состава подобных растворов.
В производственных условиях наиболее целесообразно проводить адсорбцию в сорбционных колоннах в динамических условиях. Следовательно, существует необходимость изучения сорбционного процесса в динамических условиях на сорбционных колоннах. При фильтрации через сорбционную колонну эффективность сорбции зависит от состава раствора, концентрации, наличия в растворе конкурирующих ионов, скорости фильтрации, высоты сорбционного слоя и др.
Целями настоящей работы являются определение сорбционных характеристик сульфо-катионита по отношению к меди, никелю, кобальту в динамическом режиме, установление зависимости сорбции катионов меди, никеля и кобальта из модельных растворов от высоты поглощающего слоя.
Для описания динамики сорбции на колоннах с неподвижным слоем сорбента используют различные модели. Рабочие характеристики колонны с неподвижным слоем удобно описывать с помощью кривых проскока [6, 7, 9], которые получаются путем построения графика зависимости отношения Ct/Co (где Ct и C0 – концентрация ионов металла на выходе и входе из колонны соответственно) от объема или времени вытекающего потока. Форма выходной кривой и время проскока являются важными характеристиками для определения работы колонны и ее динамического отклика.
Модель Томаса основана на предположении, что процесс следует ленгмюровской кинетике адсорбции-десорбции без осевой дисперсии [7, 10]. Основным преимуществом этой модели является простота применения в прогнозировании кривых проскока в различных условиях эксплуатации. Уравнение модели имеет следующий вид:
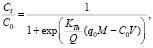(1)
где KTh – константа скорости Томаса, мл/мин∙мг; q0 – равновесная емкость адсорбента (мг/г); М – масса загрузки колонны, г; Q – объемная скорость потока (мл/мин); V – объем раствора, прошедшего через колонну, мл.
Уравнение (1) имеет вид линейной зависимости в координатах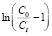 
от t, учитывая, что V = Q∙t:
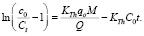(2)
Модель Адамса–Бохарта [7, 8] в основном используется для расчетов на начальном участке выходной кривой и описывается уравнением:
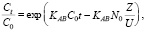(3)
где KAB – кинетический коэффициент Адамса–Бохарта, мл/мг∙мин; Z – высота слоя сорбента в колонке, см; No – объемная концентрация насыщения сорбента, мг/мл; U – линейная скорость, рассчитанная путем деления объемной скорости потока на площадь сечения колонки, см /мин.
Логарифмический вид уравнения (3):
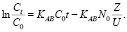(4)
Расчет параметров уравнения Адамса–Бохарта проводят путем построения зависимости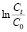 
от t методом линейной регрессии (4).
Зависимость времени службы от высоты слоя (BDST-модель) [10, 11] описывается модифицированной формой уравнения:
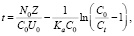(5)
где Ka – константа скорости в модели BDST (л/мг∙мин), остальные значения параметров такие же, как и раньше. Расчет параметров производят графоаналитическим способом по зависимости t от Z.
Материалы и методы исследования
В работе использовали катионит КУ-2-8, который представляет собой сополимер стирола и дивинилбензола. В качестве функциональных групп в смоле присутствуют сульфогруппы –SO3H. Смола КУ-2-8 имеет насыпную массу 0,75−0,90 т/м3. К достоинствам можно отнести высокую скорость обмена в связи с доступностью сульфогрупп, к недостаткам – низкую избирательность сорбции. Подготовка катионита КУ-2-8 проведена по известной стандартной методике, ранее использованной нами [2, 9]. Сорбционная колонка представляла собой стеклянную трубку диаметром 10 мм, высота слоя сорбента в зависимости от опыта составляла 10, 20 и 30 см, элюирование проводили методом нисходящего потока, объемную скорость потока поддерживали на уровне 1,0 мл/мин. Растворы, выходящие из колонки, подвергали химическому анализу. Определение содержания меди, никеля и кобальта выполняли атомно-абсорбционным методом с атомизацией в ацетилено-воздушном пламени, на приборе ААС-6300 Shimadzu (Япония) по стандартным методикам. Измерение рН проводили с использованием иономера «SevenCompact» фирмы «Mettler-Toledo Instrument (Shanghai) Co. Ltd» с универсальным электродом с точностью не ниже, чем ± 0,03 ед. рН.
В работе использовали модельные растворы, которые готовили, растворяя точные навески солей цветных металлов: CuSO4∙5H2O (ч.д.а.); NiSO4∙7H2O (х.ч.); CoSO4∙7H2O (ч.д.а.).
Результаты исследования и их обсуждение
По результатам экспериментальных исследований построены зависимости отношения текущей концентрации металлов (мг-экв/л) к начальной концентрации Сt/Co на выходе из колонки от времени (рис. 1). Расчет степени заполнения сорбента проводили, суммируя концентрации металлов в колонке в зависимости от времени (мг-экв/л).
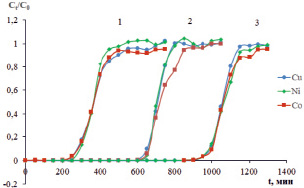
Рис. 1. График зависимости соотношения концентраций ионов металлов Сt/С0 от времени на выходе из колонок: 1 – высота слоя сорбента 10 см; 2 – 30 см; 3 – 30 см
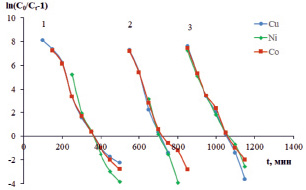
Рис. 2. Зависимость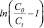 
от времени согласно модели Томаса (уравнение 2):
1 – высота слоя сорбента 10 см; 2 – 30 см; 3 – 30 см
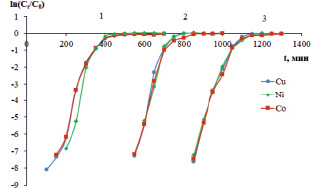
Рис. 3. Зависимость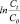 
от времени согласно модели Адамса-Бохарта (уравнение 4):
1 – высота слоя сорбента 10 см; 2 – 30 см; 3 – 30 см
Выходные кривые имеют S-образную форму. Практическое значение максимально достигнутой суммарной сорбционной емкости составило, мг-экв/г: 3,19, 3,15, 3,03 при высоте слоя сорбента 10, 20 и 30 см соответственно. При этом практическая максимальная сорбционная емкость по отдельным металлам составила, мг-экв/г: Cu2+ – 0,919 ± 0,036; Ni2+ – 1,019 ± 0,035; Co2+ – 1,184 ± 0,051. Проскок ионов металлов наступает при 14 %-ном насыщении колонки при высоте слоя сорбента 10 см, при увеличении высоты слоя сорбента до 20 см проскок наступает при 54 % насыщения. Максимальная степень насыщения до проскока 80 % наблюдается при высоте слоя сорбента, равной 30 см. Наиболее информативной характеристикой, описывающей работу сорбционной колонны, является безразмерная величина, связывающая диаметр сечения колонки D и высоту слоя сорбента Z, применительно к растворам, содержащим мель, никель и кобальт в равных концентрациях на уровне 500 мг/л. Отношение D к Z должно быть не менее 25, тогда проскок наступает при 80 % насыщения.
Для расчета константы скорости сорбции Томаса (KTh, мл/ мг мин) и максимальной равновесной емкости сорбента (q0, мг/г) построены графики (рис. 2) в координатах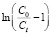 
от t согласно уравнению (2). Расчет вели по регрессионным уравнениям. Высокие значения коэффициентов корреляции R2 свидетельствуют о применимости модели Томсона для описания сорбции ионов металлов из модельных растворов с использованием сульфокатионита КУ-2-8.
Коэффициенты корреляции R2 находятся на уровне 0,961–0,996 (таблица). Теоретически рассчитанная суммарная сорбционная емкость составляет 3,42, 3,39 и 3,04 мг-экв/г при высоте слоя сорбента 10, 20 и 30 см соответственно. Превышение суммарной теоретической сорбционной емкости находится на уровне 6,72 % и 7,08 % при высоте слоя сорбента 10 и 20 см, а при высоте слоя 30 см изменений не выявлено. Значения константы скорости Томаса (мл/мг мин) при высоте слоя 10 см для меди и никеля составляют 0,074–0,075, для кобальта – 0,60, при высоте слоя 20 см для меди и никеля KTh повышаются до уровня 0,100–0,098, а для кобальта – до 0,067. При высоте слоя 30 см наблюдается снижение константы Томаса для меди и никеля и повышение для кобальта.
Константы модели Томаса KTh, модели Адамса–Бохарта KAB, емкость сорбента q0, концентрация насыщения сорбента N0 и коэффициенты корреляции
|
Компонент |
Z, см |
KTh, мл/мг мин∙ |
q0, мг/г |
R2 |
KAB, мл/мг мин |
N0, мг/мл |
R2 |
|
Cu |
10 |
0,074 |
29,9 |
0,967 |
0,082 |
12,6 |
0,966 |
|
20 |
0,100 |
32,1 |
0,988 |
0,099 |
14,2 |
0,981 |
|
|
30 |
0,086 |
29,3 |
0,996 |
0,081 |
13,1 |
0,982 |
|
|
Ni |
10 |
0,075 |
35,0 |
0,961 |
0,089 |
15,2 |
0,968 |
|
20 |
0,098 |
32,8 |
0,989 |
0,097 |
14,6 |
0,999 |
|
|
30 |
0,075 |
30,0 |
0,993 |
0,075 |
13,3 |
0,987 |
|
|
Co |
10 |
0,060 |
37,7 |
0,972 |
0,068 |
16,0 |
0,970 |
|
20 |
0,067 |
37,2 |
0,965 |
0,085 |
15,9 |
0,995 |
|
|
30 |
0,070 |
32,3 |
0,988 |
0,071 |
14,3 |
0,986 |
Для расчетов коэффициентов уравнения модели Адамса–Бохарта (3) построены графики зависимости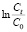 
от времени (рис. 3). Расчеты вели методом линейной регрессии. Значения кинетического коэффициента КАВ (мл/мг∙мин) и концентрации насыщения N0 и коэффициенты корреляции представлены в таблице.
Из графика зависимости (рис. 3) следует, что модель Адамса-Бохарта может быть применена на участке графика, когда степень насыщения сорбента не превышает 90 % насыщения. Значения кинетического коэффициента КАВ (мл/мг∙мин) варьируют от 0,068 до 0,099 в зависимости от высоты слоя сорбента и природы катиона. Высокие коэффициенты корреляции позволяют сделать вывод о применимости модели Адамса–Бохарта для описания процессов сорбции меди, никеля и кобальта из смешанных растворов.
Для расчета времени службы сорбционной колонны от высоты слоя сорбента использовали модель BDST, уравнение 5. Зависимость t от Z представлена на рис. 4. Построение графика (рис. 4) и расчеты вели по суммарной концентрации ионов металлов, равной 45,13 мг-экв/л.
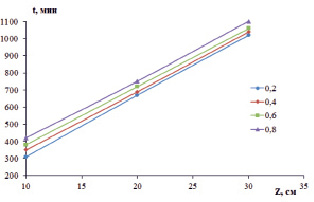
Рис. 4. Зависимость времени службы сорбционной колонны от высоты поглощающего слоя: 0,2, 0,4, 0,6, 0,8 отношение Ct/C0
Модель BDST – это упрощенная модель, которая не учитывает массоперенос внутри частицы и перенос во внешней пленке. Необходимыми допущениями явились условия эксперимента: постоянство суммарной концентрации ионов металлов на входе в колонну и скорости потока на протяжении всего времени работы. Константа скорости Ka, равная 2,7∙10–3 л/мг-экв∙мин, характеризует скорость переноса ионов металлов из жидкой фазы в твердую. Значения константы скорости Ka уменьшаются по мере насыщения сорбционного слоя. Рассчитанные параметры позволяют произвести масштабирование колонны без дополнительного эксперимента.
Заключение
В результате экспериментального исследования сорбции ионов меди, никеля и кобальта из модельных растворов при совместном присутствии в концентрациях на уровне 450 ± 50 мг/л по каждому катиону установлено, что проскок катионов наступает при 14 %-ном насыщении сорбента при высоте слоя 10 см, при 54 %-ном насыщении при высоте слоя 20 см и 80 %-ном насыщении при высоте слоя 30 см.
Модель Томаса применима для описания процесса сорбции вплоть до полного насыщения сорбционной колонны. Рассчитаны значения коэффициента Томаса для меди, никеля и кобальта при сорбции из модельных растворов, содержащих одновременно катионы меди, никеля и кобальта. Модель Адамса–Бохарта применима для описания процесса сорбции до степени заполнения колонны на 90 %.
Скорости переноса ионов металлов из жидкой фазы в твердую, согласно модели BDST, при низких степенях насыщения характеризуются константой скорости Ka, равной 2,7∙10–3 л/мг-экв∙мин. Значения константы скорости Ka уменьшаются по мере насыщения сорбционного слоя. Полученные данные позволяют прогнозировать форму выходных кривых и время службы колонны и могут быть использованы при масштабировании сорбционной установки.
Автор выражает благодарность за проведение аналитических исследований сотрудникам НИГТЦ ДВО РАН: ведущему инженеру Т.И. Ратчиной и инженеру А.А. Ряховской.