Численный анализ показал, что при больших величинах зазоров трапециевидные волны 1:п в системах с распределенными ударными элементами, вызываемые вибрацией прямой стенки, разрушаются и могут устанавливаться режимы весьма сложной структуры.
Такое явление вызывается рассогласованием между моментами ударов и геометрическими параметрами конфигураций трапециевидной волны и может быть объяснено возникновением стохастического ускорения.
Положим для простоты R = 1, и пусть возбуждение h(t) = -Δ - ε - ε cos ωt, νk >> εω. Это преобразование описывает поведение любой точки из отрезка удара. Введем переменную τk = {1/2 π-1 ω tk}, где скобки обозначают дробную часть числа: 0 < τ < 1. После вычислений имеем из
Светлые точки - опыты П.П. Осипова. Сплошная линия - расчет по формуле (10). Пунктирная линия - результаты расчета в предположении, что лопасть не вращается, а перемещается поступательно причем во втором равенстве отброшен малый член, времени нахождения струны в «зоне вибрации». Внося первое уравнение во второе, с точностью до членов ε2ω2 получаем
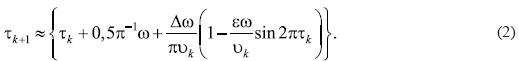
Преобразование (2) определяет отображение интервала (0,1)
на себя. Оно будет растяги
вающим, если 
. Получаем условие
возникновения стохастической неустойчивости:
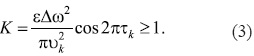
Неравенство (3) не имеет
места, если Δ = 0 (трапециевидные волны изохронны: ω = 2π) или если 
(удары всех точек
приходятся на координаты и = -Δ - ε). При K < 1 преобразование (12)
определяет периодические или почти периодические режимы. При K > 1 ввиду случайности последовательности {tk} дотрезки удара (и вместе с
ними трапециевидные профили стоячих волн) распадаются. Исследование
характеристик профилей распавшихся волн представляет собой самостоятельную
проблему. Однако, как указывалось, в ряде случаев стоячие волны способны
сохранить «изломанные профили».
Работа выполнена при поддержке РФФИ (проект № 10-08-00500-а).