Голографическую запись можно охарактеризовать особенной, присущей только ей передачей информации в области пространственного спектра частот. На общий объем информации, переносимой голографической системой, влияют множество факторов, характерных именно для голографического процесса. К этим факторам можно в первую очередь отнести факторы, влияющие на полосу пропускания пространственных частот, среди которых можно выделить апертуры входной и выходной частей оптической системы, т.е. апертуры линз, используемых для образования картин интерференции, ширины записывающего и опорного пучков, апертуры линз, используемых для восстановления голограммы, размер голограммы или ее отдельной страницы. В цифровом случае это еще и размеры фотоматрицы, которая записывает оцифрованную голограмму. К факторам, влияющим на итоговый размер записанной информации, относятся также и размеры самого объекта, характеристики полученной голограммы в области пространственных частот и, что очень важно учитывать, характеристики записывающей фотоматрицы [1–3].
Как уже упоминалось выше, при рассмотрении голографической системы необходимо учитывать не только параметры системы в области пространственных частот, но и параметры апертур всех элементов оптической системы, которые задаются в этом случае с помощью координат сигнала, представленного в оптическом виде. Можно это также сделать, задав параметры в виде значений отношения сигнал/шум или степени квантования оптического сигнала [4–6]. Важность рассмотрения апертурной характеристики при учете потерь информации в пространственной области заключается в том, что запись голограммы – это процесс преобразования координатной информации в информацию в области пространственных частот. То есть и в этом случае мы можем оценивать именно потери в области пространственных частот [7–9].
Целью данной работы является общий анализ голографических систем с точки зрения их возможностей по передаче информации в области пространственных частот, влияние на эту возможность пропускаемых системой пространственных частот и координатно-апертурных характеристик оптической системы.
Возможные потери информации при передаче ее в голографической системе
Возможные потери информации в обобщенной голографической системе, если рассматривать ее как устройство для передачи пространственной информации, можно объяснить с помощью нескольких причин. Среди них самыми важными являются факторы, определяющие изменение значения величины параметра сигнал/шум при переходе от одного участка голографической системы к другому или при переходе от одного диапазона частот к другому. Чаще всего значительные потери в системе происходят при переходе от низких частот к более высоким частотам. Общие потери проявляются не только в виде уменьшения полного объема передаваемой информации, но и в виде уменьшения ее плотности.
Учет всех упомянутых факторов позволяет провести анализ возможных потерь информации в голографической системе.
Если разбить голографическую систему, в соответствии с типом обработки изображения, на ступени, то способность пропускать данные для отдельного этапа можно задать следующим соотношением
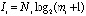 .
.
где i – номер этапа, Ni – количество пикселей числового разбиения изображения, проходящее сквозь апертуру i-го этапа, mi – число уровней квантования для каждого пикселя при условии, что количество пикселей попадающих в апертуру i-го этапа равно Ni [10–12]. При условии, что число пикселей, приходящихся на единицу площади апертуры i-го этапа, равно 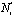 , а апертурная площадь равна si, можем записать
, а апертурная площадь равна si, можем записать
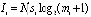 . (1)
. (1)
Особенностью любого этапа является то, что рост частоты пространственного спектра приводит к уменьшению значения mi. Если принять во внимание тот факт, что голографическая запись на тонкослойных записывающих средах приводит к различным информационным плотностям в двух взаимно перпендикулярных направлениях, то возникает необходимость рассматривать по отдельности частотные спектры вдоль этих направлений. В этом случае mi (vx, vy) можно представить в виде
mi (vx, vy) = m0i δi (vx), δi (vy). (2)
где δi (vx) = m(vx) / m0 – нормированная величина, получающаяся в результате разделения переменных. Значение этой величины может быть меньше или равно единице (здесь m0 – наибольшее значение m при некоторых усредненных значениях частот). Рассмотрим оптимизацию этапа голографической системы. Следствием оптимизации этапа голографической системы является необходимость деления апертуры этого этапа на такое число пикселей N, при котором частота v пространственного спектра задает величину m(v) так, чтобы общее количество информации, пропускаемое системой, стало максимально большим [13–15].
В апертуру голографической системы вдоль одной координаты укладывается 2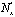 пикселей, что соответствует теореме отсчетов Шеннона. Отсюда следует, что общий объем информации, пропускаемый i-м этапом системы, можно представить в виде
пикселей, что соответствует теореме отсчетов Шеннона. Отсюда следует, что общий объем информации, пропускаемый i-м этапом системы, можно представить в виде
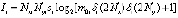 (3)
(3)
или
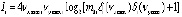 . (4)
. (4)
В качестве критерия при выборе общего числа пикселей в голографической системе надо брать не только число пикселей для самой малой апертуры на одном из этапов системы, но и тот факт, что от этапа к этапу в системе происходит уменьшение значения величины сигнал/шум. Важным моментом является отладка голографической системы с целью согласованной работы всех этапов системы, так как в противном случае происходят дополнительные потери информации при прохождении системы. Функциональная зависимость величины сигнал/шум при росте частот по отношению к нулевым и слабым частотам на i-м этапе голографической системы задается величинами δi (vxi) и δi (vyi). Величина сигнал/шум изменяется также и в поперечных оптической оси системы направлениях – вдоль осей xi и yi. Это происходит в случае неравномерности сигнала в поперечном направлении. Зависимость значения сигнал/шум от координат в этом случае определяется величинами βi (xi) и βi (yi). Значения δi (vxi), δi (vyi) и βi (xi), βi (yi) определяются в основном величинами сигнал/шум Ψ. Запишем значение сигнал/шум для заключительного этапа голографической системы в следующем виде (5):
Ψвых  . (5)
. (5)
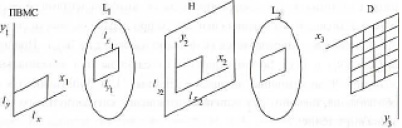
Рис. 1. Основные этапы голографической системы, влияющие на возможные потери информации: ПВМС – пространственно-временной модулятор света; L1, L2 – линзы, образующие этап преобразования объектной волны при записи и восстановлении голограммы; Н – голограмма; D – фотоматрица
В соотношении (5) подразумевается, что функция Ψ(vx, vy, x, y) разделяется на независимые переменные. Значения ξ характеризуют изменчивость величины сигнал/шум при переходе от одного этапа голографической системы к другому.
Анализ показывает, что на каждом этапе голографической системы частота, при которой пропуск информации максимален, больше, чем для всей голографической системы. То есть общий объем информации, пропускаемый системой, меньше, чем объем, пропускаемый на каждом этапе.
Проанализируем, как происходит изменение величины сигнал/шум на этапах голографической системы, которая показана на рис. 1. Это, в свою очередь, позволит сделать оценку плотности и общего объема пропускаемой голографической системой информации.
В голографической системе присутствуют три этапа, влияние которых максимально на ее информационную пропускающую способность. На первом этапе происходит считывание информации, вводимой в голографическую систему. На втором этапе происходит преобразование вводимой информации – в нашем случае это преобразование Фурье, которое осуществляется либо отдельной линзой, либо системой линз, входящих в голографическую систему. На данном этапе происходит формирование картины интерференции за счет сложения преобразованного объектного луча и опорной волны. Третий этап – это процесс записи полученной интерференционной картины на цифровой или аналоговый носитель.
На первом этапе информация может вводиться либо дискретным образом, в виде отдельных пикселей, либо аналоговым образом, в виде непрерывного изображения. И в первом, и во втором случаях возникают ограничения при вводе, обусловленные апертурой системы.
Дискретный ввод информации в голографическую систему изначально ограничивает общий объем информации самим процессом дискретизации – определяется шаг дискретизации, задаются максимальные значения пространственных частот vx max и vy max, фиксируются размеры страниц для вводимой информации lx и ly. Все это приводит к тому, что информация в процессе ввода передается полностью или частично теряется. Если потерь нет, то
I = 4 lx max ly max vx max vy max . (6)
В аналоговом случае дискретизация, тем не менее, осуществляется на выходе голографической системы в момент считывания фотоматрицей, причем на шаг дискретизации сильно влияют возможные потери информации на этапах голографической системы. Объем информации, пропускаемый голографической системой, в этом случае равен (7):
I = 4 lx max ly max vx max vy max log2[m0δ(vx max)δ(vy max) + 1].
На этапе ввода информации в голографическую систему формируется транспарант, зависящий от пространственной частоты. Эта зависимость задается переменными δ(1/α1vx) и δ(1/α1vy). Зависимость от координат можно приближенно задать с помощью величин β1(α1x) = β1(α1y) = 1. Эти зависимости определены до границ страниц ввода информации x = lx max и y = ly max. Вне этих границ β(x) = β(y) = 0. Для данного этапа ξ1 < 1.
Второй этап – это обычно либо отдельная линза, либо система линз, осуществляющих преобразование Фурье. Потери на этом этапе малы, поэтому ξ2 ≈ 1. Тем не менее и на этом этапе присутствуют небольшие потери информации, обусловленные такими факторами, как слабое пропускание линзами высоких пространственных частот, ограниченность апертур линз. Этих ограничений при построении голографических систем необходимо избегать. С этой целью надо использовать линзы с низкими значениями аберрации и большой апертурой, что позволит избежать потерь высокочастотных составляющих изображений. Принимая во внимание тот факт, что в целом голографическая система осуществляет преобразование Фурье, можно записать соотношения, связывающие координаты x2 и y2 на выходе голографической системы с амплитудными и фазовыми характеристиками пространственного спектра входного изображения, в виде vx2 = x2 / λf и vy2 = y2 / λf. Аналогичные соотношения можно записать для обратной последовательности vx1 = x1 / λf и vy1 = y1 / λf.
Третий этап – это этап записи прошедшей сквозь голографическую систему пространственной информации на цифровой или аналоговый носитель. Данный процесс сопровождается дополнительными шумами, величина которых задается неравенством ξ3 < 1. Кроме того, в этом случае также присутствуют потери в частотной области, величина которых определяется значениями δ(vxout) и δ(vyout). Принимая сказанное во внимание, необходимо на выходе голографической системы учесть изменение как координатных характеристик, т.е. β3 = (x / λf) и β3 = (y / λf), так и ограничения в области пространственных частот δ3(vx), δ3(vy) по плоскости голограммы (vx3 = lx2 / λf, vy3 = ly2 / λf). Необходимая информация считывается в пределах области, ограниченной координатами –lx / 2 и +lx / 2 вдоль оси х и yH – ly / 2 и yH + ly / 2 вдоль оси у. На рис. 2 представлены зависимости для β и δ вдоль оси y.
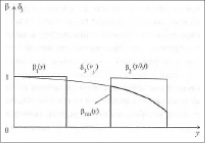
Рис. 2. Изменение величин β1, β2, δ3 и βres вдоль оси у выходной плоскости
На рис. 2 показано, что основной вклад в скорость изменения отношения сигнал/шум в выходной плоскости дает значение δ3, определяющее частотную характеристику голограммы.
Заключение
Голографическая система рассмотрена как многоступенчатая структура, каждая ступень которой дает определенный вклад в потери информации, проходящей сквозь систему.
На первой ступени информация может вводиться либо дискретным образом, в виде отдельных пикселей, либо аналоговым образом, в виде непрерывного изображения. И в первом, и во втором случаях возникают ограничения при вводе, обусловленные апертурой системы. Показано, что для оптимизации системы, направленной на уменьшение потерь информации, максимальные пространственные частоты vx max, vy max, а с ними и размер апертуры (страницы) должны быть оценены заранее.
Вторая ступень – это система линз, осуществляющих преобразование Фурье. Здесь также присутствуют потери информации, обусловленные такими факторами, как слабое пропускание линзами высоких пространственных частот и ограниченность апертур линз. Для преодоления этих ограничений необходимо использовать линзы с низкими значениями аберрации и большой апертурой, что позволит избежать потерь высокочастотных составляющих изображений.
Третий этап – это этап записи, прошедшей сквозь голографическую систему пространственной информации на носитель. Данный процесс сопровождается дополнительными шумами, которые необходимо учитывать, подстраивая выход голографической системы на возможные изменения информации в координатной и частотной областях.

