1. Актуальность темы
В настоящее время существует множество открытых проблем в области космологии. В частности, до сих пор неизвестно, существуют ли пространства размерности большей трёх [1] или многомерные пространства являются лишь математической абстракцией. В связи с этим логично поставить вопрос о существовании явлений, связанных с многомерной моделью пространства. Если наличие четвёртого пространственного измерения действительно имеет место, это может быть обнаружено по некоторым физическим явлениям, которые до настоящего времени считаются необъяснимыми космологическими аномалиями. Большое количество необъяснимых аномалий связано с происхождением, строением, движением галактик, а также их расположением в пространстве.
1.1. Проблема происхождения спиральной структуры галактик
Неясно происхождение спиральных рукавов. Неизвестно на сегодняшний день, почему большинство галактик имеют спиральную структуру, но при этом существуют также галактики, не обладающие спиральной структурой. Существует семь различных гипотез, отчасти противоречащих друг другу. «Столь большое число развиваемых в наши дни гипотез происхождения спиральных ветвей галактик показывает, что поставленная проблема не разрешена» [2]. Более того, в 2018 г. астрономов удивил новый открытый факт: на краю галактик оказались старые звезды, в противоположность существующим представлениям и ожидаемым результатам [3]. Кроме того, в [3] также отмечается недавно обнаруженный факт: все галактики, независимо от формы и размера, вращаются с периодом 1 миллиард земных лет. Такая синхронность также не имеет объяснения.
1.2. Проблема аномального характера вращения галактик, противоречащего законам Кеплера
В 1959 г. [4] для галактики М33, а позже, в 1970-х гг., и для других галактик был открыт факт аномального характера вращения. Ротационная кривая не убывает обратно пропорционально росту квадратного корня от расстояния, как следовало бы из законов Кеплера, а является почти плоской, то есть линейные скорости звёзд во всём диске галактики практически не отличаются друг от друга. Эта закономерность представлена на рис. 1, где по горизонтали указано расстояние от центра галактики (килопарсек), по вертикали скорость вращения (км/с).
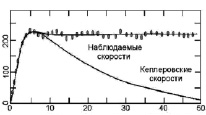
Рис. 1. Ротационная кривая: ожидаемая и фактическая
Более того, по другим данным, ротационная кривая даже несколько возрастает по мере удаления от ядра галактики, что видно из известной диаграммы, представляющей скорости вращения звёзд в галактике М33:
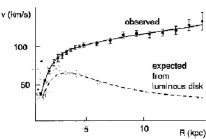
Рис. 2. Скорости вращения звёзд в галактике М33
Таким образом, скорость движения звёзд в галактике не убывает с ростом расстояния до центра галактики, в отличие от подобного изменения скоростей в планетарных системах. В связи с этим необъяснимы следующие явления:
А) Происхождение аномально большого вращательного момента и поддержание такого вращательного момента в течение длительного времени.
Б) Сохранение галактики как единой структуры. При таких линейных скоростях во внешней части диска, звёзды не были бы удержаны гравитацией и должны были уже давно покинуть галактику, рассеявшись в межгалактическое пространство, если бы не существовала либо некая скрытая масса, либо неизвестные дополнительные центростремительные силы.
В) Сохранение спиральной структуры галактик. Время обращения звёзд вокруг ядра галактики составляет сотни миллионов лет, а время существования галактик – миллиарды лет. Спиральные структуры за это время должны были полностью быть размыты и исчезнуть за счёт различий в угловых скоростях вращения звёзд вокруг ядра галактики.
1.3. Внегалактические парадоксы
1.3.1. Проблема анизотропного расположения галактик в видимой части Вселенной.
Но ситуация не исчерпывается перечисленными выше проблемами. Существуют необъяснимые явления, связанные с глобальным расположением галактик в видимой части Вселенной. По данным анализа распределения галактик, проведённого группой профессора Майкла Лонго в рамках проекта Galaxy Zoo [5, 6], в северной небесной полусфере более распространены левозакрученные спирали, а в южной – правозакрученные. Этот факт является одной из загадок космологии, ведь очевидно, что Земля, в силу ничтожности своей массы по сравнению с галактиками, не может оказывать влияние на то или иное распределение галактик. Тем более, не может оказывать такого влияния расположение земного экватора, связанное с вращением Земли вокруг своей оси. Поэтому логично предположить существование каких-либо ранее не известных космических сил, обусловливающих такое расположение галактик.
1.3.2. Синхронность периода вращения галактик.
В [3] также отмечается недавно обнаруженный факт: все галактики, независимо от формы и размера, вращаются с периодом примерно 1 миллиард земных лет. Такая синхронность также не имеет объяснения и свидетельствует о некотором вселенском надгалактическом процессе.
1.3.3. Аномалия вращения спутников больших галактик.
Многие десятилетия астрономы, руководствуясь компьютерными моделями, считали, что карликовые галактики во Вселенной «разбросаны» случайным образом. В 2013 г. было обнаружено, что небольшие галактики движутся по упорядоченным дискообразным орбитам. Это наблюдение сделано международной командой астрономов, в том числе профессором Герейнтом Льюисом (Geraint Lewis) из Школы Физики Сиднея, и опубликовано в журнале Nature. Карликовые галактики, окружающие Туманность Андромеды, вращаются вокруг нее в одной плоскости, диаметр которой более миллиона световых лет. Большая часть пар спутниковых галактик имеет противоположно направленные скорости, в том случае, если они расположены на противоположных сторонах гигантских галактик. Это противоречит всем стандартным космологическим моделям. По мнению ученых, ответ нужно искать в некоем в настоящий момент неизвестном физическом процессе, очевидно, что вследствие большого расстояния (1 миллион световых лет), гравитационных сил недостаточно для того, чтобы данный процесс был возможным.
2. Постановка задачи
В процессе поиска решения как галактических парадоксов, так и аномалий движения в Солнечной системе, усилия большинства исследователей сосредоточены на поисках «тёмной материи». Однако асимметричное расположение галактик во Вселенной не объяснить даже с помощью тёмной материи. Возможно, следует искать вовсе не неучтённую массу, а неизвестные дополнительные силы, которые преобладают (даже по сравнению с гравитационными) для объектов масштаба галактик, аналогично тому, как гравитационные силы преобладают по сравнению с электромагнитными в планетарных системах.
В случае если трёхмерное пространство является четырёхмерной гиперсферой и эта гиперсфера вращается, неизбежно будет иметь место проявление этого вращения в виде действия сил Кориолиса на каждую движущуюся в пространстве частицу. Таким образом, если наличие четвёртого пространственного измерения действительно имеет место, это может быть обнаружено по некоторым физическим явлениям, которые до настоящего времени считаются необъяснимыми космологическими аномалиями. Шарообразность Земли и её вращение можно обнаружить по некоторым наблюдаемым физическим явлениям, аналогичная ситуация возможна и для Вселенной, пространственная размерность которой на один больше, чем изначально наблюдаемая.
Факт вращения четырёхмерной гиперсферы, если таковой имеет место, может быть обнаружен изнутри гиперсферы по наличию дополнительных сил Кориолиса. В данной работе будет установлен вид тензора сил Кориолиса для случая, когда трёхмерное многообразие является фрагментом вращающейся четырёхмерной гиперсферы; построена абстрактная математическая модель, объясняющая, какие физические эффекты происходят вследствие воздействия сил Кориолиса на движущиеся космические тела.
3. Сила Кориолиса в пространстве произвольной размерности
Формула вычисления ускорения Кориолиса в трёхмерном пространстве имеет вид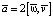 
, где 
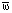– вектор, направленный вдоль оси вращения и пропорциональный угловой скорости вращения, 
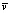– вектор скорости относительного движения. Ускорение Кориолиса вычисляется по отношению к неподвижной системе отсчёта, поэтому сила Кориолиса направлена в противоположную сторону и при учёте массы M тела равна 
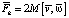. В то же время напрямую перенести формулу сил Кориолиса, известную из трёхмерной физики, на четырёхмерный случай не представляется возможным по следующим причинам:
1) в четырёхмерном пространстве отсутствует такое понятие, как бинарное векторное произведение пары векторов. Существуют обобщения векторного умножения на многомерные случаи, но они не являются бинарными операциями;
2) для вращающейся в R4 плоскости перпендикулярное направление не единственно, а существует перпендикулярная ей плоскость, поэтому нет однозначно определённого вектора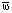 
, который присутствует в формулах сил Кориолиса для трёхмерного пространства. Поэтому необходимо изначально как-то иначе описать силы Кориолиса, используя только понятие плоскости вращения, но не используя аппарат векторного умножения. В данной работе это будет сделано с помощью линейных операторов.
Сначала получим метод вычисления силы Кориолиса без использования векторного умножения в трёхмерном пространстве. Пусть в плоскости 0xy происходит вращение с угловой скоростью ω. Тогда движение точек в пространстве задаётся с помощью линейного оператора:
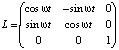
Пусть точка движется в пространстве таким образом, что траектория является гладкой кривой, тогда уравнения её движения на некотором бесконечно-малом промежутке времени можно представить как уравнения прямолинейного равномерного движения:
,
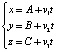где (А, В, С) начальная точка, (v1, v2, v3) вектор скорости относительного движения. Композиция этих движений вычисляется с помощью произведения матриц:
= 
.
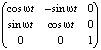
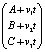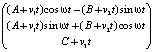Первая производная этой векторной функции:
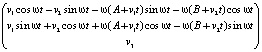
Вторая производная этой векторной функции:
=
+ 
=
+ 
=
.
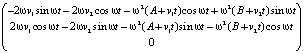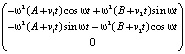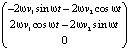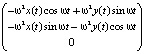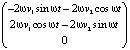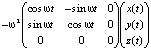
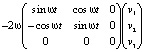Таким образом, вторая производная состоит из двух слагаемых. Одно из них есть вектор, направленный в плоскости вращения к центру (центростремительное ускорение, его модуль равен ω2R). Второе – вектор, который лежит в плоскости вращения и перпендикулярен как оси вращения, так и проекции скорости на плоскость вращения. Это и есть ускорение Кориолиса. Так, например, в момент времени t = 0 вторая производная равна
= 
.
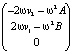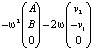Сила Кориолиса направлена противоположно ускорению Кориолиса и равна
.
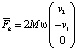Покажем, что это тот же вектор, который получился бы при применении формулы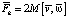 
, если ось вращения направлена по оси 0z и угловая скорость равна ω:
= 
= 
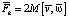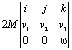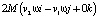, где i, j, k – оси координат. Это в итоге можно записать в виде вектора-столбца 
.
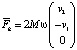Таким образом, мы без операции векторного произведения установили тот факт, что сила Кориолиса зависит от величины проекции вектора скорости на плоскость вращения. Если движение точки происходит вдоль оси вращающейся системы и проекция на плоскость вращения нулевая, то сила Кориолиса равна нулю. Теперь получаем возможность исследовать аналог сил Кориолиса в том числе и в многомерных пространствах, а не только в трёхмерном.
4. Вычисление сил Кориолиса в точках четырёхмерной гиперсферы
Кратко опишем структуру вращения в четырёхмерном пространстве. Существуют четыре взаимно перпендикулярных оси, обозначим их 0x, 0y, 0z, 0w. Вращение происходит в двух взаимно перпендикулярных плоскостях, пересекающихся лишь в начале координат. Пусть вращение в плоскости Oxy происходит с угловой скоростью ω1, а в перпендикулярной ей плоскости Ozw – с угловой скоростью ω2. Тогда вращение всего четырёхмерного пространства может быть задано линейным оператором:
.
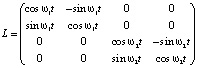При этом не существует как таковое понятие оси вращения, привычное в трёхмерном пространстве. В отличие от трёхмерного пространства, перпендикуляр к плоскости вращения не является единственным. Для плоскости Oxy все векторы плоскости Ozw являются перпендикулярами к Oxy. Можно говорить лишь о плоскости того или иного вращения, то есть существуют 2 инвариантных подпространства.
Методом, аналогичным рассмотренному в § 3, получим следующее. Сила Кориолиса зависит от величины проекции вектора скорости на каждую из двух плоскостей вращения и равна
.
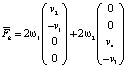Проекция вектора скорости точки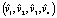 
на каждую из двух плоскостей вращения определяет проекцию силы Кориолиса на эту же плоскость. Сумма данных проекций есть сила Кориолиса при движении в четырёхмерном пространстве. Отметим, что в трёхмерном пространстве такая плоскость всего одна.
Однако далее необходимо учесть, что вектор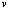 
не может быть произвольным, так как нам нужно рассматривать только движения, происходящие в трёхмерном многообразии точек, а именно на гиперсфере. Поэтому далее необходимо установить проекцию силы Кориолиса на касательное пространство при движении в том же самом касательном пространстве. Для того чтобы построить тензор сил Кориолиса, действующих в касательном пространстве, необходимо сначала построить там какой-либо ортонормированный базис.
В качестве абстрактной модели рассмотрим вращающуюся четырёхмерную гиперсферу единичного радиуса. Возьмём произвольную точку с координатами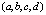 
на этой четырёхмерной гиперсфере. Неявное уравнение гиперсферы 
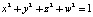, или в следующем виде: 
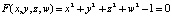. Градиент направлен радиально от центра сферы и равен вектору 
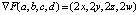, в точке 
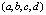соответственно равен 
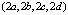. Тогда касательное пространство в точке 
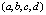задаётся уравнением 
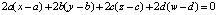, что сводится к виду 
.
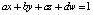Очевидно, в касательном пространстве размерности 3 существует бесконечное множество ортонормированных базисов. Нам достаточно построить какой-либо один из них. Сначала возьмём вектор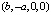 
, заведомо лежащий в касательном пространстве, так как он ортогонален вектору нормали к гиперсфере 
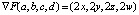. Нормируя его, получаем 
= 
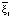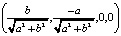. Принимая этот вектор в качестве первого базисного вектора ортонормированного базиса касательного пространства, найдём второй вектор. Он ортогонален как первому вектору, так и градиенту гиперсферы. Тогда его можно найти из двух условий:
.
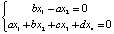В качестве базисного минора можно рассматривать, к примеру, второй и третий столбцы основной матрицы и выразить x2, x3 через x1, x4.
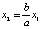. Тогда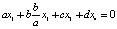 
.
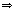
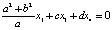
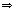
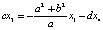Итак,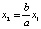 
, 
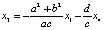, т.е. общее решение есть вектор
.
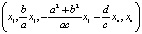Фундаментальная система решений состоит из двух векторов, но при этом, конечно же, нет гарантии, что они ортогональны между собой, поэтому мы возьмём какой-либо один вектор из ФСР, а уже третий (последний) вектор базиса вычислим позже как общий перпендикуляр к двум исходным векторам и нормали к гиперсфере.
При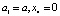 
получается 
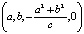. Нормируем этот вектор. Его модуль равен 
= 
= 
.
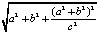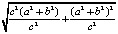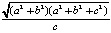Тогда получаем такой единичный вектор
= 
.
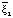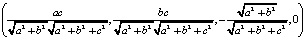Последний вектор ортонормированного базиса найдём как обобщённое векторное произведение трёх векторов:
= 
,
= 
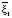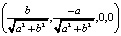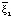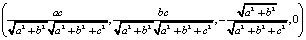
и вектора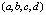 
в четырёхмерном пространстве.
= 
=
= 
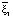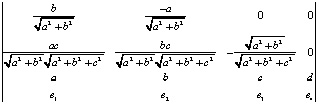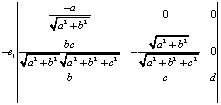
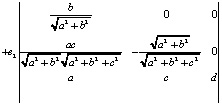
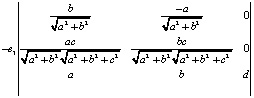
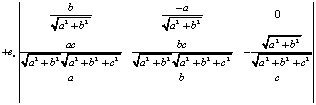
Вычисляя эти определители, получаем четыре координаты вектора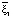 
.
= 
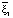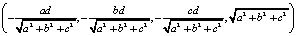
Этот вектор является единичным по построению, как обобщённое векторное произведение трёх единичных векторов.
Итак, мы получили ортонормированный базис из трёх векторов в касательном пространстве к данной четырёхмерной гиперсфере:
= 
= 
= 
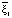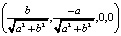
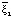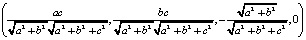
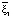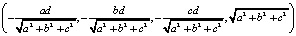
Всякий вектор скорости (v1, v2, v3) в касательном трёхмерном подпространстве выражается в четырёхмерном пространстве в виде: 
. Итак,
+ 
+ 
=
.
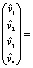
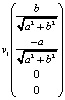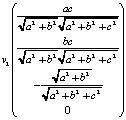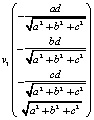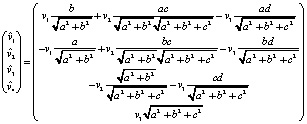При этом для получающегося вектора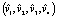 
, сила Кориолиса в расчёте на единичную массу имеет вид
= 
.
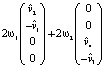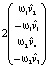Тогда
= 
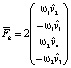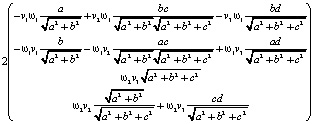
Величина действия данной силы на объекты в трёхмерном пространстве определяется проекцией этой силы на касательное трёхмерное пространство. Поэтому далее необходимо найти проекции полученного вектора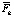 
на все три вектора ранее построенного трёхмерного базиса 
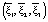. Учитывая тот факт, что базис ортонормированный, нужно найти только скалярные произведения 
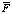на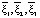 
, делить на квадраты их модулей не нужно. Рассматриваем 
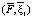как произведение строки на столбец:
= 
=
=
=
.
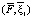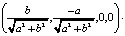
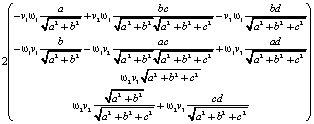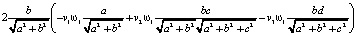
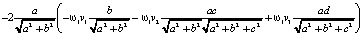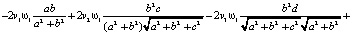
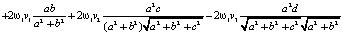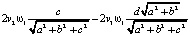Далее, вектор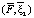 
найдём как произведение строки
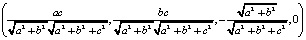
на столбец
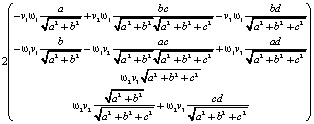
оно равно следующей величине:
= 
.
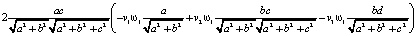
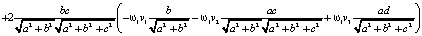
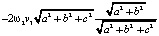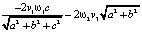Здесь в первых шести слагаемых не взаимоуничтожаются только первые слагаемые из каждой тройки. И наконец,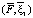 
найдём как произведение строки
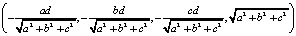
на столбец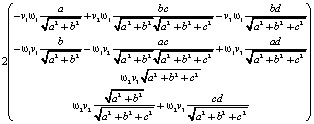 
=
=
.
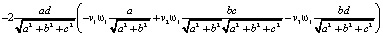
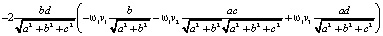
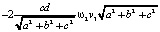
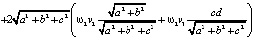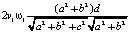
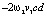
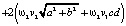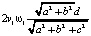
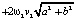Итак, мы получили три величины, которые можно записать в виде вектора-столбца:
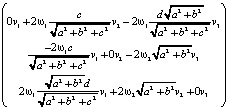
Это проекция вектора силы Кориолиса на касательное пространство к четырёхмерной гиперсфере. Тогда отображение вектора скорости в вектор силы Кориолиса в виде линейного оператора (в расчёте на единичную массу):
.
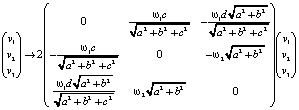Таким образом, тензор сил Кориолиса имеет вид
,
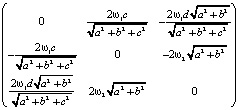то есть он задаётся некоторой антисимметрической матрицей, имеющей структуру:
.
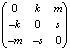Для всякого линейного оператора, имеющего такую структуру, существует единственное действительное собственное значение λ = 0.
= 
= 
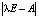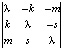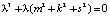, откуда 
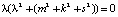, Собственное подпространство, соответствующее собственному значению λ = 0, определяется порождающим его вектором 
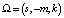, кроме того, существует ортогональное ему двумерное инвариантное подпространство.
Покажем, что выполняется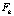 
┴
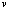. Если 
, 
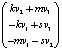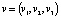, то их скалярное произведение 
.
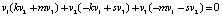Также покажем, что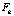 
┴
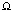. Если 
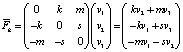, причём 
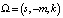, то их скалярное произведение 
.
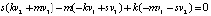Таким образом, на вращающейся четырёхмерной гиперсфере, в каждой точке касательного трёхмерного пространства существует прямая, такая, что при движении тела вдоль неё сила Кориолиса нулевая. При движении в плоскости, ортогональной этой прямой, на тело действует сила Кориолиса, направленная в той же плоскости перпендикулярно движению.
Данный факт может иметь весьма значительные приложения к космологии для объяснения процессов, считающихся необъяснимыми и аномальными на сегодняшний день.
5. Влияние сил Кориолиса на формирование и вращение спиральных галактик
При испускании потоков вещества (при выбросе джета из ядра галактики) в плоскости, перпендикулярной вектору Ω, сила Кориолиса действует продолжительное время на частицы, движущиеся прямолинейно, отклоняя их в направлении, перпендикулярном движению. При выбросе потоков материи из галактического ядра, за длительное время их удаления, силы Кориолиса действуют дольше на дальние части рукавов, в результате чего они приобретают большую тангенциальную скорость. Таким образом, вещество расположится в виде спирали. Чем меньше угол между плоскостью, перпендикулярной оси Ω, и направлением выброса вещества, тем более выражен данный эффект. Возможно, поэтому большинство галактик имеют спиральную структуру. Если выброс вещества происходит вдоль оси Ω, то сила Кориолиса близка к нулю.
В процессе образования спирали, частицы, расположенные дальше от центра галактики, приобрели за счёт силы Кориолиса большую тангенциальную скорость, чем те, которые ближе к центру. При этом сила Кориолиса продолжает действовать, но направлена она уже не по касательной, как было в начале процесса удаления от ядра, а почти к центру галактики, действуя вместе с гравитационной силой. Вспомним, что гравитационная сила, порождаемая массой галактик, в несколько раз меньше той, которая была бы необходима для удержания звёзд и обеспечения наблюдаемого вращения галактик. Аналогично тому, как электромагнитные силы играют роль на малых расстояниях и практически не влияют на движение планет в Солнечной системе, подчиняющееся законам Кеплера, так и гравитационные силы играют малую роль в процессе образования и вращения галактик. Для объектов таких масштабов определяющую роль играют силы Кориолиса, возникающие за счёт вращения Вселенной как четырёхмерной гиперсферы.
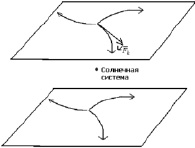
Рис. 3. Иллюстрация асимметричного расположения лево- и правозакрученных галактик
Образовавшиеся из-за воздействия сил Кориолиса галактические рукава закручены в одну и ту же сторону; таким образом, для наблюдателя, находящегося в произвольной точке на планете около одной из звёзд, они будут выглядеть как закрученные влево с одной стороны от плоскости эклиптики и как закрученные вправо с другой стороны от плоскости эклиптики. Именно это и наблюдается в действительности. Более того, вероятно, если изменить условия классификации галактик в проекте Galaxy Zoo, рассматривая две половины небесной сферы не относительно плоскости земного экватора, а относительно плоскости эклиптики, то асимметрия распределения галактик будет ещё более характерно выражена. В видимой нами части Вселенной закручивание галактик под действием сил Кориолиса происходит преимущественно в одну и ту же сторону, аналогично тому, как вихри в земной атмосфере закручены в одну сторону в северном полушарии и в другую – в южном.
Выводы
В рассмотренной абстрактной модели было установлено, что, если движение трёхмерных объектов происходит на вращающейся четырёхмерной гиперсфере, это приводит к появлению дополнительных сил Кориолиса, в результате чего будут наблюдаться следующие явления:
1. При движении потоков вещества, изначально имеющих прямолинейную траекторию (например, выброшенных при взрыве из ядра галактики), сила Кориолиса будет отклонять их, в результате чего потоки вещества постепенно приобретут спиральную структуру.
2. Из любой точки будет наблюдаться анизотропный характер закрученности спиралей окружающих данную точку галактик.
3. Вращение карликовых галактик вокруг крупных будет происходить упорядоченно, несмотря на недостаточность гравитационных сил для таких расстояний.
4. Будет наблюдаться согласованность периодов вращения галактик независимо от их размера и типа. Малые линейные скорости звёзд в малых галактиках соответственно приводят к меньшим значениям сил Кориолиса, что означает прохождение звёзд по окружностям меньших радиусов, но с тем же самым периодом обращения.