Виртуальность – это объект или состояние, которые реально не существуют, но могут возникнуть при определённых условиях. Виртуальный – вероятный, возможный; нечто, что может или должно произойти, проявиться при наличии определенных условий [1].
В работе предпринята попытка показать существование виртуального мира, который может проявлять себя при определенных начальных и граничных условиях в моделях исследуемых и еще не исследованных явлений.
Цель статьи – демонстрация нового способа вычисления произведений целых чисел в уме, основанного на понятии виртуальности, освещение значения виртуальности для нашего трехмерного мира.
Результаты исследования и их обсуждение
Приведём несколько примеров вирту- альности.
1. В арифметике мы встречаемся с понятием виртуальности при умножении первого сомножителя, состоящего из одинаковых цифр, в количестве n1, на второй, состоящий из произвольных цифр, в количестве n2, причём n2 ≤ n1. В этом случае ответ состоит из трёх частей: первой, средней (второй) и последней (третьей) [2].
В нашем случае интерес представляет вторая (средняя) часть. Она состоит из определённого количества периодических цифр (в некоторых случаях со сбоем, т.е. когда последняя цифра этой части на единицу меньше периодической).
Все периодические цифры существуют, но их количество в ответе реализуется в зависимости от величины Δ – разности количества цифр первого и второго сомножителей (Δ = n1-n2), т.е. периодическое число средней части является виртуальным.
Например,
Здесь Δ = n1-n2 = 3, следовательно, количество цифр в
средней части – 3, т.е. 555.
Здесь Δ = 1, и периодическая цифра во второй части
ответа одна, т.е. равна 5.
Заметим, что, зная виртуальные цифры второй части ответа произведений однородных цифр первого сомножителя на второй (n2 < n1), можно записать ответы аналогичных сомножителей, когда n2 > n1 (при n2 = n1; Δ = 0, средней части в ответе нет, но ее можно найти [2]).
Примеры:
а) Вторая часть ответа исходного произведения без сбоя
1) Дано: Найти:
(*) 
Решение:
Среднее периодическое число 44 (Δ = 2).
Согласно [2]:
Здесь ∆ = n2 – n1 = –1,
28 – первая часть ответа. Из (*) имеем 28+1 – 4 = 25. 1 – первое число третьей части ответа. Отрицательная величина Δ указывает на количество отнимаемых виртуальных цифр (число 4) Последняя цифра ответа неизменна во всех случаях.
Получим 8·32 = 256.
(*) 
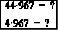
Решение:
Периодическое число средней части 7.
Аналогично предыдущему примеру уменьшаем Δ:
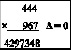
Так как n1 = 2, то в результате
сохраняются две последние
из ответа (*) – 48.
Среднее число 7 отнимается один раз, так как Δ = –1, а 3 – первое число третьей части – прибавляем к первой части ответа (*).
Получим: 429+3 – 7 = 425 – первые цифры ответа, а окончательный ответ: 42548.
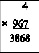Δ = –2; так как n1 = 1, то в ответе сохраняется только одна
последняя цифра 8 (из *). Так как Δ = -2, то отнимаем число,
состоящее из двух виртуальных цифр (77). Получим
429 + 34 – 77 = 386 и окончательный ответ 3868.
3) Дано: Найти:
(*) 
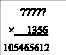
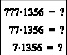
Решение:
При Δ = 0 средняя часть ответа исчезает.
6 – периодическое число средней части.
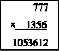Δ = –1. Из (*) имеем: 1054+5 – 6 = 1053. Так как n1 = 3,
то в этом ответе сохраняются три последние цифры
ответа (*). Тогда по аналогии с предыдущими случаями
ответ равен 1053612. (Так как n1 = 3, то в ответе сохраняются 3
последние цифры третьей части.)
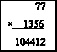Δ = –2. Так как n1 = 2, то сохраняются две последние цифры
третьей части ответа из (*).
К первой части ответа прибавляем две первые цифры третьей
части ответа (56) и отнимаем двучлен из периодических
цифр (66), т.е. 1054+56 – 66 = 1044. Ответ: 104412.
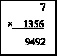Δ = –3. Аналогично предыдущим случаям имеем
1054+ 561 – 666 = 949.
Так как n1 – одна цифра, то в ответе 7×1356 сохраняется
только последняя цифра (2).
б) Ответ исходного произведения содержит сбой в средней части.
Здесь, в отличие от предыдущих случаев, к первой части ответа добавляется слагаемое, представляющее собой разность десятков последнего двучлена средней (второй) части ответа (периодической цифры и цифры сбоя) и числа 10 в случае Δ = –1, при Δ = –2 прибавляется число в 100 раз большее и т.д. и отнимается соответствующее каждому Δ числу виртуальных (периодических) цифр второй (средней) части ответа (*).
Примеры:
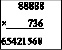
1) Дано: Найти:
(*) 
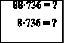
Решение:
Периодическое число средней части ответа (*) равно 2. Её двучлен 21 – со сбоем.
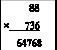Δ = –1. Добавляем число 20 – 10 = 10. Периодическое число,
которое отнимается от первой части ответа произведения
(*) равно 22 и, аналогично, предыдущим случаям
прибавляется при Δ = –1 первая цифра третьей части.
Итак: 654 + 5 + 10 – 22 = 647
Ответ: 64768. Из последних цифр ответа (*) сохраняются две последние, так как n1 = 2 (т.е. число 68).
Δ = –2 n1 = 1. Тогда 654 + 56 + 100 – 222 = 588.
Ответ: 5888 (так как n1 = 1, то сохраняется в ответе одна
цифра из (*).
Δ = 0, n1 = 3. Аналогично методике предыдущих случаев
имеем: 654 + 0 + 1 – 2 = 653
Ответ: 653568 (n1 = 3)
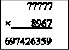
1) Дано: Найти:
(*) 
Решение:
Двучлен средней части ответа (*) 32 – со сбоем.
Периодическое число 3
Решая аналогично предыдущему случаю, получим
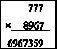Δ = –1; n1 = 3. Тогда 6974 + 6 + 20 – 33 = 6967
(20 = 30 – 10)
Ответ: 6967359
Δ = –2; n1 = 2. Тогда 6974 + 63 + 200 – 333 = 6304
Ответ: 690459
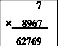Δ = –3; n1 = 1. Тогда 6974 + 635 + 2000 – 3333 = 6276
Ответ: 62769
2. При вычислении неопределённых интегралов ответ обязательно включает произвольную постоянную C.
Например,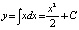 
, где С – const – любое действительное число.
Парабол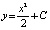 
существует бесконечное множество, а чтобы реализовать необходимую, надо задать соответствующее значение С.
В общем случае все параболы вида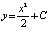 
расположены вдоль оси Oy (от минус до плюс бесконечности), параллельно друг другу симметрично относительно оси Oy. Аналогично для кубической параболы 
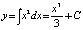, но эти параболы симметричны относительно начала координат, при С = 0. Но с изменением С = const центр симметрии параболы смещается вдоль Oy.
То есть здесь мы имеем реализацию конкретной геометрической фигуры из их бесчисленного множества, задавая соответствующую константу C [3].
3. Класс виртуальных возможностей расширяют дифференциальные уравнения. Здесь мы имеем дело с процессами, протекающими в природе, в различных технических системах. Но здесь мы также имеем дело с неопределенным интегралом, содержащим при вычислении произвольную постоянную С. Её нахождение в этом случае решается другим путем.
Известный пример [3, гл. XIII]:
Пусть с некоторой высоты падает тело массой m. Установить закон изменения скорости падения тела, если на него, кроме силы тяжести, действует сила сопротивления воздуха (пропорциональная скорости) с коэффициентом пропорциональности k, т.е. найти v = f(t).
Решение.
Согласно второму закону Ньютона
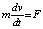, где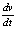 
– ускорение движущегося тела.
Но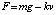 
, где mg – сила тяжести, а kv – сила
Тогда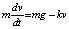 
есть дифференциальное уравнение относительно функции v.
Решить его – значит найти v = f(t), удовлетворяющее данному уравнению.
Таких функций существует бесчисленное множество. Какая же из них реализуется?
Решая это линейное уравнение, получим
. (*)
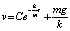Оно удовлетворяет исходному уравнению при любом С = const.
Чтобы найти исходную зависимость v от t, используется дополнительное условие: в начальный момент t = 0, телу была придана известная начальная скорость v0 (которая может быть и равна 0). Тогда v(t) должна быть такой, чтобы при t = 0 выполнялось условие v = v0.
Подставив в решение (*) эти значения, получим
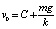или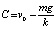 
.
Тогда искомая зависимость (*) имеет вид
.
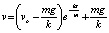Для вакуумной среды (k = 0) получаем v0 + gt.
Подставляя другие начальные условия в это же уравнение (матрица *), получим различные соотношения, удовлетворяющие данному исходному уравнению. То есть возможностей множество, но они реализуются при определенных заданных начальных условиях. Заметим, что в качестве начальных условий в других задачах не обязательно выступает время.
Графически общее решение (*) – это семейство кривых на координатной плоскости, а частное – соответствует конкретному решению С.
Рассмотрим уравнение колебания струны [3]
, (*)
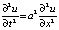где u = u(x, t) описывает процесс колебания струны (величину перемещения струны с абсциссой x в момент времени t);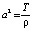 
, где T – натяжение во всех точках струны (силы Т действуют по касательной к струне); ρ – линейная плотность струны. Концы струны закреплены в точках x = 0 и x = l.
Уравнение (*) – волновое уравнение. При его решении получим две произвольные постоянные C1 и C2, а потому u = u(x, t) должна удовлетворять помимо начальных условий, которые заключаются в том, что в начальный момент t = 0 струна имеет определенную форму, которую ей придали (пусть f(x)). Тогда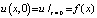 
. Но еще должна быть задана скорость в каждой строчке струны – φ(x), т.е. 
.
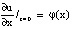Итак, начальные условия для колебаний струны:
.
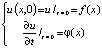Функция u(x, t) должна удовлетворять еще и граничным условиям, указывающим, что делается на концах струны: x = 0 и x = l.
Совокупность граничных и начальных условий называется краевыми условиями.
Множество их вариаций задает множество конкретных реализаций состояния струны, удовлетворяющих общему решению уравнения колебаний. Реализация виртуальности процесса усложняется.
4. В качестве еще одного примера можно привести матрицу систем уравнений Максвелла – Хевисайда – Дятлова, описывающую модель модифицированного физического вакуума (тонкоматериальной субстанции эфира). В ней виртуально содержатся все обозримые качества физического вакуума, каждое из которых можно исследовать, задавая соответствующие начальные и граничные условия и соответствующие коэффициенты [4, 5].
А.Н. Дмитриев утверждает [4, 5]: «Определение вакуумных поляризаций позволило получить первый вариант поляризационной модели неоднородного физического вакуума в виде системы векторных уравнений в частных производных 4-го порядка. Эти уравнения в различных конкретных случаях можно представить в виде самосогласованных (замкнутых) систем уравнений в различных задачах при необходимых начальных и граничных условиях, соответствующих рассмотрению различных физических свойств и особенностей вакуумных доменов».
Заключение
Математика лежит в основе изучения не только нашего вещественного мира, но и позволяет с помощью дополнительных уравнений, описывающих процессы с различными краевыми условиями (при неизменности основных), изучать тонкую (например, эфирную) структуру нашего мира. В частности, это продемонстрировано на примере предложенного устного арифметического способа умножения больших чисел.