Одной из часто решаемых задач в вычислительной геометрии является построение так называемых минимальных выпуклых оболочек (МВО). Данный вид геометрических преобразований используется при анализе и классификации изображений во многих областях науки и техники: в математике, статистике, оптимизации, экономике, геометрическом моделировании и этологии. Из перечисленных отраслей знаний можно выделить более узкие отрасли, где МВО применяются наиболее часто: геодезию и картографию (для ограничения регионов и прочих территорий в геоинформационных системах), материаловедение (с использованием конечных автоматов – для классификации посторонних включений, вызывающих неоднородность строения материалов) [1], системы автоматизированного проектирования (САПР) (реализация триангуляции Делоне и метода конечных элементов – например, для расчёта деталей на прочность, деформации, перемещения), мехатронику и робототехнику (для распознавания образов объектов и определения путей обхода препятствий), кристаллографию (идентификация формы поверхностей кристаллов), организацию компьютерных сетей (в алгоритмах маршрутизации данных), определение оптимального раскроя материала (на заготовительных и производственных участках предприятий) [2]. Технологии создания минимальных выпуклых оболочек используются в исследуемых авторами системах компьютерного зрения роботов [3, 4].
Существует множество алгоритмов обработки изображений с целью получения минимальных выпуклых оболочек [5]: Р. Грэхема (Graham scan), Р. Джарвиса (Gift wrapping algorithm – алгоритм заворачивания подарка), монотонных цепочек Эндрю (Monotone Chain), Чена, алгоритм «Разделяй и властвуй» (Divide and conquer) и, наконец, используемый в данной работе алгоритм QuickHull («быстрого построения») [6], наиболее подходящий для организации быстрых вычислений с помощью программных методов.
Целью данной работы является создание программных средств для вычисления и визуализации минимальных выпуклых оболочек, построенных на плоскости для заданного множества точек i с известными координатами (xi, yi). Код программы должен быть написан на свободно распространяемом, популярном языке Python с использованием библиотеки функций, позволяющей в полной мере реализовать вышеупомянутый алгоритм, – QuickHull.
Созданную программу необходимо апробировать путём расчёта нескольких графических моделей; результаты расчётов следует продемонстрировать путём организации наглядного визуального отображения. Для выполнения всех описанных задач для языка программирования Python имеются наборы функций, оформленные в виде подключаемых библиотек (которые будут рассмотрены далее в статье).
Описываемая разработка дополняет ранее произведённые авторами исследования других типов преобразования и анализа графических систем методами вычислительной геометрии [7].
По результатам выполненной работы необходимо сделать заключение и выводы для дальнейшего применения и развития созданных методов и программных кодов в области обработки изображений.
Материалы и методы исследования
Прежде чем начинать создание программы для отображения рассматриваемого геометрического объекта вокруг заданного множества точек, необходимо сформулировать само понятие минимальной выпуклой оболочки (МВО).
Чтобы осуществить это наиболее наглядно, обратимся к рис. 1.
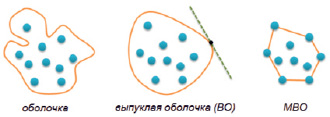
Рис. 1. К объяснению понятий «оболочка», «выпуклая оболочка», «минимальная выпуклая оболочка» (МВО)
Согласно представленным схемам, оболочкой (Convex) называется замкнутая кривая, окружающая все заданные точки. Выпуклая оболочка (Convex hull) – более ограниченное понятие. «Выпуклость» её заключается в том, что любая касательная, проведённая к ней, нигде не пересекает саму оболочку, не заходит внутрь неё. МВО в литературе образно описывают как резиновую ленту, «натянутую» на внешние точки – «шляпки гвоздей» (можно отметить, что данная лента представляет собой траекторию минимальной протяжённости, как бы стянутую вокруг множества точек). При этом все точки рассматриваемого множества либо лежат на МВО, либо внутри неё. Выпуклая оболочка при этом занимает минимальную площадь поверхности (а в трёхмерном случае – минимальный объём пространства).
С МВО связаны и некоторые другие, более сложные и развитые структуры вычислительной геометрии, например на ней основана триангуляция Делоне, диаграммы Вороного. Метод триангуляции Делоне, например, был рассмотрен в статье авторов [8], где продемонстрировано его использование для разбиения геометрических объектов на конечные элементы в системах трёхмерного моделирования (САПР 3D) и расчёта созданных объёмных моделей деталей.
Как было отмечено выше, для программной реализации построения минимальной выпуклой оболочки для заданного множества точек использован язык Python и необходимые в данном случае библиотеки функций. Созданный программный код включает в себя следующую последовательность программных конструкций, автоматически выполняющих определённый набор действий при их запуске:
1. Импорт библиотеки Itertools [9], позволяющей легко создавать так называемые итераторы – сочетания параметров, счётчики, суммирования, размещения, срезы, фильтрации и т.д. Данные итераторы оптимизированы с точки зрения использования минимального объёма памяти компьютера.
2. Импорт модуля Numpy [10], позволяющего организовать эффективную работу со списками и матрицами.
3. Выбор из библиотеки Pyhull [11] функции ConvexHull (выпуклая оболочка).
4. Импорт функций библиотеки Matplotlib.pyplot для вывода на экран графического отображения обрабатываемых точек, соединяющих их линий, а также вычисленной минимальной выпуклой оболочки.
5. Создание массива исходных данных, который последовательно заполняется координатами (xi, yi) исходных точек. Сразу после заполнения массива определяется его длина, и каждая точка помещается на график (пока не выводимый на экран).
6. Применение к массиву точек функции ConvexHull, создающей минимальную выпуклую оболочку в виде графического объекта, который нуждается в проведении ряда операций для его визуального отображения.
7. Для помещения созданной оболочки на график необходимо проделать следующую последовательность операций: для полученного объекта-оболочки с помощью использования атрибута simplices последовательно перебираются все симплексы данного объекта (в данном случае трёхмерные отображения треугольников) и создаются их комбинации (сочетания) с помощью функции Combinations библиотеки Itertools. Каждое такое сочетание образует один из отрезков прямых, составляющих оболочку, и добавляется в ранее созданный массив примитивов оболочки.
8. Создаётся поле графика, границы которого незначительно расширены, исходя из минимальных и максимальных значений координат исходных точек, для получения более совершенной визуализации результатов.
9. На график помещаются примитивы оболочки (напомним, что на него уже нанесены исходные точки). После этого изображение с определёнными в п. 8 границами выводится на экран.
Пример получаемого с помощью программы графика приведён на рис. 2.
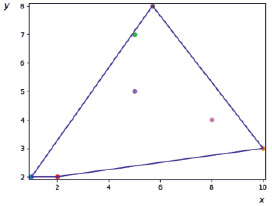
Рис. 2. Результат построения минимальной выпуклой оболочки вокруг точек с заданными координатами
Результаты исследования и их обсуждение
Задачи обработки массивов точек с помощью разработанного программного кода решались для разного количества точек с неизменным получением результатов, соответствующих цели исследования.
Рассмотрим ещё пару примеров, полученных с помощью несколько модифицированного варианта программы. Изменения в коде заключаются лишь в том, что исходные точки изначально составляют массив данных, а затем попарно соединяются в специально организованном для этого цикле, образуя отрезки прямых линий, из которых складывается изображение заданного объекта (и выводится на график). Алгоритм и программный код создания МВО в данном случае остаются неизменными, так как для создания оболочки важны лишь координаты исходного массива точек.
Результаты выполнения программы в этом случае представлены на рис. 3. Чтобы исключить загромождение графиков лишней информацией, сами исходные точки на них не выводятся – последовательно рисуются лишь соединяющие их линии.
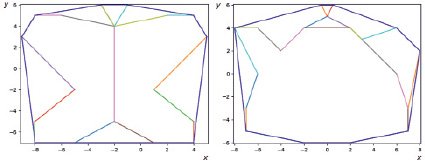
Рис. 3. Результаты выполнения программы, создающей минимальную выпуклую оболочку вокруг объекта из линий
Дальнейшим развитием задач, выполняемых с помощью разработанной технологии, видится создание минимальных выпуклых оболочек для пиксельных бинарных изображений, фактически также состоящих из отдельных точек. Это позволит в каждом случае охарактеризовать характер внешних очертаний изображённых на них геометрических объектов. Такая работа проводилась, например, при идентификации пятен дефектов металлических материалов по схожести построенных минимальных выпуклых оболочек с созданными по образцам эталонными образцами МВО [1].
Однако по приведённым в данной статье иллюстрациям уже видно, что создание минимальной выпуклой оболочки в практическом плане полезно в первую очередь для чёткого очерчивания границ минимальной площади, занимаемой объектом. Это особенно важно для применения в технологиях компьютерного зрения для проведения дальнейших, более детальных операций распознавания образов лишь в данной минимальной по площади зоне, ограниченной МВО.
Также перспективным является применение приведённой методики для отслеживания движения динамических объектов, когда их текущее месторасположение можно описывать лишь отдельными, крайними, точками, лежащими на минимальной выпуклой оболочке. Такие задачи решаются в областях киноиндустрии, военно-оборонных разработок, при создании игровых приложений и в огромном количестве технологических процессов [12] с предполагаемым перемещением деталей или других объектов. Например, в играх таким образом обнаруживаются моменты взаимодействия (столкновения) объектов, когда для повышения производительности реальные очертания объектов заменяются на образы в виде минимальных выпуклых оболочек.
Заключение
Созданные метод и программный код построения минимальных выпуклых оболочек позволяют не только решить упомянутые выше прикладные задачи, но и лучшим, более полным, образом охарактеризовать различные классы реальных физических объектов. Результаты применения метода, представленные в графической форме, являются наглядными и однозначными, кроме того они позволяют охарактеризовать даже очень сложные системы (конечно, только при решении задач, когда внутренняя структура не имеет значения). Перспективно применение минимальных выпуклых оболочек при обработке массивов точек в трёхмерном пространстве.
Описанные методы исследований наглядно демонстрируют преимущества современных компьютерных математических алгоритмов (в частности, реализованных на универсальном языке программирования Python) для моделирования характеристик сложных систем. В описываемом исследовании использована автоматизация математических методов для создания организованных массивов данных и их обработки, организации циклических вычислений, вычисления координат и соединения крайних точек минимальных выпуклых оболочек ConvexHull, работа с комбинациями симплексов и других. Все созданные варианты программ характеризуются простотой кода, быстротой выполнения и наглядностью выводимых в графической форме результатов.
По результатам работы можно сделать вывод, что один из наиболее популярных в мире и, пожалуй, наиболее универсальный язык программирования Python обладает всем необходимым набором модулей для организации обозначенных в целях статьи методов исследования и для их дальнейшего развития и адаптации для использования практически в любой области науки и техники. При этом возможна реализация самых современных математических методов.
Можно рекомендовать детальное изучение применённых и описанных в данной работе математических методик и программных приёмов студентам вузов, инженерам, программистам, учёным и всем лицам, заинтересованным в развитии современных компьютерных технологий.

