Scientific journal

International Journal of Applied and fundamental research

ISSN 1996-3955

ИФ РИНЦ = 0,593

Актуальность исследования обусловлена, с одной стороны, неослабевающей важностью проблемы микробиологической чистоты и профилактики микробной контаминации на фармацевтических и биотехнологических производствах, а с другой стороны, поиском новых возможностей увеличения скорости роста продуцентов и выхода целевого продукта. Избыточное содержание микроорганизмов-контаминантов может вызвать негативные последствия, такие как преждевременная порча готового лекарственного препарата, утрата биологически активных компонентов, трансформация активных веществ, риски для здоровья потребителей. Во избежание этих последствий применяют различные методы воздействия на объекты производственной среды, подверженной контаминации: обработка ультразвуком, различными видами излучений и конвективный нагрев [1]. Все методы имеют существенные недостатки (низкая проникающая способность, низкая эффективность, необходимость контролировать остаточную радиацию, опасность для работающего персонала, изменение физико-химических свойств из-за возникновения термических сопротивлений) [2]. Альтернативой существующим методам обработки материалов с целью улучшения их качества по показателю «микробиологическая чистота» является обработка СВЧ-излучением. Этот метод обладает рядом преимуществ: высокая скорость и равномерность нагрева, экологичность, экономичность за счёт быстроты нагрева, хорошая проникающая способность, эффективность и безвредность для обслуживающего персонала [3]. В процессе исследований по изучению деконтаминирующего действия волн СВЧ-диапазона был отмечен эффект стимулирования роста и активности клеток микроорганизмов при использовании низкоинтенсивного СВЧ-излучения [4, 5]. Учитывая обнаруженный эффект, для определения стимулирующего диапазона воздействия СВЧ-излучения на тестовые микроорганизмы был применен многофакторный эксперимент, важным достоинством которого является его высокая эффективность и достоверное математическое описание объекта [6].

Цель исследования – определение оптимальных диапазонов СВЧ-излучения низкой плотности мощности на рост дрожжей Saccharomyces cerevisiae и Rhodotorula rubra как представителей грибов – объектов биотехнологических исследований.

Материалы и методы исследования

Для обработки СВЧ-излучением низкой плотности мощности использовали культуры дрожжей Saccharomyces cerevisiae ВКМ Y-378 и Rhodotorula rubra ВКМ Y-341. Для проведения многофакторного эксперимента готовили взвеси дрожжей Saccharomyces cerevisiae и Rhodotorula rubra в физиологическом растворе массой 5,00 ± 0,01 г каждая в стеклянных пробирках. Перед обработкой определяли начальную температуру каждой пробирки с культурами (22,1 ± 0,1°С). Для культивирования обработанных и контрольных образцов использовали жидкую питательную среду бульон Сабуро объёмом 25 мл, куда добавляли по 1 мл взвеси дрожжей. Культивирование проводили в колбах объёмом 100 мл, в динамических условиях при частоте вращения колб n = 100 об/мин и температуре 23,0 ± 0,1°С в биореакторе Sartorius Stedim CERTOMAT® CTplus [7]. Для определения концентрации клеток в приготовленных взвесях культур и в культуральной жидкости при выращивании обработанных и контрольных образцов дрожжей, использовали метод прямого подсчёта клеток в счётной камере Горяева [8]. Концентрация взвеси дрожжей для обработки составила 6,7·106 КОЕ/мл. Увеличение биомассы фиксировали через 24 ч от начала культивирования.

Результаты исследования и их обсуждение

Для эксперимента были выбраны факторы: температура нагрева, мощность работы магнетрона и время обработки, уровни варьирования которых отражены в табл. 1.

Обработку проводили при постоянном вакууме (остаточное давление в камере 300 мм рт. ст.), благодаря которому удалось достичь точной воспроизводимости температур обработанных образцов. Значения верхнего и нижнего уровня факторов обработки были выбраны исходя из данных литературных источников. Основной уровень воздействия факторов был рассчитан как среднее арифметическое между верхним и нижним уровнем.

Для выбранных факторов (табл. 1) были определены «звёздные» точки – два уровня варьирования каждым из трёх факторов, значения которых лежат за пределами плана, соответствующего полиному второго порядка для трёх независимых переменных [6]. Результаты расчётов параметров «звёздных» точек показаны в табл. 2.

Далее необходимо удостовериться в том, что выбранная модель проведения многофакторного эксперимента была адекватна. Для этого проводили расчет значения критерия Фишера, который в среднем составил F = 13,534. Значит, уравнение регрессии, которое будет получено на основе рассчитанных данных, будет адекватно описывать процесс в пределах исследуемой области. Далее проводили расчёт критериев Стьюдента для каждого коэффициента регрессии, затем сравнивали их значения со значением табличного критерия Стьюдента для установления его значимости и, возможно, его участия в уравнении регрессии. В результате было получено уравнение регрессии для данного эксперимента в закодированном виде:

y0 = 17,556 – 5,525·x1 – 1,842·x2 – 2,150·x1·x3 – 3,301·x1·x1 – 6,235·x2·x2 – 5,128·x3·x3 . (2)

Уравнение регрессии в раскодированном виде:

а (x,y,z) = 17,556 – 5,525·(0,2·x – 7) – 1,842·(0,003·y – 2) – 2,15·(0,2·x – 7)·(0,5·z – 3) –

– 3,301·(0,2·x – 7)·(0,2·x – 7) – 6,235·(0,003·y – 2) (0,003·y – 2) – 5,128·(0,5·z – 3)·(0,5·z – 3), (3)

где a (x,y,z) = y0 – значения результирующей функции.

После проверки адекватности выбранной модели эксперимента и составления уравнения регрессии определяли уравнения функций отклика при фиксированных значениях варьируемых факторов, а также сами поверхности отклика в виде контурных графиков. В качестве фиксированных значений варьируемых факторов были определены следующие:

х = 30,6°С – фиксированная температура для уравнения функции и поверхности отклика плотности культуры от мощности и времени работы магнетрона;

y = 600 Вт – фиксированная мощность работы магнетрона для уравнения функции и поверхности отклика плотности культуры от температуры нагрева взвеси дрожжей и времени работы магнетрона;

z = 6 c – фиксированное время работы магнетрона для уравнения функции и поверхности отклика плотности культуры от температуры нагрева взвеси дрожжей и мощности работы магнетрона.

Следовательно, уравнение функции отклика при х = 30,6°С будет выглядеть так:

а(y,z) = 17,556 – 5,525·(0,2·30,6 – 7) – 1,842·(0,003·y – 2) – 2,15·(0,2·30,6 – 7)·(0,5·z – 3) –

– 3,301·(0,2·30,6 – 7)·(0,2·30,6 – 7) – 6,235·(0,003·y – 2)·(0,003·y – 2) – 5,128·(0,5·z – 3)·(0,5·z – 3). (4)

График поверхности отклика для функции отклика, указанной в формуле (4), представлен на рис. 1, где показано, что оптимум воздействия СВЧ-излучения низкой плотности мощности на биомассу клеток дрожжей при фиксированной температуре 30,6°С расположен между значениями 5,2 и 7,6 с по шкале времени и между значениями 420 и 810 по шкале мощности.

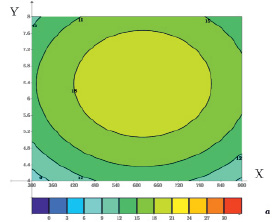
Рис. 1. Поверхность отклика для уравнения функции зависимости плотности культуры от мощности и времени облучения. Y – длительность работы магнетрона, с; X – значения мощности работы магнетрона, Вт; a – значения результирующей функции для данной поверхности отклика, (106) КОЕ/мл

Внутри данного оптимума прирост биомассы клеток дрожжей достигал 18,0·106 КОЕ/мл, что больше прироста биомассы в контроле в 2,1 раза.

Далее определили уравнение функции отклика при y = 600 Вт:

а(x,z) = 17,556 – 5,525·(0,2·x – 7) – 1,842·(0,003·600 – 2) – 2,15·(0,2·x – 7)·(0,5·z – 3) –

– 3,301·(0,2·x – 7)·(0,2·x – 7) – 6,235·(0,003·600 – 2)·(0,003·600 – 2) – 5,128·(0,5·z – 3)·(0,5·z – 3). (5)

График поверхности отклика для функции отклика, указанной в формуле (5), представлен на рис. 2, где показано, что зона оптимума воздействия факторов так же, как и на рис. 1, имеет вид замкнутой окружности и ограничена значениями 5,2 и 7,6 с по шкале времени и 26,5 и 35,0°С по шкале температуры.

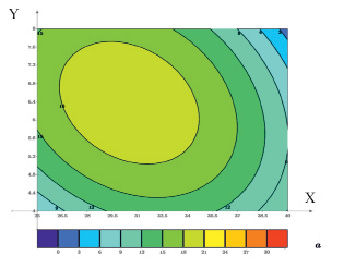
Рис. 2. Поверхность отклика для уравнения функции зависимости плотности культуры от температуры нагрева взвеси дрожжей и времени обработки. Y – длительность работы магнетрона, с; X – значения температуры нагрева взвеси дрожжей, °С; a – значения результирующей функции для данной поверхности отклика, (·106) КОЕ/мл

Внутри данного оптимума так же, как и в случае с графиком на рис. 1, прирост биомассы может достигать 18,0·106 КОЕ/мл.

После этого определили уравнение функции отклика при z = 6 c:

а(x,y) = 17,556 – 5,525·(0,2·x – 7) – 1,842·(0,003·y – 2) – 2,15·(0,2·x – 7)·(0,5·6 – 3) –

– 3,301·(0,2·x – 7)·(0,2·x – 7) – 6,235·(0,003·y – 2)·(0,003·y – 2) – 5,128·(0,5·6 – 3)·(0,5·6 – 3). (6)

График поверхности отклика для функции отклика, указанной в формуле (6), представлен на рис. 3, из которого видно, что зона оптимума воздействия факторов представляет собой окружность, внутри которой прирост биомассы по расчётам может достигать 18,0·106 КОЕ/мл.

При этом в центре этой зоны оптимума расположена точка, соответствующая приросту биомассы 20,0·106 КОЕ/мл. По оси значений мощности работы магнетрона зона оптимума ограничена величинами 420 и 780 Вт, а по оси значений температур нагрева величинами 27,3 и 36,3°С (рис. 3).

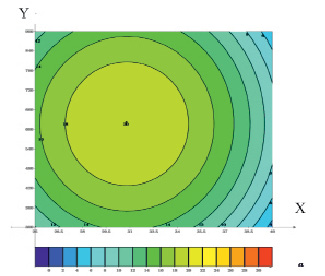
Рис. 3. Поверхность отклика для уравнения функции зависимости плотности культуры от температуры нагрева взвеси дрожжей и мощности работы магнетрона. Y – значения мощности работы магнетрона, Вт; X – значения температуры нагрева взвеси дрожжей, °С; a – значения результирующей функции для данной поверхности отклика, (·106) КОЕ/мл

Заключение

Применение многофакторного эксперимента позволило установить оптимальные параметры воздействия СВЧ-излучения низкой плотности мощности на активацию роста клеток дрожжей Saccharomyces cerevisiae: мощность работы магнетрона от 420 до 780 Вт, температура нагрева взвеси дрожжей от 26,5 до 36,3°С, время работы магнетрона от 5,2 до 7,6 с. При воздействии СВЧ-излучения в данных диапазонах достигнуто увеличение концентрации клеток дрожжей в 2,1 раз по сравнению с контрольным образцом. С учётом особенностей работы установки для СВЧ-обработки и для проведения дальнейших экспериментов по изучению воздействия СВЧ-излучения низкой плотности мощности в пределах зоны оптимума на клетки дрожжей Sac. cerevisiae и Rh. rubra были выбраны следующие оптимальные параметры работы установки: мощность излучения 600 Вт, температура разогрева взвеси дрожжей от 26,0 до 35,0°С, время обработки от 5 до 8 с. Полученные результаты могут быть учтены при обработке микроорганизмов-продуцентов в фармацевтических и биотехнологических производствах для усиления их активности и получения больших выходов целевых продуктов.