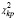Статистическая обработка данных зачастую связана с исследованием свойств случайных величин, характеризующих те или иные особенности изучаемого объекта. Важной характеристикой, которая несет в себе максимально возможный объем полезной информации об изучаемых случайных величинах, является функция плотности распределения. Следовательно, задача восстановления функции плотности по имеющимся статистическим данным является очень актуальной. Существуют различные методы для ее решения, в частности метод, основанный на вейвлет-анализе [1, 2], который на сегодняшний день динамично развивается и широко применяется для аппроксимации различных функций [3, 4]. Ранее такой подход был реализован с использованием вейвлетов Хаара, DOG, «Мексиканская шляпа» и Литлвуда – Пэли [5–7], а проведенные исследования подтвердили его эффективность. В данной работе исследуются вейвлет-оценки функции плотности распределения, построенные на основе вейвлета Морле.
Для этого рассмотрим выборку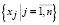 
, заданную на произвольном отрезке [c, d] , где 
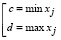. Выборка состоит из независимых значений случайной величины ξ. Отметим, что информации о функции плотности распределения f(t) случайной величины ξ не имеется. Необходимо построить вейвлет-оценку f̂n(t) плотности распределения на основе имеющихся данных.
Вейвлет-оценки функции плотности распределения
Вейвлет-оценка функции плотности распределения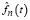 
случайной величины, согласно [1, 2] может быть представлена в виде следующего ряда:
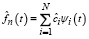, (1)
где ψi(t) – ортонормированные базисные функции, N – параметр сглаживания (количество членов ряда),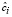 
– коэффициенты разложения, которые выражаются следующим соотношением:
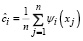. (2)
Если подставить (2) в выражение (1), то получим вейвлет-оценку функции плотности распределения в следующем виде
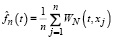, (3)
где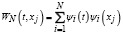 
.
В роли базисных функций ψi(t) можно выбрать предложенную в [1, 2] систему функций, которая ортонормирована на отрезке [0, 1] и определяется следующим образом:
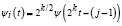, (4)
где ψ(t) – материнский вейвлет, k ≥ 0, 1 ≤ j ≤ 2k и i = 2k + j. Отметим, что выражение (4) выполняется для всех i > 1, а в случае i = 1 полагают, что ψ1(t) = 1 для всех t ∈ [0, 1], иначе ψ1(t) = 0.
Так как выбранная система базисных функций ψi(t) определена на отрезке [0, 1], необходимо выполнить переход к ортонормированной системе функций ψ̃i(t) заданной на отрезке [c, d], который соответствует области определения случайной величины ξ.
Согласно [5–7] переход от одной системы базисных функций к другой выражается следующим соотношением
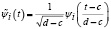. (5)
Тогда вейвлет-оценка функции плотности распределения f̂n(t) на произвольном отрезке [c, d] определяется выражением (3), где в качестве базисных функций используются функции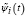 
.
Согласно определению ортонормированной системы функций [1, 2] система базисных функций ψi(t) должна удовлетворять двум условиям:
1) 
,
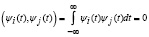для всех i ≠ j;
2) 
.
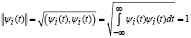Следовательно, из соотношения (4) и свойств нормы материнского вейвлета [2] получаем
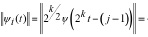
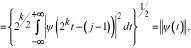(6)
где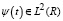 
.
Таким образом, выполнение этих условий семейством ψi(t) зависит от выбора порождающего их материнского вейвлета ψ(t). Если материнский вейвлет ортонормированный, то и система функций ψi(t) также будет являться ортонормированной.
Перейдем к исследованию вейвлет-оценки функции плотности (3), где в качестве материнского вейвлета выбран вейвлет Морле [8–10].
Оценивание функции плотности распределения с помощью материнского вейвлета Морле
Аналитическая запись материнского вейвлета Морле [8–10] определяется соотношением
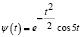. (7)
Тогда система функций (4) на отрезке [0, 1] выражается следующим образом:
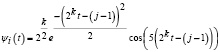, (8)
где i, k, j такие же, как в (4). Известно, что материнский вейвлет Морле является ортогональным [2, 8–10]. Покажем, что вейвлет Морле не является нормированным, как следствие, система функций (8) тоже.
Утверждение 1. Пусть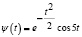 
– материнский вейвлет Морле, порождающий систему функций 
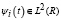, которая принимает вид
,
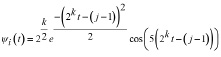где k ≥ 0, 1 ≤ j ≤ 2k и i = 2k + j. Тогда для любых i, k, j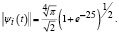 
Доказательство.
Аналитическая запись материнского вейвлета Морле выражается соотношением
.
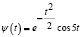Тогда по определению нормы в L2(R) получаем
.
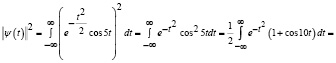
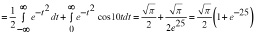Поскольку для любых k ≥ 0, 1 ≤ j ≤ 2k, где i = 2k + j выполняется равенство (6), то норма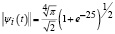 
. Утверждение доказано.
Отсюда следует, что базис (4) на основе материнского вейвлета Морле не нормирован: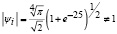 
. В соответсвии с [2, 8] такая система базисных функций может быть использована для построения (3), если ввести нормировочный множитель 
.
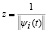Тогда система функций (8) становится ортонормированной и принимает вид
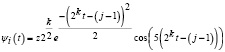, (9)
где i, k, j аналогичны (4),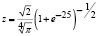 
.
С учетом (9) переход от отрезка [0, 1] к отрезку [c, d], который соответствует области определения наблюдаемой случайной величины, дает результат
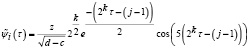, (10)
где i, k, j аналогичны (4),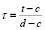 
.
Тогда выражение (3), где в качестве базисных функций используются функции (10), является вейвлет-оценкой функции плотности распределения f̂n(t) на произвольной области определения [c, d] на основе материнского вейвлета Морле.
Исследование точности вейвлет-оценки на основе вейвлета Морле
С помощью серии вычислительных экспериментов была исследована точность вейвлет-оценки на основе материнского вейвлета Морле. Для этого были смоделированы выборки из независимых значений случайной величины ξ объемом n = 300; 500; 1000. Распределение случайной величины ξ соответствует стандартному нормальному закону. Для данных выборок было выполнено оценивание функции плотности распределения с помощью вейвлета Морле при изменении числа членов ряда N от 4 до 40. На рис. 1 представлены результаты оценивания функции плотности для выборки объемом n = 1000 при N = 5; 15; 25. Качество оценивания f(t) напрямую зависит от параметра сглаживания. Если количество членов ряда оказывается недостаточным, то вейвлет-оценка не соответствует исходной функции плотности распределения из-за существенного отклонения. Если количество членов ряда велико, то оценка функции f̂n(t) имеет дополнительные максимумы и минимумы, что никак не соответствует модельной плотности распределения. Как в первом, так и во втором случае восстановленная функция плотности достаточно сильно отличается от истинной. Таким образом, в ходе вычислительных экспериментов было получено наилучшее значение параметра сглаживания для вейвлета Морле N = 5. Результаты моделирования для выборок с меньшими объемами n = 300; 500 подтвердили приведенные выше выводы.
Найденное выше значение параметра сглаживания N = 5 было использовано для исследования точности восстановления функции плотности от объема выборки n. Для этого были построены вейвлет-оценки (3) на основе материнского вейвлета Морле для рассматриваемых ранее выборок объема n = 300; 500; 1000. На рис. 2 представлены полученные результаты.
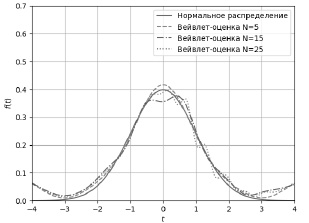
Рис. 1. Результаты оценивания функции плотности с помощью вейвлета Морле
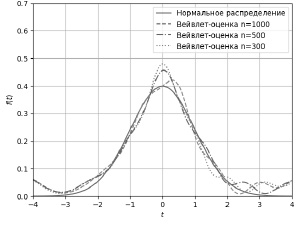
Рис. 2. Результаты оценивания функции плотности с помощью вейвлета Морле
Значение статистики χ2
|
n |
T |
|
χ2 |
|
|
α ≤ 0,05 |
α ≤ 0,01 |
|||
|
300 |
8 |
14,067 |
18,475 |
10.589 |
|
500 |
10 |
19,919 |
21,666 |
11.413 |
|
1000 |
11 |
18,307 |
23,209 |
11.884 |
Эти вычислительные эксперименты подтвердили предположение о том, что объем данной выборки влияет на точность восстановления функции плотности. Из рис. 2 видно, что выборки с наименьшим объемом имеют наибольшую величину отклонения истинной функции плотности распределения от её оценки.
Отметим, что подобные исследования вейвлет-оценок на основе вейвлет Морле проводились для выборок, состоящих из случайных величин, имеющих другие законы распределения, в частности рассматривалось гамма распределение и экспоненциальное с параметром λ = 2. Результаты моделирования также показали, что с увеличением объема выборки точность вейвлет-оценки повышается.
Поверка степени близости между истиной функцией плотности распределения и ее оценкой для 1000 выборок объема n = 300; 500; 1000 состоящих из множества независимых значений случайной величины ξ, была проведена по критерию χ2 [11]:
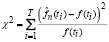, (11)
где T – число интервалов, полученное с помощью формулы Стерджеса [11], ti – середина i-го интервала. В таблице приведены критические значения критерия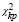 
при числе степеней свободы v = T – 1 для α ≤ 0,05 и α ≤ 0,01. Также в таблице представлены результаты, из которых видно, что значения величины χ2 намного меньше 
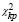, что подтверждает близость вейвлет-оценки 
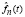и теоретической функции плотности f(t).
Аналогичным образом была выполнена оценка степени близости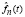 
и f(t) для случайных величин, имеющих другие законы распределения, а именно гамма распределение и экспоненциальное с параметром λ = 2. Результаты моделирования подтвердили работоспособность данного метода оценивания.
Заключение
В работе была рассмотрена оценка функции плотности распределения случайной величины на основе вейвлета Морле. Сформулировано и доказано утверждение о том, что данный материнский вейвлет является ненормированным, следовательно, и система базисных функций, построенная с его помощью. Получено значение нормировочного множителя, которое позволяет улучшить качество восстановления функции плотности. Установлено, что качество оценки функции плотности существенно зависит от параметра сглаживания и в ходе вычислительных экспериментов получено его наилучшее значение. Показано, что объем выборки оказывает влияние на качество восстановления функции плотности распределения. В частности, в случае малого объёма выборки наблюдается большее отклонение вейвлет-оценки плотности распределения от теоретической функции плотности. Поверка по критерию хи квадрат количественной степени близости между истиной функцией плотности распределения и ее оценкой показала, что выбор вейвлета Морле в роли базового обеспечивает качественное восстановление функции плотности.