Любой современный механизм состоит из твердых тел, объединенных в одну общую систему. Главное назначение данной системы – преобразовывать движение одного или нескольких твердых тел в необходимые движения других твердых тел. Строение (структура) механизмов может иметь как простое, так и довольно сложное исполнение. В прямой зависимости от строения (структуры) механизма находятся выполняемые им движения, варианты преобразования этих движений, а также количество степеней свободы. Наложение связей – неотъемлемая часть соединения отдельных звеньев в механизм. От правильного выбора и распределения этих связей зависят надежность и работоспособность механизма. В связи с этим фактом очень важно знать основные виды и структуру (закономерности их строения) современных механизмов [1, 2].
Цель исследования – на этапе проектирования определить энергетические параметры привода, обеспечивающие требуемый уровень надежности функционирования систем лесных машин, и тем самым сократить объем конструкторско-доводочных испытаний и затраты на разработку.
Материалы и методы исследования
Наложение связей сопровождает формирование механизма, то есть позволяет соединить отдельные его части в единую систему. Надежная эксплуатация в значительной степени определяется правильным их распределением в строении механизма. Для этого при проектировании нужно из множества разнообразных механизмов выбрать самый подходящий и правильно подобрать его основные структурные элементы [3, 4].
Изменение взаимного положения в пространстве материальных тел или положение частей данного тела определяется строением механизма. Звенья в механизме соединяются с помощью кинематических пар разного вида в зависимости от числа связей, накладываемых на относительное движение звеньев. Эти варианты анализируются на основе структурной схемы механизма, которая может быть представлена назначения.
Результат срабатывания многих механических систем – перемещение подвижной части из некоторого начального положения в конечное, определяемое конструктивной схемой. Очевидно, достижение подвижной частью заданного конечного положения может служить критерием безотказности функционирования такой системы [5, 6]. В этом случае надежность системы может быть оценена вероятностью выполнения условий срабатывания:
Нф = Р{x = xk}.
Проведение расчетов по данному соотношению возможно методом статистических испытаний (метод Монте-Карло) с использованием известных формул математической статистики [7]. Однако применение этого метода для подтверждения вероятности безотказной работы высоконадежных систем требует расчета большого количества реализаций процесса перемещения. Более глубокую информацию о вероятностных свойствах системы можно получить из исследования модели процесса функционирования и выработки соответствующих условий безотказности [8, 9].
Результаты исследования и их обсуждение
Функционирование системы (процесс перемещения ее подвижной части) характеризуется соотношением движущих сил Fдв(х), развиваемых соответствующим приводом, и сил сопротивления движению Fс(х), наличие которых обусловлено конструктивной схемой. При этом часть энергии привода идет на преодоление сил сопротивления на участке перемещения, а ее избыток переходит в кинетическую энергию подвижных частей.
Очевидно, для того чтобы происходил процесс перемещения, достаточно выполнения неравенства Fдв(х) > Fс(х) на всем участке перемещения [0, xk]. Вероятность выполнения этого неравенства может служить оценкой надежности функционирования системы [10]:
Нф = Р{Fдв(х) > Fс(х); 0 ≤ x ≤ xk},
где Fдв(х), Fс(х) – случайные функции своего аргумента (в общем случае).
Однако оценка надежности по последней формуле получается заниженной, так как при этом не учитывается возможность перемещения подвижных частей за счет накопленной кинетической энергии даже в случае превышения сил сопротивления над силами привода. По-видимому, при расчете надежности в качестве параметров функционирования, наиболее полно характеризующих процесс перемещения, следует рассматривать функции работы действующих сил по пути перемещения. При этом надежность определяется как вероятность того, что работа движущих сил системы Aдв(х) превысит работу сил сопротивления Aс(х) на всем пути перемещения, т.е.
Нф = Р{Aдв(х) > Aс(х); 0 ≤ x ≤ xk},
где
;
.
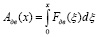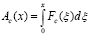Для расчета надежности функционирования механических систем можно использовать два метода.
Аналитический метод. Для решения поставленной задачи преобразуем выражение
Нф = Р{A(х) > 0; 0 ≤ x ≤ xk}, (1)
где
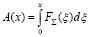; FΣ(ξ) = Fдв(ξ) – Fс(ξ).
Таким образом, мы пришли к задаче о нахождении вероятности превышения нулевого уровня случайным процессом A(х) на пути [0, xk]. В общем случае эта задача решена в [10]. Согласно этой работе для Нф можно записать следующую оценку снизу:
,
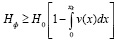где H0 – вероятность безотказной работы системы в начальный момент движения;
v(х) – математическое ожидание числа пересечений нулевого уровня в единицу времени.
Выражения для H0 и v(х) в общем случае можно записать следующим образом:
H0 = Р{FΣ(0) > 0}; (2)
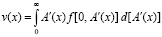, (3)
где A’(х) = FΣ(x) – производная функция работы А(х);
f(0, A’(х)) – совместная плотность распределения А(х) и A’(х) в точке А(х) = 0.
Как правило, на практике известны вероятностные характеристики процесса FΣ(x): математическое ожидание mF(x) и корреляционная функция kF(x1, x2). Тогда, согласно [10], соответствующие характеристики для А(х) могут быть определены из выражений
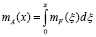; (4)
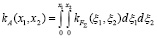, (5)
а их взаимная корреляционная функция
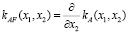. (6)
В частном случае, когда процесс FΣ(x) стационарен, вместо (5, 6) будем иметь
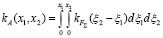; (7)
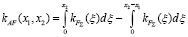. (8)
Полагая в последнем равенстве х = х1 = х2, получим выражения для дисперсии
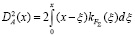(9)
и взаимного корреляционного момента
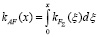. (10)
По соотношениям (2)–(10) фактически можно решать задачу определения надежности функционирования широкого класса механических систем.
Характер изменения функции v(x), полученный для нормального стационарного процесса с характеристиками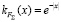 
, 
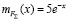, 0 ≤ x ≤ I, представлен на рис. 1. Проведенные исследования показали, что в окрестности нуля v(x) ведет себя как функция x–1/2, чем объясняется резкое убывание v(x) в начале координат. Возрастание v(x) при х > 0,1 связано с уменьшением избыточности по силе при перемещении подвижной части системы.
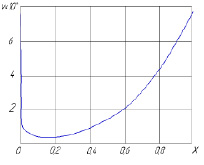
Рис. 1. Изменение функции v(x) при нормальном стационарном процессе
Метод статистического моделирования минимума параметрической функции. Для расчета надежности вторым способом преобразуем выражение (1) к виду
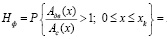
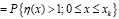, (11)
где η(x) = Aдв(х) / Aс(х) – коэффициент энергетического запаса системы. Для η(x) в точке х = 0 получаем
.
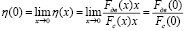Таким образом, функция может быть определена на всем участке перемещения [0; хk].
Событие, состоящее в том, что минимум процесса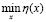 
на интервале [0; хk] больше уровня а = 1 (рис. 2) эквивалентно событию, заключающемуся в том, что на участке 0 ≤ x ≤ xk процесс η(x) не выйдет за уровень а. Следовательно, соотношение (II) эквивалентно выражению
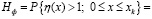
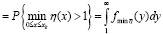, (12)
где fmin η(y) – функция плотности распределения случайной величины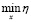 
[5].
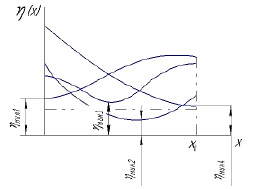
Рис. 2. Зависимость реализации процесса η(x) по пути перемещения х
Плотность распределения fmin η(y) определяется по выборке значений случайной величины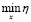 
. При этом для каждой реализации возмущающих воздействий Fдв(х) и Fс(х) находятся реализации процесса η(x) по пути перемещения х и выбираются соответствующие им значения 
.
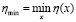На практике часто встречается случай, когда Fдв(х) является монотонно убывающей случайной функцией х, a Fс(х) – случайной функцией, не зависящей от х. В этом случае надежность функционирования может быть оценена по формуле
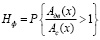, (13)
где
;
;
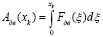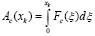Fдв(х) = φ(x,b,c,…), Fс = d; b,c,…d – случайные величины, не зависящие от х.
Справедливость выражения (13) подтверждается исследованиями функции η(x), которая при принятых условиях является убывающей функцией своего аргумента, достигающей минимума при х = хk. Таким образом, учитывая соотношение (12), получаем
.
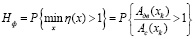Для практических расчетов это выражение целесообразно представить в виде
Нф = Р{Aдв(хk) – Aс(хk) > 0} = Р{A(хk) > 0},
где
A(хk) = Aдв(хk) – Aс(хk).
При нормальном законе распределения случайных величин Aдв(хk), Aс(хk)
,
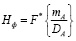где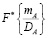 
– функция нормированного распределения [6];
;
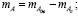
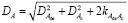где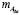 
, 
, 
, 
, 
, 
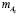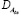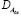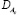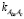– соответственно математические ожидания, средние квадратические отклонения и взаимный корреляционный момент случайных величин Aдв(хk), Aс(хk).
Нетрудно убедиться, что если Fдв(х) – монотонно возрастающая случайная функция, то надежность можно оценить по формуле
Нф = Р{Aдв(0) – Aс(0) > 0}
Заключение
Рассмотренные методы позволяют достаточно просто и принципиально точно оценить надежность функционирования однозвенных пружинно-шарнирных механизмов, замков и толкателей. При этом возможно уже на этапе проектирования определить энергетические параметры привода, обеспечивающие требуемый уровень надежности функционирования системы и тем самым сократить объем конструкторско-доводочных испытаний и затрат на разработку.