Дискретные динамические модели образуются при моделировании дискретных процессов [1] или при дискретизации непрерывных моделей [2], а также при моделировании многих технических, экономических задач и задач автоматического управления, в которых используются дискретные модели оптимального управления [3–5].
Такая необходимость вытекает из всеобщей цифровизации общества. Это означает, что цифровые устройства, информацию получают или передают в дискретные моменты времени. В связи со сложностью построения аналитических решений дискретных задач оптимального управления, широко используется асимптотический метод построения решений таких задач [6, 7].
Цель данной работы состоит в построении асимптотического алгоритма решений линейной сингулярно-возмущенной дискретной задачи оптимального управления с малым шагом. Сингулярно-возмущенные системы дифференциальных уравнений в настоящее время активно развиваются и применяются для решения широкого круга задач в различных отраслях науки [8–10]. Такие системы появляются естественным образом в процессе моделирования и исследования объектов различной природы, способных одновременно совершать быстрые и медленные движения [8–10]. В связи с этим актуальной является задача разделения медленных и быстрых движений системы. Построению оптимальных решений в задачах с разнотемповыми динамическими системами с разделением движений посвящено множество работ, а именно в сингулярно-возмущенных системах [8–11] и в дискретных задачах оптимального управления [12–14]. Данная работа является продолжением исследований дискретной задачи оптимального управления.
1. Алгоритм решений задачи
В этом разделе вводим разностное сингулярно-возмущенное уравнение с –постоянными матрицами. Сначала формулируется условие, необходимое для выполнения исследуемой системы.
1.1. Постановка задачи
Объект управления описывается разностным уравнением
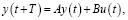 (1)
(1)
где
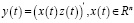 ,
, 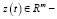 векторы переменных состояния,
векторы переменных состояния,
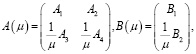
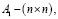
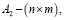
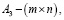
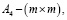
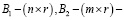 постоянные матрицы,
постоянные матрицы, 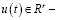 вектор управления,
вектор управления, 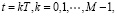
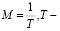 малый шаг, 0 ≤ Т ≤ 1, μ – малый параметр, 0 < μ < 1, штрих обозначает транспонирование.
малый шаг, 0 ≤ Т ≤ 1, μ – малый параметр, 0 < μ < 1, штрих обозначает транспонирование.
Систему (1) перепишем в виде
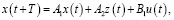 (2)
(2)
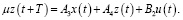
Для системы (1) заданы начальные и конечные состояния:
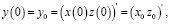 (3)
(3)
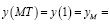
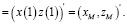 (4)
(4)
Предположим выполнения для системы (1).
Условие 1. Собственные значения матрицы А4 удовлетворяют неравенству
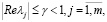
где γ – некоторая постоянная.
При выполнении условия (1), рассмотрим задачу минимизации функционала
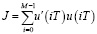 (5)
(5)
при ограничениях (2)–(4).
Как показано в [10, 13, 14], используя замены
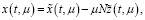 (6)
(6)
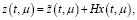 (7)
(7)
из системы (2) получаем
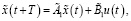 (8)
(8)
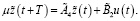 (9)
(9)
где
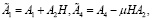 (10)
(10)
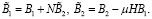
Матрицы H и N имеют размерности m × n и n × m соответственно и удовлетворяют следующим матричным уравнениям Риккати и Ляпунова [8, 10, 14]:
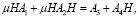 (11)
(11)
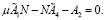 (12)
(12)
Уравнения (11), (12) имеют решения в виде равномерно сходящихся степенных рядов [8, 10, 14]:
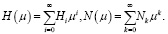 (13)
(13)
Матрицы Hi(μ) и Nk(μ) (i,k = 0,1,…) определяются путем приравнивания коэффициентов при одинаковых степенях μ в уравнениях (11), (12). В результате имеем [8, 10, 14]:
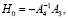
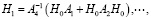 (14)
(14)
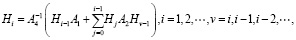
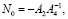
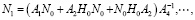 (15)
(15)
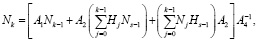
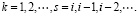
Граничные условия системы (8) и (9) определяются соотношениями
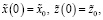 (16)
(16)
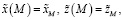 (17)
(17)
где
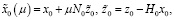 (18)
(18)
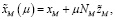
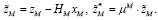 (19)
(19)
В результате получили систему, состоящую из двух уравнений (8) и (9), которые решаются независимо друг от друга.
1.2. Вывод формулы задачи
Теперь рассмотрим задачу (5), (8)–(10), (16)–(19). Для системы (8), (9) предположим выполнение следующих условий:
Условие 2. Матрицы 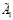 и
и 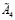 являются матрицами простой структуры и не имеют нулевых собственных значений λs
являются матрицами простой структуры и не имеют нулевых собственных значений λs 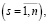 γk
γk 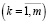 соответственно.
соответственно.
Условие 3. Для собственных значений λs 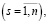 γk
γk 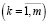 матрицы
матрицы 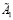 и
и 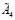 выполняются следующие ограничения:
выполняются следующие ограничения:
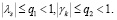
По второму условию матрицы 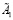 и
и 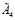 не имеют нулевых собственных значений, тогда собственные значения матрицы
не имеют нулевых собственных значений, тогда собственные значения матрицы 
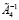 соответственно равны
соответственно равны 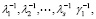
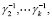 а соответствующие их собственные векторы совпадают с собственными векторами
а соответствующие их собственные векторы совпадают с собственными векторами
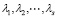 и
и 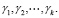
Решения системы (8), (9) с начальными условиями (16), (18) представим в виде
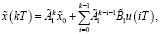 (20)
(20)
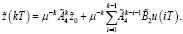 (21)
(21)
C учетом конечных условий (17), (19) из (20) и (21) имеем
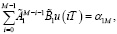
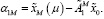 (22)
(22)
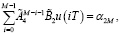
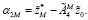 (23)
(23)
На основании теории проблемы моментов [8, 15] соотношения (22) и (23) выражают необходимые и достаточные условия, которые должны удовлетворять функция 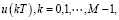 чтобы системы (8), (9) переводились из заданного начального состояния (16) в заданное конечное состояние (17) [8, 15]. Кроме того, функция u(kT) должна доставлять минимум функционалу (5). Однако движения системы (8) и (9) являются разнотемповыми. В связи с этим совместное решение уравнений (22) и (23) не является возможным [8, 15]. Так как для того, чтобы быструю подсистему (9) переводить из заданного начального состояния (16) в конечное состояние (17), необходимо найти функцию u(kT), удовлетворяющую уравнению (23), а также найденная функция u(kT) выражается через обратную матрицу и возникает требование ее существования при
чтобы системы (8), (9) переводились из заданного начального состояния (16) в заданное конечное состояние (17) [8, 15]. Кроме того, функция u(kT) должна доставлять минимум функционалу (5). Однако движения системы (8) и (9) являются разнотемповыми. В связи с этим совместное решение уравнений (22) и (23) не является возможным [8, 15]. Так как для того, чтобы быструю подсистему (9) переводить из заданного начального состояния (16) в конечное состояние (17), необходимо найти функцию u(kT), удовлетворяющую уравнению (23), а также найденная функция u(kT) выражается через обратную матрицу и возникает требование ее существования при 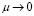 [8, 15].
[8, 15].
Поэтому для подпространства переменных состояния 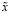 и
и 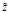 необходимо выбрать оптимальное управление, в котором каждое уравнение (22) и (23) решается независимо друг от друга относительно неизвестных параметров.
необходимо выбрать оптимальное управление, в котором каждое уравнение (22) и (23) решается независимо друг от друга относительно неизвестных параметров.
Исходя из этих требований оптимальное управление будем искать в виде
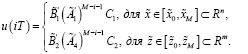 (24)
(24)
Подставляя (24) в (22) и (23), получаем уравнения
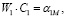 (25)
(25)
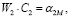 (26)
(26)
где
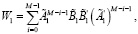
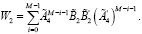 (27)
(27)
Матрицы W1 и W2 положительно определенные [8, 10], следовательно, оптимальные управления и соответствующие оптимальные траектории для системы (8) и (9) определяются в формах
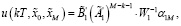 (28)
(28)
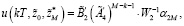 (29)
(29)
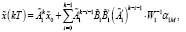 (30)
(30)
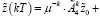
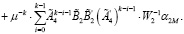 (31)
(31)
1.3. Алгоритм решений задачи
Исходя из полученных формул алгоритм решений задачи (1)–(5) состоит в следующем:
1) вводится массив исходных данных системы (1): матрицы 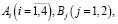 начальные и конечные условия x0, xM, z0, zM период квантования T, количество шагов M, μ – малый шаг;
начальные и конечные условия x0, xM, z0, zM период квантования T, количество шагов M, μ – малый шаг;
2) проверяется выполнения условий 1. Если условие 1 выполняется переход осуществляется к пункту 3, иначе к пункту 1;
3) по формулам (13)–(15) определяются матрицы H и N;
4) проверяются подстановкой матриц H и N в уравнения (11) и (12) соответственно. Если матрицы H и N удовлетворяют уравнения (11) и (12), то переход осуществляется к пункту 5, иначе к пункту 3;
5) по формулам (10) определяются матрицы: 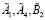 и
и 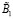 ;
;
6) проверяется выполнения условий 3 для матрицы 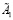 и
и 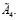 Если условие 3 выполняется, переход осуществляется к пункту 7, иначе к пункту 3;
Если условие 3 выполняется, переход осуществляется к пункту 7, иначе к пункту 3;
7) по формулам (18), (19) определяются начальные 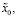
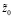 и конечные условия
и конечные условия 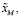
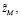
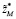 ;
;
8) по формулам (22) и (23) определяются матрицы: 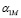 и
и 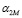 ;
;
9) по формулам (27) определяются матрицы: 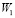 ,
, 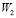 ,
, 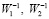 ;
;
10) по формулам (28) и (29) определяются оптимальные управления 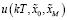 и
и 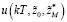 ;
;
11) по формулам (30) и (31) определяются оптимальные траектории 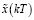 и
и 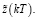
2. Численное моделирование
В этом разделе рассмотрим задачу (1)–(5) для конкретных значений параметров системы (1), где матрицы A и B имеют вид:
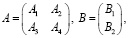
 ,
,



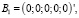
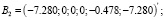 малый параметр –
малый параметр – 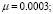
начальные и конечные условия – 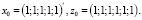
Далее по алгоритму решений задачи (п. 1.3) производятся численные расчеты:
1. Вычисление собственных значений матрицы A4 показывает, что условие 1 выполняется:
(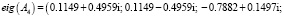
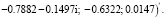
2. Для определения матрицы H и N находим
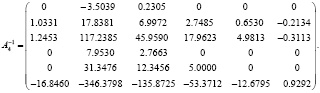
По формулам (14) последовательно вычисляем: H0, H1, … H7 . В результате из (13) при μ = 0.0003 имеем

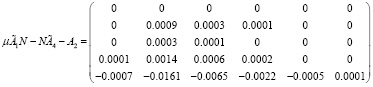
Проверка показала, что матрица H(μ) с точностью O(μ7) удовлетворяет уравнению (11):
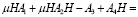

Далее аналогично, по формулам (15) последовательно вычисляем: N0, N1, … N7 и в результате из (13) имеем
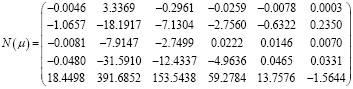
Подставляя N(μ) в (12), убеждаемся, что она удовлетворяет уравнению (12) с точностью O(μ7).
Итак, получаем разделенные переменных состояния системы (8) и (9), где

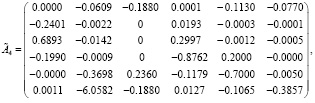
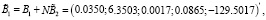
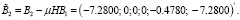
Граничные условия системы (8) и (9) имеют вид
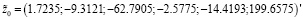 ,
,
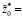 (1.0177e-35; -5.4987e-35; -3.7077e-34; -1.5220e-35; -8.5145e-35; 1.1790e-33)’.
(1.0177e-35; -5.4987e-35; -3.7077e-34; -1.5220e-35; -8.5145e-35; 1.1790e-33)’.
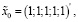
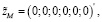
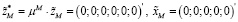 .
.
Согласно пункту 6 проверка условий (3) показывает, что она выполняется:
eig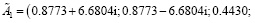
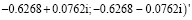
eig 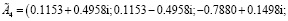
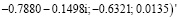 .
.
Согласно пункту 8 по формулам (22) и (23) определяются матрицы: 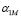 и
и 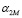 :
:
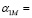 (1.0e+09) *(-0.0111; -0.2371; -0.0694; -0.3620; 6.1360),
(1.0e+09) *(-0.0111; -0.2371; -0.0694; -0.3620; 6.1360),
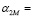 (-0.0990; -0.0394; -0.0633; 0.4662; -0.1671; -0.5998).
(-0.0990; -0.0394; -0.0633; 0.4662; -0.1671; -0.5998).
Согласно пункту 9 по формулам (27) определяются матрицы: 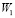 ,
, 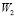 ,
, 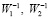 :
:




Результаты численных расчетов задачи (1)–(5) приведены на рис. 1–4.
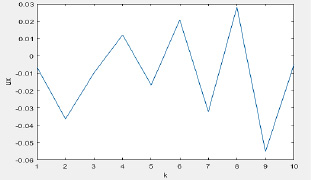
Рис. 1. Результат расчета 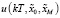 по формуле (28)
по формуле (28)
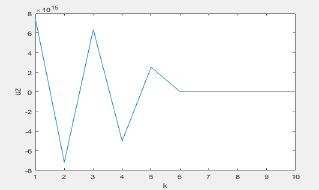
Рис. 2. Результат расчета  по формуле (29)
по формуле (29)
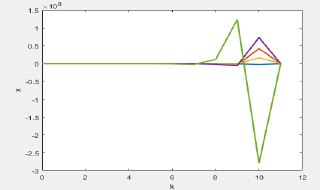
Рис. 3. Результат расчета  по формуле (30)
по формуле (30)
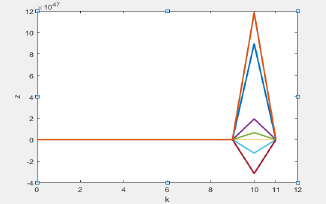
Рис. 4. Результат расчета 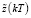 по формуле (31)
по формуле (31)
Заключение
Полученный алгоритм решений линейной сингулярно-возмущенной дискретной задачи оптимального управления с малым шагом на основе разделения переменных состояния системы [13, 14] позволяет существенно понизить порядок исследуемой системы. Полученная при этом эквивалентная система обладает всеми свойствами управляемости и стабилизируемости исходной системы, причем они связаны только управляющей функцией.
Предложенный способ может эффективно применяться при исследовании теории оптимальных цифровых систем управления и при построении приближенного решения алгебраических матричных уравнений Риккати и Ляпунова.

