Scientific journal

International Journal of Applied and fundamental research

ISSN 1996-3955

ИФ РИНЦ = 0,593

Рост вычислительных мощностей для обеспечения требуемого уровня стойкости криптографических систем вызвал необходимость использовать простые числа все большей разрядности. Это привело к необходимости адаптировать трудоемкость вычислительных операций криптографических алгоритмов при нахождении простых чисел [1].

Алгоритмы проверки простых чисел могут быть разделены на две группы: истинные (детерминированные) и вероятностные тесты. Истинные алгоритмы позволяют точно определить простоту числа. Вероятностные тесты позволяют выяснить простое число или нет с определенной вероятностью ошибки [2].

На сегодняшний день существует всего два основных детерминированных алгоритма проверки простого числа, это теорема Вильсона и метод Эратосфена. Метод Эратосфена предполагает простой подбор делителей, что является достаточно сложным из-за большого количества необходимых операций [3]. Проверка простого числа по теореме Вильсона также имеет высокую сложность расчета.

При определении простых чисел высоких порядков в основном используют тест Ферма, который является вероятностным. Благодаря быстрым алгоритмам, основанным на китайской теореме об остатках [4], проверку числа можно осуществить достаточно быстро, но данный тест не позволяет проверить псевдопростые числа Ферма, которые обладают некоторыми свойствами простых чисел, но не являются ими.

Целью данной работы было найти взаимосвязь теста Ферма и теоремы Вильсона, так как нет понимания, почему тест Ферма не распознает псевдопростые числа. На сегодняшний день считается, что эти две теоремы не связаны между собой и имеют совершенно разные принципы расчета. В данной статье представлены результаты исследований, которые наглядно показывают, каким образом тест Ферма соотносится с теоремой Вильсона, что имеет большое значение для дальнейшей адаптации алгоритма поиска и проверки простых чисел.

Теорема Вильсона формулируется следующим образом: Если р простое число, то имеет место сравнение (р – 1)! + 1 ≡ 0 (mod p) (1). Так же справедлива обратная теорема: Если для целого положительного р имеет место соотношение (1), то р число простое, т.е. если сумма (р – 1)! + 1 делится на р без остатка, то число р является простым числом. Проблема заключается в том, что даже при небольших числах n, число (n – 1)! + 1 очень большое число. Например, если по данному алгоритму проверить, является ли число 997 простым, то надо проверить делимость числа 996! + 1 на 997. Данное число содержит 2556 десятичных знаков, что существенно усложняет проверку [5]. Поэтому алгоритм проверки простого числа по теореме Вильсона имеет в основном теоретическое значение и не применяется на практике.

Оптимизация алгоритма по теореме Вильсона заключается в использовании китайской теоремы об остатках. При расчете факториала предположительно простого числа р на каждом этапе находится остаток от деления на р и последующее умножение производится уже этого остатка. Пример расчета числа 97 по данному алгоритму представлен в табл. 1.

Первые четыре числа не отличаются от стандартного расчета факториала. Пятое число больше числа р и равно 120, поэтому берется остаток от деления на 97, что составляет 23. Шестое число находится произведением 23 на 6 и аналогично находится остаток от деления данного числа на 97. Число с порядковым номером 96 действительно равно 96 (или р–1), что является доказательством простого числа р по теореме Вильсона. Таким образом, чтобы определить остаток от деления факториала 97, вычисление самого факториала не требуется. Более того, если последовательно перемножить числа получившегося ряда и аналогично выделять остаток от деления после каждой операции, то в результате найдем остаток от деления суперфакториала проверяемого числа.

Таблица 1

Пример расчета по алгоритму числа 97

Таблица 2

Пример расчета по алгоритму числа 57

Рассмотрим проверку составного числа по данному алгоритму. Выполним расчет по числу 57. Результаты приведены в табл. 2.

Число не прошло проверку, так как после восемнадцатого числа остаток от деления составил ноль. Соответственно, последующее число алгоритм рассчитывает как 0 × 20 = 0. Все последующие числа будут также равны нулю, поэтому условие (р – 1)! + 1 ≡ 0 (mod p) не выполняется.

Метод Эратосфена и теорема Вильсона основаны на разных принципах проверки. В первом случае происходит деление проверяемого числа на возможные множители. Теорема Вильсона основана на том принципе, что если у числа есть делители, то их произведение, умноженное на любое число, будет делить без остатка исходное число. Например, если число 35 делится на 7 и 5, то произведение 7×5×n, при любом целочисленном значении n, будет делиться без остатка на число 35. Минимальный возможный делитель для нечетного числа это 3, поэтому проверку по данному алгоритму необходимо и достаточно выполнить до числа равного р/3. По количеству необходимых операций предложенный вариант уступает методу Эратосфена, где достаточно проверить 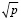чисел [6], однако деление несопоставимых по разряду чисел требует больше времени, чем близких по количеству десятичных знаков.

На данном этапе алгоритм возможно оптимизировать, понимая особенности десятичной системы счисления. Если проверку проходит число, которое оканчивается на три, то оно может быть получено только умножением чисел вида x1 × x3 или x7 × x9. Таким образом при возведении факториала количество чисел возможно сократить.

Особенность данного метода в том, что в процессе возведения факториала есть возможность привести число р к виду p / 2n и результат расчета останется верным. При делении на другие числа алгоритм не работает корректно, что уже говорит о тесной взаимосвязи теоремы Вильсона и чисел вида 2n. В качестве примера приведен расчет числа 97, которое в процессе проверки в произвольном порядке делится на различные 2n. Результаты возведения факториала представлены в табл. 3.

Данный алгоритм основан на китайской теореме об остатках и широко применяется в программировании. Если необходимо узнать остаток от деления от произведения нескольких чисел, то на любом этапе умножения допустимо складывать и отнимать исходное число любое количество раз, и это не влияет на результат. На основании данного правила число n допустимо привести к виду n – р, если необходимо узнать остаток от деления числа р.

Рассмотрим проверку простого числа 5 по теореме Вильсона. Для этого необходимо рассчитать 4!. Расчет представляет собой вид: 1×2×3×4. Используя китайскую теорему об остатках, выражение допустимо привести к виду: 1×2×(3-5)×(4-5) = = 1×2×(-2)×(-1) = -(12)×-(22)=4.

Таблица 3

Пример проверки числа 97 с различными делителями вида 2n

При четном количестве множителей результат положительный, при нечетном – отрицательный. Если результат получается отрицательным, то необходимо брать остаток от деления отрицательного числа, то есть принцип расчета не меняется. Теорема В. Серпинского о критерии простого числа хорошо описывает данное правило [7].

Как было рассмотрено выше, доказательством того, что число простое, является наличие положительного остатка от числа 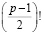Используем китайскую теорему об остатках для записи следующего равенства, на примере числа 5: 1×2 ≡ (-4)×(-3) ≡ 2 (mod 5). Запишем выражение в общем виде:

1×2×…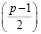 ≡ (1 – р) × (2 – р) ×…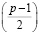– р ≡ n (mod p).

Если число р простое, выполняется следующее условие:

.

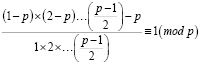Преобразуем выражение в следующий вид:

.

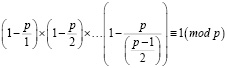Проверим выражение на примере числа 11:

.

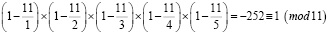Число 11 удовлетворяет условию, значит, данное простое. Эта формула хорошо известна, но имеет свои недостатки [8]. При расчете больших чисел появляется ошибка, вызванная приближенными значениями множителей.

Рассмотрим детально, как выполняется расчет:

.

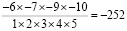Как видно, все числа из знаменателя сокращаются с числителем, умножение производится уже оставшихся значений: -3×-7×-2×-3×-2 = – 252. Дробных чисел при таком расчете получиться не может, так как знаменатель всегда будет сокращаться с числителем.

Чтобы понять закономерность, по которой формируется итоговое число, рассмотрим более высокое простое число, например 23:

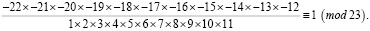
Разобьем выражение на два. Рассмотрим отдельно четные и нечетные числа по знаменателю.

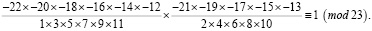
Далее посчитаем результат по первой части:

.

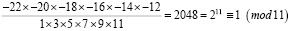Результатом деления получилось число вида 2n. Данный результат не является случайным и имеет закономерность, при p > 8:

.

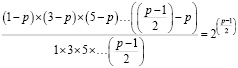В расчете может получиться как положительное, так и отрицательное число. Принцип не меняется: если число отрицательное, то остаток от деления вычисляется от отрицательного числа. Наглядно видна связь данного выражения с малой теоремой Ферма: Если p – простое число, то оно удовлетворяет сравнению ap–1 ≡ (mod p). Как правило, проверка простых чисел ведется именно по основанию 2, так как это наименьшее число. Выведенная формула позволяет оптимизировать выражение до вида

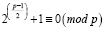, если число p – простое число вида 8k + 3 или 8k + 5.

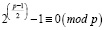, если число p – простое число вида 8k + 1 или 8k + 7.

Разделение проверяемых чисел на две группы обусловлено количеством умножений отрицательных чисел, что наглядно видно из расчета, приведенного выше.

Данное условие является необходимым, но не достаточным признаком простого числа. Для полного доказательства простого числа необходимо решить вторую часть уравнения и доказать, что

.

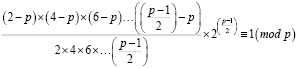Доказательство данной части формулы требует расчета факториала, что затрудняет вычислительный процесс. Адаптация этой части уравнения остается открытым вопросом.

Предложенная формула значительно облегчает доказательство простых чисел, так как сокращает количество необходимых операций при прохождении теста простоты Ферма в два раза. Выведенное выражение раскрывает взаимосвязь малой теоремы Ферма и теоремы Вильсона, что открывает новые возможности изучения простых и псевдопростых чисел Ферма.