В теории дифференциальных уравнений в частных производных исследованы различные прямые и обратные задачи, и для решения этих задач рассмотрены различные методы, связанные с функциями Римана, Грина, с преобразованиями Лапласа, Фурье и др., которые встречаются в работах [1–3] и т.д.
Большое значение в этой области имеют обратные задачи [4–6] и др., где вырождаются нелинейные интегральные уравнения первого или третьего рода с особыми решениями [3], так как их исследования еще не завершены, т.е. не имеют общих методов решения. В некоторых случаях разработаны способы исследований, связанные с методами регуляризации, имеющие сингулярности относительно малого параметра [2].
В связи с этим в настоящей статье изучается многомерная коэффициентная обратная задача с дифференциальным оператором гиперболического типа, вырождающее двумерное интегральное уравнение первого рода с особым решением. Чтобы доказать регуляризируемость исследуемой обратной задачи в введенном пространстве, применяются: метод вспомогательной функции, метод регуляризации операторных уравнений и элементы математического и функционального анализов [7, 8].
Основной целью данного исследования является получение достаточного решения обратной задачи, вырожденной в интегральное уравнение первого рода посредством нахождения соответствующего регуляризирующего решения. Наряду с этим построение алгоритма асимптотического характера, где содержится сингулярная функция относительно малого параметра, также доказательство регуляризируемости в обобщенном смысле и единственности решения исходной задачи во введенном пространстве.
Материалы и методы исследования
В данной работе показаны материалы для важной отрасли высшей математики, такой как теория обратных задач, где применены методы исследования дифференциальных и интегральных-операторных уравнений, методы вспомогательной функции, методы интегрализации, а также методы регуляризации и элементы математического и функционального анализов. Использованы понятия построения регуляризирующего алгоритма получения достаточного решения и оценки их погрешностей.
Результаты исследования и их обсуждение
Пусть задается обратная задача вида
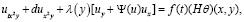 (1)
(1)
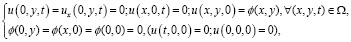 (2)
(2)
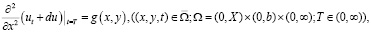 (3)
(3)
где
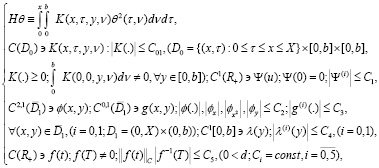 (4)
(4)
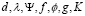 – известные функции. Тогда при указанных условиях требуется найти вектор-функцию:
– известные функции. Тогда при указанных условиях требуется найти вектор-функцию: 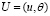 с двумя компонентами из
с двумя компонентами из 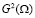 с нормой:
с нормой:
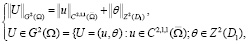
здесь [8]: 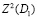 – пространство, элементами которого являются все суммируемые с квадратом функции из
– пространство, элементами которого являются все суммируемые с квадратом функции из 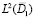 , а также обобщенные функции z(x, y) сосредоточенные в начале координат отрезка [0, X] по переменной х с условием
, а также обобщенные функции z(x, y) сосредоточенные в начале координат отрезка [0, X] по переменной х с условием
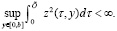
Чтобы исследовать исходную обратную задачу, сперва эту задачу приводим к интегральному виду. С этой целью введем вспомогательную функцию V по правилу:
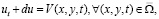 (5)
(5)
где V – новая искомая функция с условиями
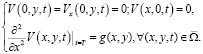 (6)
(6)
Тогда из формулы (5) следует
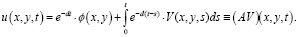 (7)
(7)
Применяя формулы (5), (7) относительно (1) получим
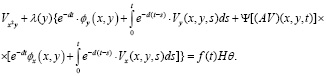 (8)
(8)
Далее, интегрируя (8) по y, имеем
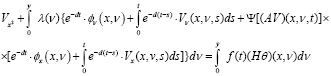
или
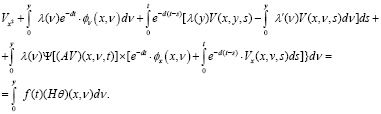 (9)
(9)
Поэтому, допуская
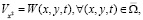 (10)
(10)
с условием
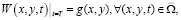 (11)
(11)
получим
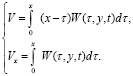 (12)
(12)
Вследствие этого, так как имеет место (10), (12), из (9) следует интегральное уравнение вида
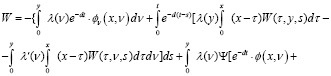 (13)
(13)
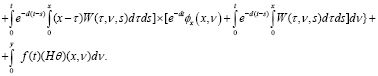
Из (13) видно, что неизвестными являются (W, θ). Значит, на основе (11) из (13) вытекает
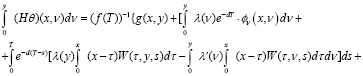 (14)
(14)
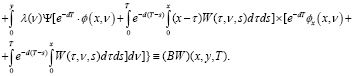
Тогда на основе (13) и (14) получим
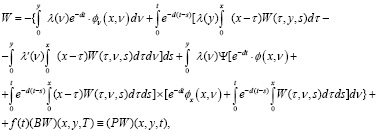 (15)
(15)
где (13) является интегральным уравнением второго рода по переменным x.
Лемма 1. При наложении исходных условий относительно известных функций 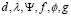 и
и
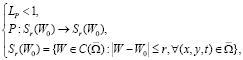 (16)
(16)
уравнение (15) разрешимо в 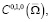 и решение строится по правилу Пикара:
и решение строится по правилу Пикара:
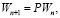
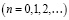 (17)
(17)
с оценкой погрешности
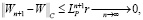 (18)
(18)
где W0 – начальное приближение, а 0 < LP – коэффициент Липщица оператора P. Тогда с учетом (12) и функция V определяется единственным образом в 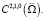 Поэтому на основе (7) и существует единственная функция
Поэтому на основе (7) и существует единственная функция 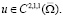
Доказательство. Выше сказано, что (15) является интегральным уравнением второго рода и при условии (16) относительно оператора P реализуются условия Банаха. Поэтому уравнение (15) разрешимо в 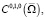 причем решение можно найти по правилу (17). Тогда, на основе выводов этого метода, имеем, что последовательность функций
причем решение можно найти по правилу (17). Тогда, на основе выводов этого метода, имеем, что последовательность функций 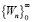 сходится к решению
сходится к решению 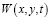 уравнения (15)
уравнения (15) 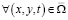 с оценкой (18), где
с оценкой (18), где
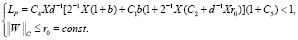
С другой стороны, учитывая (10), (12), получим, что функции  ограничены
ограничены  так как ограничено W,
так как ограничено W, 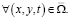 А это означает, что V определена единственным образом в классе
А это означает, что V определена единственным образом в классе 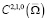 по правилу
по правилу
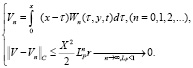 (19)
(19)
Кроме того, так как функция u определяется единственным образом по формуле (7) в 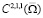 и все частные производные от функции u ограничены
и все частные производные от функции u ограничены 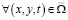 (здесь все частные производные функции u выражаются через функцию V), то имеет место
(здесь все частные производные функции u выражаются через функцию V), то имеет место
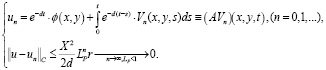 (20)
(20)
Что и требовалось доказать.
Замечание 1. Как выше отмечено, при выполнении условий леммы 1, с учетом (7) функция u однозначно определяется в 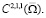 Следовательно, на основе теоремы вложения К. Фридрихса альтернативно можем считать, что функция u единственным образом определяется и в пространстве
Следовательно, на основе теоремы вложения К. Фридрихса альтернативно можем считать, что функция u единственным образом определяется и в пространстве 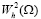 , т.е.:
, т.е.:
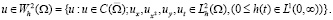
При выполнении условий леммы 1 из соотношения (14), с учетом дифферен-цирования по у, имеем интегральное уравнение первого рода:
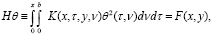 (21)
(21)
где
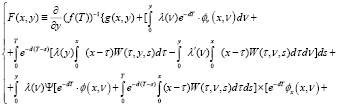 (22)
(22)
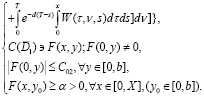
Известно, что при условии (22) интегральное уравнение первого рода (21) некорректно поставленное, т.е. не имеет решения в 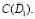 Поэтому, чтобы доказать регуляризируемость (21) в обобщенном смысле, сперва проводим следующие математические преобразования.
Поэтому, чтобы доказать регуляризируемость (21) в обобщенном смысле, сперва проводим следующие математические преобразования.
Если допускаем
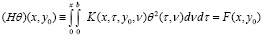 (23)
(23)
и выполнение условий (4), (22), а также
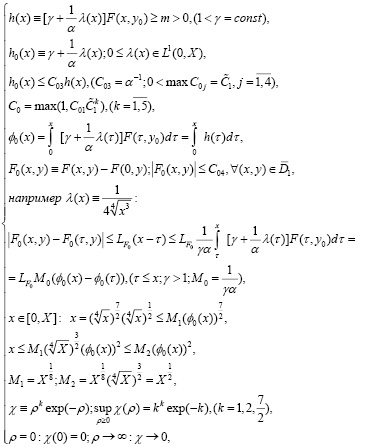 (24)
(24)
то уравнение (21) эквивалентно преобразуется к виду:
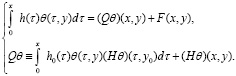 (25)
(25)
Далее, рассмотрим уравнение с малым параметром ε вида
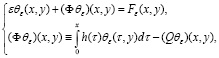 (26)
(26)
с условием
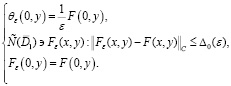 (27)
(27)
При этом решение интегрального уравнения (26) ищем по правилу
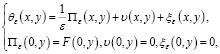 (28)
(28)
причем относительно неизвестных функций имеют место
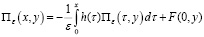 , (29)
, (29)
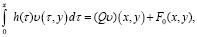 (см. (24)) (30)
(см. (24)) (30)
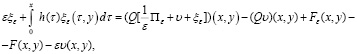 (31)
(31)
где:
а)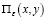 – является решением (29), которое доопределяет особую функцию
– является решением (29), которое доопределяет особую функцию 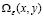 с условием
с условием
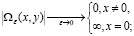 (*)
(*)
б) 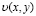 – решение видоизмененного вырожденного уравнения (30), где свободный член в начале отрезка
– решение видоизмененного вырожденного уравнения (30), где свободный член в начале отрезка 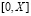 обращается в нуль. При этом функция
обращается в нуль. При этом функция 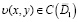 и доказывается, что система (30) регуляризируема в
и доказывается, что система (30) регуляризируема в 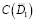 ;
;
в) функция 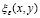 определяется единственным образом из (31), причем сходится к нулю в смысле
определяется единственным образом из (31), причем сходится к нулю в смысле 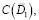 когда малый параметр:
когда малый параметр: 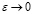 .
.
1. В самом деле, во-первых, из (29) следует
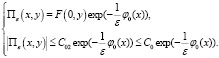 (32)
(32)
Значит, получим (*).
2. Во-вторых, так как функция 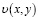 является решением уравнения (30), то, введя уравнение с малым параметром вида
является решением уравнения (30), то, введя уравнение с малым параметром вида
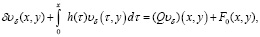 (33)
(33)
можем доказать следующую лемму:
Лемма 2. Если выполняются условия леммы 1 и при этом уравнение (30) имеет решение с условиями (22), (24) и (28), то решение уравнения (33) равномерно сходится к решению (30) при 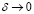 .
.
Доказательство. В условиях леммы 2 уравнение (33) преобразуем к виду
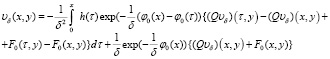 (34)
(34)
и проводим оценки вида
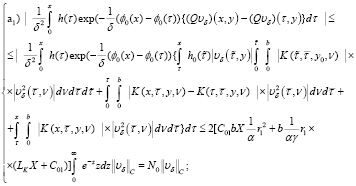
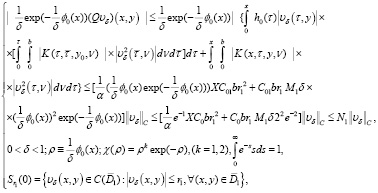
а также
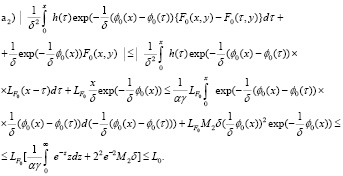
Тогда имеет место
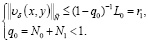 (35)
(35)
С другой стороны, с помощью подстановки: 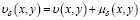 , для любого
, для любого
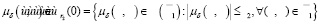 ,
,
получим
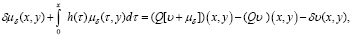
или на основе резольвенты имеем
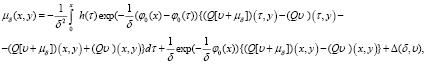
(36)
где
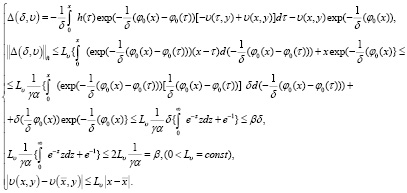 (37)
(37)
Следовательно, учитывая оценки вида
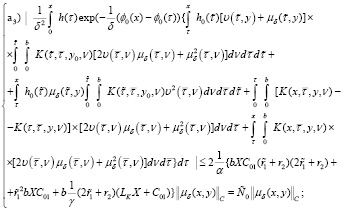
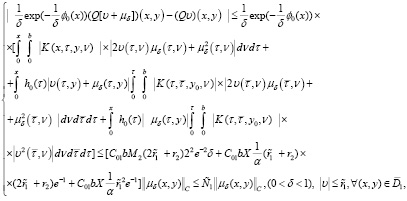
из (36) имеем
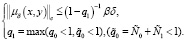 (38)
(38)
А это означает, что
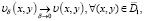 (39)
(39)
т.е. сходится в смысле 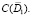 Что и требовалось доказать.
Что и требовалось доказать.
3. Чтобы определить функцию 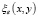 , сперва (31) преобразуем к виду
, сперва (31) преобразуем к виду
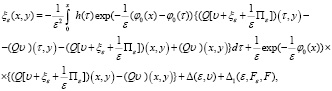 (40)
(40)
где
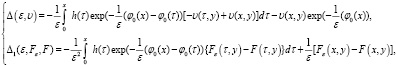 (41)
(41)
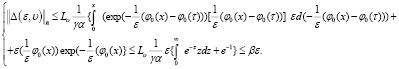
(см (37)).
Далее, для оценки (40) учитываем

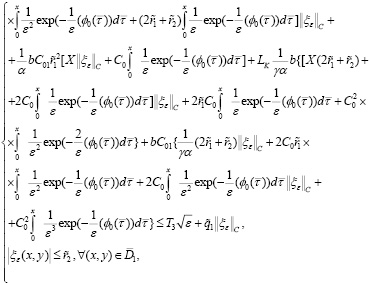
и
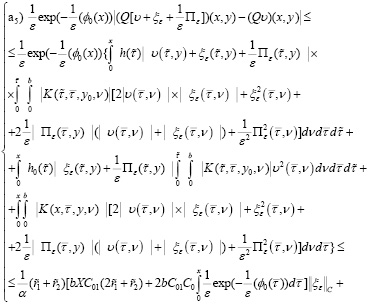
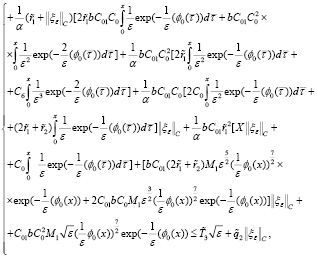
здесь учтены
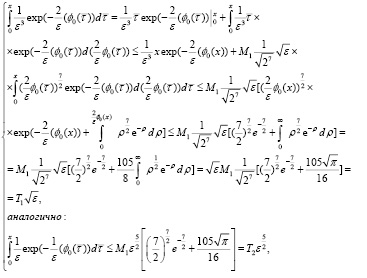
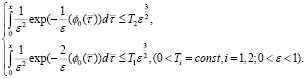
Поэтому из оценки (40) следует
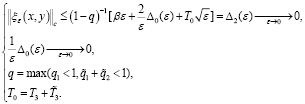 (42)
(42)
Лемма 3. При условиях леммы 1 и (24), (27), (32), (41), (42) уравнение (31) разрешимо в 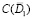 , причем при ε→0 сходится к нулю в смысле
, причем при ε→0 сходится к нулю в смысле 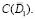
Заключение
А) Если выполняются условия лемм 1–3, то решение уравнения (26) единственным образом представимо в виде (28), при этом***  решение уравнения (26) сходится (неравномерная сходимость) при ε→0 к решению уравнения (30) с оценкой:
решение уравнения (26) сходится (неравномерная сходимость) при ε→0 к решению уравнения (30) с оценкой:
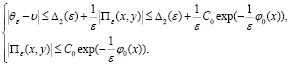 (43)
(43)
Б) А в случае: 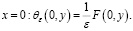
Кроме того, имеет место (*). Поэтому, учитывая вышеуказанные дефекты, пока не можем сказать о близости решений уравнений (26) и (30) в определенном смысле.
Чтобы полноценно оценить близости решений уравнений (26), (30) в этом пространстве, докажем теорему.
Теорема 1. Пусть имеют место условия лемм 1–3 и имеет место (43). Тогда следуют
1) 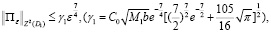 (44)
(44)
2) 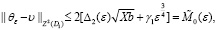 (45)
(45)
3) 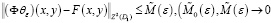 при
при 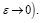
Доказательство. Рассматривая второе соотношение формулы (43) в смысле нормы пространства 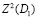 , получим
, получим
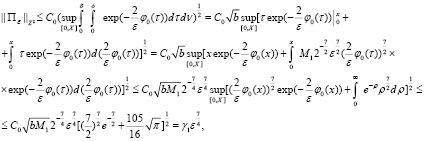
т.е. действительно имеет место (44).
Кроме того, из первого соотношения формулы (43) на основе нормы 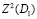 и неравенства
и неравенства 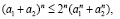
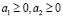 следует
следует
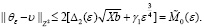
А это означает, что и выполняется неравенство (45).
С другой стороны, с учетом (см. (26))
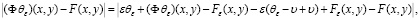
получим
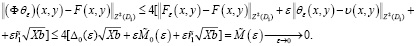
Что и требовалось доказать.
Теорема 2. В условиях леммы 1 и теоремы 2 задача (1)–(3) регуляризируема в 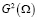 в обобщенном смысле.
в обобщенном смысле.
Заключение
В данной работе рассмотрена многомерная коэффициентная обратная задача с оператором гиперболического типа, вырождающаяся в двумерное интегральное уравнение первого рода с особым решением в G2(Ω). Данная задача исследована с помощью метода вспомогательной функции и метода регуляризации, которые позволили выявить достаточные условия разрешимости этих задач и регуляризируемости в G2(Ω) в обобщенном смысле. Результаты работы могут быть использованы и в других задачах математической физики, где вырождаются нелинейные некорректные интегральные уравнения первого рода.

