Состояние современной гидромеханики в значительной мере характеризуется работами, нашедшими отражение в изданиях [1–3]. Часть данной научной области составлена исследованиями динамики гидромеханических систем при периодических по времени (колебательных, вибрационных) воздействиях, не имеющих выделенного направления в пространстве [4, 5]. В настоящей работе рассматривается новая задача о движении гидромеханической системы при воздействиях, не имеющих выделенного направления в пространстве. Система состоит из идеальной несжимаемой не ограниченной извне жидкости и находящегося в ней твердого тела Ξ (включения, шара) радиуса A. В начальный момент времени t, при t = 0 жидкость и тело Ξ покоятся относительно инерциальной прямоугольной системы координат X, Y, Z. В последующие моменты времени при t > 0 на гидромеханическую систему оказываются воздействия, наличие которых проявляется в том, что скорость жидкости на бесконечности V∞ = {V∞, 0, 0} и радиус включения периодически соответственно с периодами T и τ изменяются со временем. Центр инерции включения совпадает с центром включения. Течение жидкости является потенциальным [6]. Периоды T, τ могут совпадать друг с другом или быть различными.
Целью работы является определение движения гидромеханической системы (жидкости и включения).
Постановка и решение задачи
Пусть S – радиус-вектор центра тела Ξ (центра инерции тела Ξ); Φ – потенциал скорости жидкости; m – масса тела Ξ; ρ – плотность жидкости; Г – граница тела Ξ (сфера радиуса А с центром в центре тела Ξ); n – единичный вектор внешней нормали к Γ; P – давление в жидкости; I – функция t;
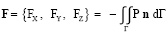 ,
,
– сила, действующая со стороны жидкости на тело Ξ.
Уравнение движения тела Ξ (центра инерции тела Ξ), уравнение неразрывности, интеграл Коши–Лагранжа, граничные и начальные условия имеют следующий вид:
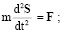 (1)
(1)
ΔФ = 0; (2)
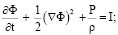 (3)
(3)
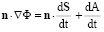 на Г; (4)
на Г; (4)
∇Ф →V∞ при X2 + Y2 + Z2 → ∞ (5)
Ф = 0, S = 0, dS / dt = 0 при t = 0 (6)
(функции A = A(t), V∞ = V∞(t) являются заданными; A = Â, dA / dt = 0, V∞ = 0 при t = 0 (Â > 0 – постоянная)).
Предположим, что
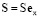 для t > 0 (7)
для t > 0 (7)
то есть при всех t > 0 центр тела Ξ находится на оси X (S = 0, dS / dt = 0 при t = 0). Отметим, что для выполнения (7) необходимо и достаточно, чтобы были удовлетворены условия
FY = 0, FZ = 0 для t > 0. (8)
Зафиксируем (произвольный) момент времени t > 0. Введем в рассмотрение прямоугольную систему координат X1, X2, X3, неподвижную относительно системы X, Y, Z, такую что начало координат X1, X2, X3 совпадает с центром тела Ξ , ось X1 лежит на оси X, и направления осей X2, X3 совпадают соответственно с направлениями осей Y, Z. Будем использовать сферические координаты R, θ, φ, связанные с координатами X1, X2, X3 соотношениями
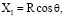
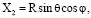
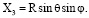
Преобразуем задачу (2), (4), (5) к виду
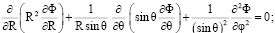 (9)
(9)
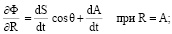 (10)
(10)
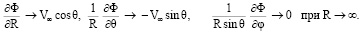 (11)
(11)
Задача (9)–(11) имеет решение
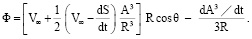 (12)
(12)
Отметим, что согласно (3), (12)
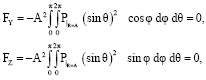
то есть условия (8) являются выполненными.
Используя (1), (3), (6), (12), получим
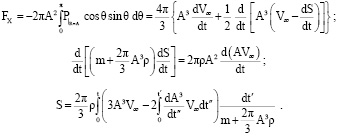 (13)
(13)
Формулами (3), (12), (13) определяется точное решение задачи (1)–(6).
Пусть
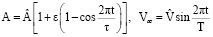 (14)
(14)
(ε ≥ 0 – параметр; 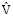 – постоянная).
– постоянная).
Отметим, что согласно (14)
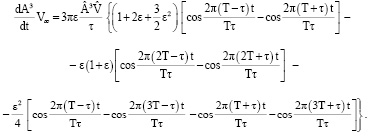 (14)
(14)
Остановимся на вопросе о движении тела Ξ (центра тела Ξ) при малых по сравнению с единицей значениях ε.
Пусть
τ = T. (15)
Используя (12)–(15), получим
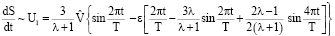 , при ε → 0, (16)
, при ε → 0, (16)
где
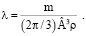
Согласно (16) тело Ξ на фоне колебаний совершает однонаправленное движение со скоростью
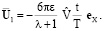 (17)
(17)
Пусть
τ ≠ T. (18)
Подчиним периоды τ, T условию
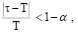 (19)
(19)
где 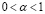 – постоянная.
– постоянная.
Используя (13), (14), (18), (19), получим
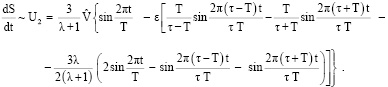 (20)
(20)
Согласно (20) тело Ξ совершает колебания. В частности, при периодах τ, T, близких друг к другу, тело Ξ на фоне «быстрых» колебаний совершает «медленные» колебания со скоростью
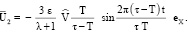 (21)
(21)
Амплитуда «медленных» колебаний тела Ξ (центра тела Ξ) составляет
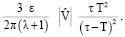 (22)
(22)
Отметим, что согласно (16), (20) предел U2 при стремлении к нулю τ – T равен U1.
Заключение
Проведенное рассмотрение позволило обнаружить, что монопериодические и немонопериодические воздействия на гидромеханическую систему, не имеющие выделенного направления в пространстве, могут приводить к качественно различной динамике системы ((16), (17), (20)–(22)). В частности, в настоящей работе найдено, что при монопериодических воздействиях включение в жидкости на фоне колебаний совершает однонаправленное движение; при немонопериодических воздействиях с близкими периодами включение в жидкости на фоне «быстрых» колебаний совершает «медленные» колебания вдоль прямой линии с периодом, обратно пропорциональным разности периодов, и амплитудой, обратно пропорциональной квадрату разности периодов происходящих в гидромеханической системе заданных периодических изменений – колебаний скорости жидкости на бесконечности и радиуса включения.

