Исследования динамики гидромеханических систем представлены, в частности, в изданиях [1–3]. Экспериментальному и теоретическому изучению влияния периодических по времени (колебательных, вибрационных) воздействий на динамику гидромеханической системы посвящены работы [4, 5].
В [6] поставлена и решена задача о движении гидромеханической системы с вязкой жидкостью, все части которой являются свободными.
Предметом изучения в настоящей работе является следующая задача. Имеется гидромеханическая система, движение которой подлежит определению. Система состоит из абсолютно твердого тела Ξ и вязкой несжимаемой жидкости. Тело Ξ ограничено двумя сферами радиусов A и A′ (A′ > A) с центрами в точке O – начале инерциальной прямоугольной системы координат X, Y, Z. Масса m тела Ξ распределена сферически-симметрично относительно точки O. Разность A′ – A пренебрежимо мала по сравнению с радиусом A, в связи с чем тело Ξ рассматривается как материальная поверхность (сфера массы m, радиуса A, с центром в точке O). Жидкость заполняет область Q: 0 ≤ X2 + Y2 + Z2 < A2. На тело Ξ, наряду с силами со стороны жидкости, действуют внешние силы. Момент Mext внешних сил относительно оси X периодически с периодом T изменяется со временем t. Тело Ξ совершает обусловленные наличием момента Mext вынужденные вращательные колебания вокруг оси X (монотонное вращение тела Ξ вокруг оси X отсутствует).
Целью работы является определение не зависящего от начальных данных движения гидромеханической системы (тела Ξ и жидкости).
Постановка и решение задачи
Пусть τ = t / T, x = X / A, y = Y / A, z = Z / A,
r, θ, φ – сферическая система координат, связанная с системой X, Y, Z соотношениями
x = r cos θ, y = r sin θ cos φ, z = r sin θ sin φ;
er , eθ , eφ – единичные базисные векторы системы r, θ, φ (er = {x / r, y / r, z / r}); V = (A / T) v, υ и ρ – скорость, кинематический коэффициент вязкости и плотность жидкости 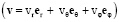 ; P = (ρA2 / T2)p – давление в жидкости; m – масса тела Ξ; I = (2/3)mA2 – момент инерции тела Ξ относительно оси X; Ω = ω / T – угловая скорость вращения тела Ξ вокруг оси X; Re = A2 / (υT) – число Рейнольдса; f = sin2πτ;
; P = (ρA2 / T2)p – давление в жидкости; m – масса тела Ξ; I = (2/3)mA2 – момент инерции тела Ξ относительно оси X; Ω = ω / T – угловая скорость вращения тела Ξ вокруг оси X; Re = A2 / (υT) – число Рейнольдса; f = sin2πτ; 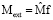 – момент внешних сил, действующих на тело Ξ, относительно оси X (
– момент внешних сил, действующих на тело Ξ, относительно оси X (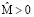 – постоянная);
– постоянная);
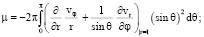
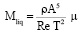
– момент сил, действующих на тело Ξ со стороны жидкости, относительно оси X; 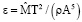 ;
; 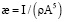 .
.
Уравнение движения тела Ξ, уравнение Навье – Стокса, уравнение неразрывности и условия на твердой границе жидкости имеют вид
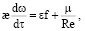 (1)
(1)
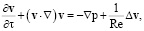 (2)
(2)
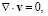 (3)
(3)
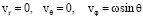 при r = 1. (4)
при r = 1. (4)
Будем рассматривать задачу (1)–(4) при малых по сравнению с единицей значениях ε. Применим метод разложения по степеням малого параметра. Предположим, что
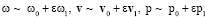
при ε → 0. (5)
Используя (1)–(5) в εN – приближении (N = 0, 1), получим
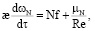 (6)
(6)
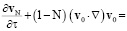
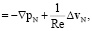 (7)
(7)
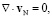 (8)
(8)
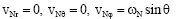
при r = 1, (9)
где
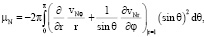
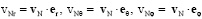 .
.
Пусть N = 0. Задача (6)–(9) имеет решение
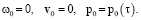 (10)
(10)
Пусть N = 1. Будем искать решение задачи (6)–(9), имеющее вид
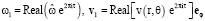
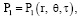 (11)
(11)
где 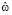 – постоянная. Отметим, что для (11) уравнение (8) является выполненным. Используя (6), (7), (9), (11), найдем
– постоянная. Отметим, что для (11) уравнение (8) является выполненным. Используя (6), (7), (9), (11), найдем
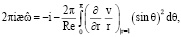 (12)
(12)
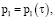 (13)
(13)
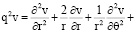
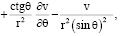 (14)
(14)
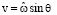 при r = 1, (15)
при r = 1, (15)
где 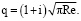 Сделаем в (14), (15) подстановку
Сделаем в (14), (15) подстановку
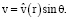 (16)
(16)
В результате этого получим
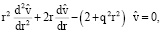 (17)
(17)
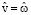 при r = 1. (18)
при r = 1. (18)
Задача (17), (18) имеет решение
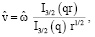 (19)
(19)
где I3/2 – модифицированная функция Бесселя.
Отметим, что ввиду наличия соотношения
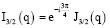
(J3/2 – функция Бесселя), согласно теореме Ломмеля
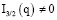
для любого положительного значения Re. Из (11), (15), (16), (19) следует
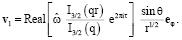 (20)
(20)
Используя (12), (16), (19), получим
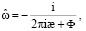 (21)
(21)
где 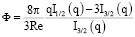
(I1/2 – модифицированная функция Бесселя).
Формулами
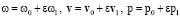 (22)
(22)
и (10), (11), (13), (20), (21) определяется приближенное решение задачи (1)–(4).
Остановимся на вопросе о движении тела Ξ при малых и больших (по сравнению с единицей) значениях числа Рейнольдса.
Предварительно отметим следующее.
1. Пусть область Q заполнена не жидкостью, а однородным твердым телом Ξ′ (шаром радиуса A с центром в точке O) плотностью ρ, и тела Ξ, Ξ′ колеблются как одно твердое тело. Тогда движение системы (тела Ξ и тела Ξ′) определяется уравнением
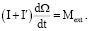 (23)
(23)
Здесь 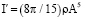 – момент инерции тела Ξ′ относительно оси X. Из (23) следует
– момент инерции тела Ξ′ относительно оси X. Из (23) следует
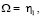 (24)
(24)
где
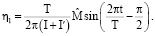
2. Пусть в области Q отсутствует какая-либо материальная среда. Тогда движение системы (тела Ξ) определяется уравнением
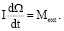 (25)
(25)
Из (25) следует
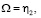 (26)
(26)
где
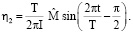
Отметим, что «твердотельные» колебания η1 , η2 имеют сдвиг по времени на – T/4 по отношению к моменту Mext.
Обратимся к полученному решению задачи (1)–(4). Используя (10), (11), (21), (22), найдем
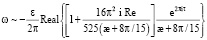
при Re → 0, (27)
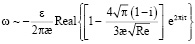 при Re → ∞. (28)
при Re → ∞. (28)
Из (27), (28) следуют приближенные формулы
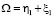 (29)
(29)
– для малых значений Re; здесь
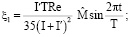 (30)
(30)
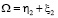 (31)
(31)
– для больших значений Re; здесь
 (32)
(32)
Согласно (29), (31) и при малых, и при больших значениях Re угловая скорость Ω представляет собой сумму «больших» колебаний (которые совпадают с «твердотельными» колебаниями (24), (26)) и «малых» колебаний (30), (32). Отметим, что при малых значениях Re «малые» колебания угловой скорости имеют нулевой сдвиг по времени; при больших значениях Re «малые» колебания угловой скорости имеют сдвиг по времени –7T / 8 по отношению к моменту Mext .
Заключение
В настоящей работе определено движение гидромеханической системы с вязкой жидкостью. Тем самым установлено, каковы отклики системы на оказываемые на нее периодические по времени воздействия. Найдено, в частности, что при малых и больших (по сравнению с единицей) значениях числа Рейнольдса присутствие в системе вязкой жидкости проявляется в наличии «малых» колебаний угловой скорости окружающего жидкость твердого тела. Формулами (30), (32) демонстрируется связь между параметрами гидромеханической системы и являющимися наблюдаемыми «малыми» колебаниями угловой скорости вращения твердого тела.
Полученные результаты могут использоваться, в частности, в исследованиях возможностей малоинвазивного изучения строения гидромеханических систем.

