Предметом начертательной геометрии (GEOMETRIE DESCRIPTIVE), созданной Гаспаром Монжем [1], является способ построения проекций геометрических тел и их поверхностей, а также точек, линий, плоскостей, эллипсов, гипербол и др.
Учение Г. Монжа положено в основу современной графической инженерной подготовки и используется при создании конструкторской документации при проектировании любых конструкций и сооружений. Система ЕСКД (единая система конструкторской документации) базируется на теории ортогонального проецирования, теоретические основы которого содержит начертательная геометрия. Например, ГОСТ 2.305-2008 «Изображения. Виды, разрезы, сечения».
Однако, что менее известно, Г. Монж в своем основополагающем труде «Начертательная геометрия» [1] уделяет значительное место «применению пересечений к решению различных задач», то есть задач смежных дисциплин, которые изучаются в высшей школе.
Развитие этих методов наиболее полно представлено в сборнике задач Н.Ф. Траутман [2], где приведены графические способы решения задач из различных научно-технических областей: физики, механики, материаловедения и др.
Методы решения практических задач, приведенные в учебнике, не нашли широкого применения по объективной причине. Это недостаточная точность вычислений по объектам, которые построены при помощи чертежных инструментов: линейки, циркуля и карандаша.
Графические редакторы с их мощным математическим ядром меняют ситуацию. Только за счет точного построения прямых и циркульных линий, а также измерения координат точек, углов, длин отрезков и площадей можно получить не только математически точные численные ответы, но качественно новые научные результаты [3].
В математике широко используется визуализация уравнений в виде графиков функций. Но возможность сдвига их на чертеже методами НГ позволила доказать, что число корней уравнений зависит только от численной величины свободного члена [4].
Визуализация математического аппарата с «парой чисел» позволила создать теорию графического вычисления на обычной плоскости [5].
В международной системе единиц СИ [6, с. 25] указано, что единица измерения телесного угла не имеет размерности. Однако авторский метод двухкоординатной равновеликой развертки позволяет предложить и размерность, и способ ее количественного измерения.
Созданный в развитие теории начертательной геометрии авторский метод проекций с временными отметками позволил количественно решать пространственно-временные задачи с семью и более переменных [7].
Манипуляции с графиками функций не только позволили создать графическую теорию мнимых чисел, которая подтверждена сечениями геометрических тел (конусов вращения), но и предложить общие математические зависимости описания некоторых «замечательных» кривых; эллипса, гиперболы и окружности [8].
Изложенные результаты графических исследований позволили обобщить их термином «вычислительная графика». В развитие теории начертательной геометрии предлагаем метод, позволяющий решать задачи по определению величин, характеризующих физические процессы.
Материалы и методы исследования
Рассмотрим примеры классических задач.
Задача 1. В бассейн проведены 5 труб: A, B, C, D, E. Через некоторые из них вода вливается, через другие – выливается. Известно, что при совместном действии труб В, С, Е бассейн заполняется за 6,94 ч (m), труб А, С, D – за 5,17 ч (n), труб А, Е – за 11,68 ч (р), а труб В, D – 14,66 ч (g). За какое время заполнится бассейн одной трубой С?
Графическое решение задачи показано на рис. 1. На нем в координатах время (ось абсцисс в масштабе) – объем бассейна (ось ординат) показано его заполнение заданными комбинациями труб в отдельности (m, n, p, g). Особенность метода в том, что цифровые значения используются только при вводе исходных данных и получении ответа.
Графическое сложение. Ординаты (отрезки) часовой (допустима любая) производительности комбинаций на прямой добавляются друг к другу. Результат (2,49) – время заполнения бассейна двойным набором труб, так как они упоминаются в условии дважды (каждая).
Графическое умножение. Построение симметричного относительно вертикальной оси симметричного отрезка. Результат – время заполнения бассейна одним комплектом труб (4,98).
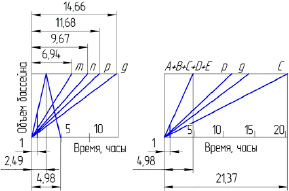
Рис. 1. Графическое решение задачи наполнения бассейна
Графическое вычитание. Из суммарной производительности вычитается производительность комбинаций p и g, так как в них не упоминается труба С.
По полученной разности строится график работы искомой трубы, и измерением абсциссы определяется искомое время: 21,37.
Для сравнения ниже показан математический расчет времени заполнения бассейна одним комплектом:
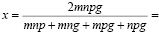
 .
.
Логичность графических построений покажем и на следующем примере, решения задачи на определение взаимного положений и скорости двух движущихся тел.
Задача 2. Два тела, с постоянной скоростью навстречу друг другу, столкнутся через m с. Если же одно тело будет догонять другое, то столкновение произойдет через n с при тех же скоростях. Определить скорости обоих тел, расстояние, пройденное быстрым телом, если известно, что первоначально тела находились на расстоянии d друг от друга. Пусть дано: m = 15,69; n = 35,52; d = 40 произвольных единиц.
Решение выполним на графике в координатах время/расстояние (рис. 2). На оси абсцисс отметим в масштабе заданные значения m и n, а скорость быстрого тела изобразим произвольной наклонной линией, выходящей из начала отсчета. На графике скорости отметим точки а и b: точки встречи двух тел, двигающихся навстречу (а) и вдогонку (b).
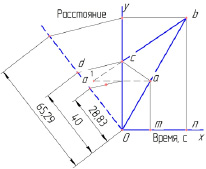
Рис. 2. Графическое решение задачи движения двух тел
Скорость медленного тела строго соотносится со скоростью быстрого и поэтому произвольно на графике построена быть не может. Но, по условию задачи, известно, что ее скорость постоянна. Следовательно, угол наклона ее графика к оси ординат в неизвестной точки с должен быть одинаковым (вверх и вниз). Эта задача характерна для оптики, биллиарда, определения расстояния до Луны (двойное отражение). В данном случае достаточно построить точку a´, симметричную а относительно оси ординат.
Определение искомых расстояний осуществим методом подобия по известному параметру d.
Скорости тел, вычисленные аналитически, составляют 0,71 и 1,84. Однако в графической программе их также можно вычислить методом подобия (рис. 2).
Методы начертательной геометрии применимы для решения задач теоретической механики, определения характерных точек движущегося звена, например, мгновенного центра скоростей.
Задача 3. Графически найти положение мгновенного центра при перемещении звена АВ. Вычислить углы поворота относительно центра точек А, В и звена АВ в целом.
Мгновенный центр всегда находится в точке пересечения двух перпендикуляров, проведенных через середины отрезков, отображающих путь перемещения точек А и В. Измерения показали, что углы перемещения точек А и В численно равны и составляют 33º15´.
Более того, в результате графического анализа установлено, что отрезок АВ, перемещаясь на величину 30 м, одновременно поворачивается на точно такой же угол (рис. 3).
Отметим, что расширительно начертательная геометрия позволяет найти мгновенную ось произвольного перемещения звена АВ в пространстве (в пространстве это может быть только ось). Приведем алгоритм ее нахождения.
Построить две параллельные плоскости, в которых перемещаются точки А и В.
Двукратной заменой плоскостей проекций (метод начертательной геометрии) найти истинную величину перемещений в соответствующих плоскостях точек А и В (АА1 и ВВ1).
Построением перпендикуляров через середину к отрезкам АА1 и ВВ1 в каждой плоскости найти точку, принадлежащую мгновенной оси.
Обратным построением найти проекции положения мгновенной оси в пространстве.
Для сведения отметим, что два положения звена в пространстве являются двумя образующими гиперболоида.
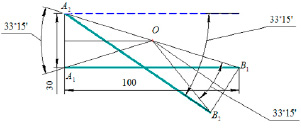
Рис. 3. Численное графическое определение мгновенного центра
Скорее всего, только методы начертательной геометрии позволят решать задачи теоретической механики, так как в этой учебной дисциплине вторые проекции объектов обычно не используются.
Методами начертательной геометрии можно, дополнительно или взамен, исследуя движение точки, вычислять ее скорость, нормальное и касательное ускорения, параметры кривизны и др.
Выводы
В результате нашего исследования можно заключить, что:
− Дисциплина «Начертательная геометрия» закладывает основы ортогонального проецирования – теории построения чертежа. Чертеж – это документ, содержащий изображение изделия и другие данные, необходимые для изготовления изделия. Построение изображений изделий – это необходимая техническая компетенция, которую осваивает будущий инженер.
− Методы начертательной геометрии применимы для решения задач смежных дисциплин, нахождения физических параметром объектов трехмерного пространства, характеристики физических процессов, определение параметров, характеризующих движение точки и твердого тела. Здесь значение имеет точность построений, недостижимая при построении чертежа ручными методами: линейка, карандаш, циркуль.
− Использование для графических построений компьютерных программ [9], обладающих математическим ядром и отличающихся высокой (до восьми знаков после запятой) точностью построений позволяет применить методы начертательной геометрии в практических ситуациях, для решения технических и физических задач, что и продемонстрировано в данной публикации.
− Графические способы решения задач общетехнических дисциплин позволяют находить различные физические величины, характеризующие процессы, происходящие в материальном мире, как изменение объема, так и скоростные характеристики движущейся точки, движущегося звена, найти характерные точки движущихся объектов и определить их положение в пространстве в заданной системе отсчета, что невозможно при решении задач аналитическими методами.

