Scientific journal

International Journal of Applied and fundamental research

ISSN 1996-3955

ИФ РИНЦ = 0,593

Выведение спутников на низкую околоземную орбиту возможно как с применением вертикального, так и с горизонтального старта, когда ракета-носитель выводится на некоторую высоту с дозвуковой скоростью самолетом, после чего происходит ее сброс и включение двигателей первой ступени. Горизонтальный старт имеет ряд преимуществ, особенно в классе легких ракет, выводящих небольшие по массе грузы на невысокие орбиты Земли. Примером таких ракет может служить американская ракета «Пегас» [1]. Она имеет 3 ступени с двигателями, работающими на твердом топливе. Относительная масса топлива составляет для нее около 90 % от стартовой массы. Представляет интерес оценить возможность вывода на низкую околоземную орбиту одноступенчатой ракеты с горизонтального старта, которая будет оборудована двигателем с изменяемым вектором тяги. Проведенный численный эксперимент в данной работе представляет собой предварительную оценку такой возможности с рядом допущений и упрощений математической модели. Задача оптимизации управления вектором тяги была решена методом пристрелки с использованием принципа максимума Понтрягина. Расчет аэродинамического сопротивления проводился при допущении постоянства коэффициента аэродинамического сопротивления 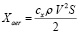, где сx – коэффициент аэродинамического сопротивления, ρ – плотность воздуха, зависящая от высоты, V – скорость полета, S – характерная площадь летательного аппарата (в данной задаче площадь миделя ракеты). Это связано с тем, что достижение сверхзвуковых скоростей на высотах выше 12000 м происходит достаточно быстро, а основное изменение коэффициента аэродинамического коэффициента происходит на трансзвуковых скоростях [2]. Также предполагалось, что ракета имеет аэродинамические рули, позволяющие поддерживать нулевой угол атаки и не создающие значительной подъемной силы. Кроме этого, не рассматривались ограничения на возможный угол отклонения вектора тяги и прочностные ограничения конструкции ракеты. Плотность воздуха аппроксимировалась экспоненциальной зависимостью, дающей достаточно хорошее совпадение со значениями Международной Стандартной Атмосферы [3] на высотах от 13 км и выше.

Цель исследования – провести численный эксперимент для легкой ракеты горизонтального старта, идентичной по параметрам первой ступени ракеты «Пегас», решить задачу оптимизации управления (угол действия тяги двигателя), используя принцип максимума Понтрягина методом пристрелки, по полученным результатам оценить возможность вывода на низкую орбиту Земли одноступенчатого варианта ракеты.

Математические модели и численные методы

Критерий эффективности управления – минимум затрат топлива на выполнение миссии или минимум времени вывода ракеты на орбиту при постоянном уровне тяги, а следовательно, и расхода топлива.

.

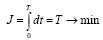Система уравнений движения в полярной системе координат:

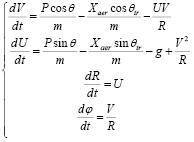
где R – расстояние от центра Земли, м; V – скорость, перпендикулярная радиусу, м/с; U – скорость вдоль радиуса, м/с; φ – угол, рад; P = JGT – тяга двигателя, Н; J – импульс ракетного двигателя, м/с; GT – расход топлива, кг/с; Xaer – сила аэродинамического сопротивления, Н; m– масса ракеты, кг; 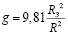– ускорение свободного падения, м/с2, RЗ – радиус Земли, м; t – время, с, θ – управление, угол действия тяги (между осью ракеты и направлением силы тяги), рад, θtr – траекторный угол (между скоростью и перпендикуляром к местному радиусу), рад,

; ;

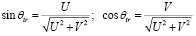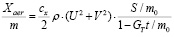ρ = 1,703746625(R – RЗ)exp(–0,000142422) – плотность воздуха по высоте, кг/м3, S / m0 – относительная площадь миделя ракеты.

В качестве исходных данных были приняты технические характеристики первой ступени ракеты Пегас. Момент сброса ракеты с самолета-носителя принимался при высоте 13000 м и горизонтальной скорости полета при М = 0,85. При использовании принципа максимума Понтрягина функция Понтрягина имеет вид

,

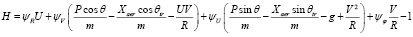где ψR, ψV, ψU, ψφ, – сопряженные переменные.

Максимум функции Понтрягина по управлению определим из .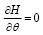

Отсюда для оптимального управления

.

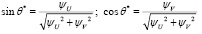Дополним систему уравнений движения сопряженной системой:

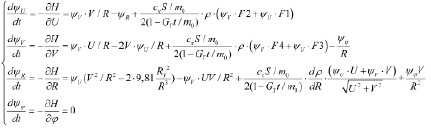
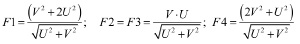
Получим П-систему с краевыми условиями:

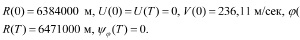
Решение было получено методом пристрелки. Метод пристрелки или стрельбы дает наиболее точные результаты численного решения краевых задач [4]. Возможность решения реальных задач оптимального управления указанным методом как для задач без ограничений по управлению, так и для задач с переключением управления показана в [5–7]. Внешний цикл – модифицированный метод Ньютона обращается к численному методу решения задачи Коши – методу Рунге – Кутты 4-го порядка. Для более точного выхода из метода численного интегрирования вводился новый аргумент 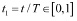, где Т – время вывода ракеты на орбиту соответственно, П-система претерпевает изменения, связанные с ведением нового аргумента.

Параметры пристрелки и невязки для этого варианта расчета выбирались следующие:

ψr(0), ψV(0), ψU(0), T, – параметры пристрелки

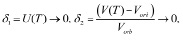
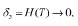
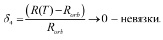
Точность вычислений определялась условием: max{|δi|}<10–5 (i ∈ [1, 4]).

Результаты расчетов

Расчеты были проведены для различных значений удельного импульса топлива (2000 м/с и 4000 м/с) и для дозвуковой скорости старта и небольшой сверхзвуковой скорости старта ракеты (соответствующим на 13 км числу Маха полета М = 0,85 и М = 2).

Результаты расчетов приведены на рис. 1–6 и в таблице. Варианты 1 и 3 расчета соответствовали дозвуковой скорости старта и удельным импульсам топлива, равным соответственно 2000 м/с и 4000 м/с. Варианты 2 и 4 соответствовали сверхзвуковой скорости старта и удельным импульсам топлива, равным соответственно 2000 м/с и 4000 м/с.

Заключение

Увеличение начальной стартовой скорости с дозвуковой до сверхзвуковой при М = 2 оказывает незначительное влияние на время вывода ракеты на орбиту, а следовательно, почти не снижает потребные затраты топлива. Вместе с тем переход через трансзвуковые скорости значительно увеличивает нагрузку на начальный носитель ракеты и усложняет конструктивное решение.

Увеличение значения импульса ЖРД сокращает потребное количество топлива почти на 20 %, что делает реализацию одноступенчатой ракеты-носителя с горизонтальным стартом при оптимальном управлении вектором тяги вполне вероятной.

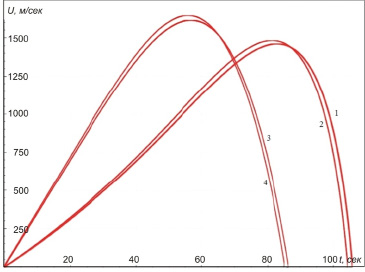
Рис. 1. Изменение радиальной скорости ракеты по времени при выводе ее на низкую орбиту Земли

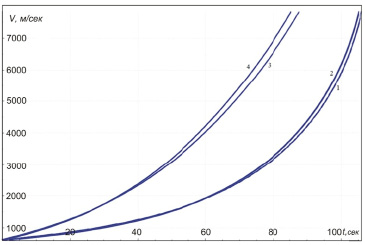
Рис. 2. Изменение окружной скорости ракеты при выводе ее на низкую орбиту Земли

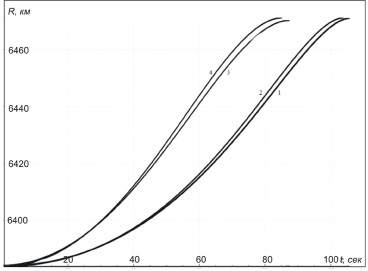
Рис. 3. Изменение радиуса (расстояния от центра Земли) при выводе ракеты на орбиту

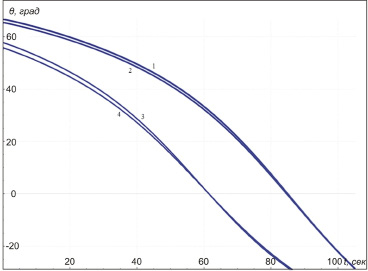
Рис. 4. Изменение оптимального угла действия тяги при выводе ракеты на орбиту

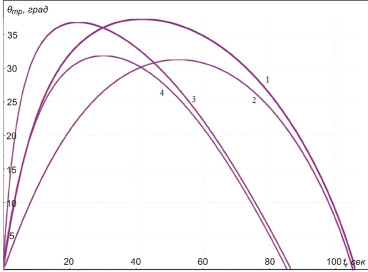
Рис. 5. Изменение траекторного угла при выводе ракеты на орбиту

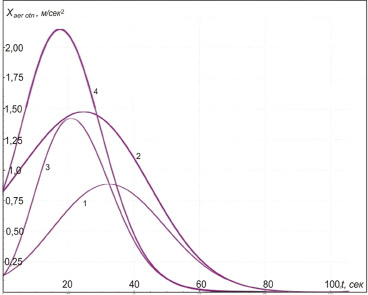
Рис. 6. Изменение величины относительного аэродинамического сопротивления Xaer / m (ускорения от силы аэродинамического сопротивления) при выводе ракеты на орбиту

Потребная для вывода на орбиту относительная масса топлива

Следует отметить, что такая пара окислитель – горючее, как кислород и водород, дающие импульс, близкий к 4000 м/с, может не обеспечить теоретического выигрыша, так как водород обладает низкой плотностью, что приведет к увеличению размеров топливных баков и изменению габаритов ракеты. Это может сказаться на ухудшении аэродинамических показателей и в результате на увеличении времени вывода ракеты на орбиту.