Для численного решения задачи Коши рассматриваются параллельные аналоги алгоритмов явных методов типа Рунге-Кутты для систем обыкновенных дифференциальных уравнений первого порядка. Предложены параллельные вычислительные схемы методов, ориентированных на применение в много процессорных вычислительных системах кластерной архитектуры.
Рассматривается задачи Коши для систем обыкновенных дифференциальных уравнений первого порядка
Для численного решения задачи (1) применяется явные s-стадийные методы типа Рунге-Кутты, (n + 1)-й шаг в которых задается формулами
где 
i=1,2,...,s
Конкретный метод Рунге - Кутты определяется набором коэффициентов bi, ci, ai, 1 ≤ i ≤ s, 2 ≤j ≤ (i - 1) [2-4].
Основной подход при конструировании параллельных методов состоял в распараллеливании последовательных численных алгоритмов, использовании декомпозиции и анализе информационных взаимосвязей между подзадачами [1, 5].
1. Последовательная вычислительная схема
Для определенности зададимся
некоторым отрезком [t0, T],
введем
равномерную сетку w = (t0,
t1,..., ts) с величиной шага hn+1= h и на сетке wn в начальный момент времени t0 в
качестве начального условия зададим вектор j(0) =
(y(0)1, y(0)2,..., y(0)N).
Определение
значений компонент вектора приближенного решения 
осуществляется по формуле (2), записанной для
вычисления каждой компоненты вектора y(n+1)
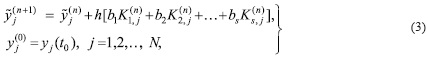
где 
Формулы (2) и (3) показывают, что определение значения у(n+1) сводится к строго последовательному вычислению коэффициентов К1(n), К2(n),..., Ks(n) их умножению на коэффициенты bi, i = 1, 2, ., s, соответственно, и последующему суммированию.
2. Параллельная явная s -стадийная вычислительная схема
Последовательная схема (3) дает основание для организации двух типов параллельных вычислений:
а) вычисление отдельных компонент векторов коэффициентов К1(n),K2(n),...,Ks(n) и вектора численного решения
б) вычисление отдельных операций внутри одного шага метода.
Вычисление отдельных операций
внутри одного шага метода обеспечивает небольшую степень
параллелизма и
поэтому не рассматривается.
С целью выявления максимального независимого набора операций при вычислении коэффициентов К1(n) , i=1,2,...,s используется аппарат графов зависимости. Анализ графа зависимостей, в предположении, что размерность N исходной системы (1) кратна числу компьютеров p, N = kp и схема размещения блочная обеспечивает возможность записи параллельных схем. В каждом компьютере размещено и вычисляется последовательно по k компонент векторов коэффициентов, K1(n), K2(n),...,Кs(n). Вычисления y(n+1) в n-м узле сетки wn реализуются по правилу, показанному ниже.
Вычисление коэффициентов и вектора приближенного решения при N = kp лгоритм. Пусть задана система (1), правая часть которой гладкая по всем аргументам yi, 1 ≤ i ≤ N и пусть на заданном отрезке [t0, T] определена равномерная сетка wn. Тогда для решения задачи Коши вычислительной системе из p = N/k компьютеров, Comp(i), 1 ≤ i ≤ N, и блочной схемой хранения, справедлив параллельный алгоритм.
Шаг 1. Вычислить К(n)1,lz и α(n)2,lz по формулам
и переслать K(n)1,lz и α(n)2,lz всем (p - 1) компьютерам.
Шаг 2. Вычислить K(n)2,lzи α(n)3,lzпо формулам
и переслать K(n)2,lz и α(n)3,lz всем (p - 1) компьютерам ....................................................
Шаг s. Вычислить K(n)s,lz
Шаг (s + 1). Вычислить
Шаг (s + 3). Переслать 
всем (p-1) компьютерам.
. Таким образом, после параллельного вычисления коэффициентов параллельно определяется
такое же количество компонент вектора приближенного решения Число
пересылок для одного узла сетки wn составит s(p - 1)2≈O(sp2).
Параллельный аналог формулы (3) для равномерной сетки может быть записан в виде
где 
Заметим, что в отдельных случаях, зависящих от типа и вида исходной системы (1), может быть достигнута максимальная степень параллелизма и, соответственно, сокращение временных затрат выполнения вычислений по разработанному алгоритму. Так, например, для двустадийной схемы Рунге-Кутты параллельный алгоритм записывается следующим образом.
Шаг 1. Вычислить
по формулам
Шаг 2. Вычислить 
по формулам
Шаг 3 Вычислить
Шаг 4. Сохранить 
Шаг 5. Переслать всем (p - 1) компьютерам.
Рассмотренные параллельные схемы явных методов типа Рунге-Кутты ориентированы на реализацию в многопроцессорных вычислительных системах кластерной архитектуры с использованием технологии MPI. MPI имеет в составе коммуникационные операции попарные и коллективные обмены, средства организации виртуальных топологий. Исследования представленных параллельных схем показали, что для их реализация наиболее подходящими могут быть топологии кольцо, линейка, решетка и гиперкуб. Разработанные схемы могут служить основой для разработки параллельных алгоритмов решения задачи Коши явными методами с контролем точности и устойчивости, алгоритмов переменного порядка и шага, а также возможной автоматизации построения методов интегрирования с адаптивной областью устойчивости.
Список литературы
1. Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. - СПб.: БХВ - Петербург, 2002. - 806 с.
2. Новиков Е.А. Явные методы для жестких систем. -Новосибирск: Наука, 1997. - 197 с.
3. Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. - М.: Мир, 1999. - 685 с.
4. Jackson K., Norsett S. The potential for parallelism in Runge -Kutta methods. Part I: RK formulas in standart form // SIAM J. Numer. Anal. - 1996.
- Vol. 32. - P. 49-82.
5. Hendrickson B., KoldaTamaraG.Graphpartitioningmodels for parallel computing // Parallel Computing.-2002.-Т. 26,№12.-P. 181-197.