Интегральные уравнения относятся к разделу математики и являются важными для приложений – к ним приводятся прикладные задачи разных разделов физики, техники и других многих наук. Поэтому в настоящее время теория интегральных уравнений интенсивно развивается благодаря исследователям. С развитием современных компьютерных технологий можно строить математические модели прикладных задач и решать их методами численных решений. Многие такие задачи сводятся к интегральным уравнениям. Для доказательства существования решения линейного интегрального уравнения Вольтерра первого рода с одной переменной и достаточными условиями для их получения А.М. Денисов, В.О. Сергеев и другие авторы использовали метод дифференцирования по заданным функциям [1, 2, 3]. В своих работах М.М. Лаврентьев, М.И. Иманалиев и А. Асанов изучали решение линейных интегральных уравнений первого рода [4, 5] в пространстве функций C(G) и обобщенных интегральных уравнений Вольтерра первого типа с негладким ядром. Первые результаты по построению регуляризации для решения интегральных уравнений Вольтерра первого рода с одним независимым переменным были получены в [1]. Однако интегральные уравнения с двумя независимыми переменными мало изучены. Это объясняется трудностями в построении резольвенты, так как еще не получено аналитическое представление в общем виде, за исключением некоторых случаев. Поэтому исследования решений таких уравнений являются актуальными.
В связи с этим данная статья посвящена изучению регуляризации для решения интегрального уравнения Вольтерра первого рода с двумя независимыми переменными. Основной целью данной работы является построение алгоритма регуляризации для решения интегрального уравнения [6, 7].
Материалы и методы исследования
В данном исследовании показаны материалы для важных разделов высшей математики, такие как теория обратных задач, где используются методы интегральных уравнений, функционального анализа, метод последовательных приближений и малого параметра, а также методы регуляризации и элементы математического и функционального анализов.
Результаты исследования и их обсуждение
Пусть задано уравнение вида
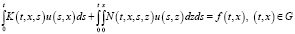 (1)
(1)
где u(t,x) – неизвестная функция, K(t,x,s) и N(t,x,s,z) – ядра, f(t,x) – известная функция,
f(t,x) = 0 при x∈[0;X], G ={(t,x): 0 ≤ t ≤ T, 0 ≤ x ≤ X}.
На основании выполнения условий:
а) K(t,x,s)∈G1={(t,x,s): 0 ≤ s ≤ t ≤ T, 0 ≤ x ≤ X}, N(t,x,s,z)∈G2={(t,x,s,z): 0 ≤ s ≤ t ≤ T, 0 ≤ z ≤ x ≤ X} – непрерывные функции, K(t,x,t) ≥ K0(t) >0 при (t,x)∈G, 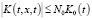 ,
, 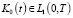 ;
;
б) при t>τ и для любых (t,x,s),(τ,x,s)∈G1 справедливо неравенство:
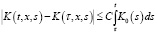 ,
,
где 0<C – const;
в) при t>τ для любых (t,x,s,z),(τ,x,s,z)∈G2 справедливо неравенство:
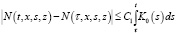 ,
,
где 0<C1 – const и 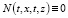 при G3={(t,x,s,z): 0 ≤ t ≤ T, 0 ≤ z ≤ x ≤ X};
при G3={(t,x,s,z): 0 ≤ t ≤ T, 0 ≤ z ≤ x ≤ X};
Вместе с уравнением (1) рассмотрим следующее сингулярно-возмущенное уравнение:
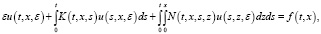 (2)
(2)
где 0<С – малый параметр.
В уравнении (2) сделаем подстановку:
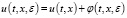 , (t,x)∈G. (3)
, (t,x)∈G. (3)
Подстановка (3), подставляем в (2), имеем:
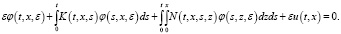
Из последнего уравнения имеем следующее равенство:
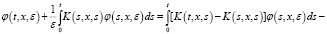
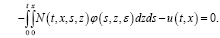 (4)
(4)
Применяя резольвенту ядра 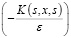
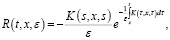
из (4) имеем:
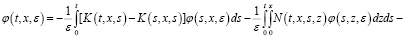
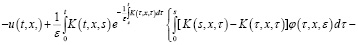
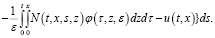
Относительно этого уравнения делаем соответствующие несложные преобразования:
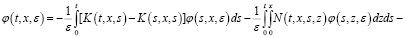
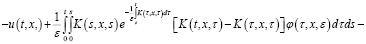
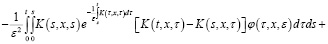
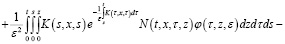
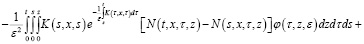
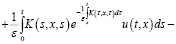
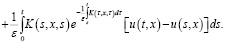
Учитывая, что 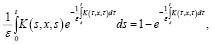 и применяя формулу Дирихле, из последнего уравнения получаем:
и применяя формулу Дирихле, из последнего уравнения получаем:
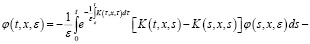
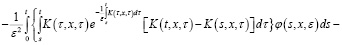
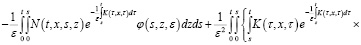
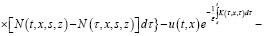
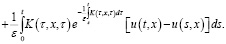
Отсюда:
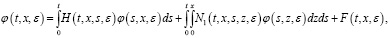 (5)
(5)
где 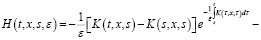
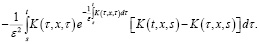 (6)
(6)
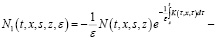
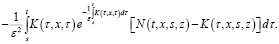 (7)
(7)
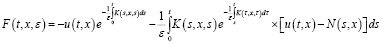 . (8)
. (8)
Для доказательства последнего равенства предварительно докажем следующую лемму.
Лемма 1. Пусть выполняется следующее равенство:
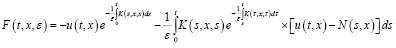 .
.
где 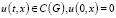 при
при 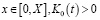 при всех
при всех 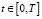 ,
,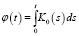 .
.
Тогда справедлива следующая оценка:
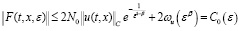 ,
,
где β∈(0,1), 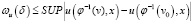 .
.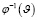 – обратная функция к функции
– обратная функция к функции 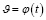 .
.
Доказательство.
а) Если 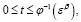 то из (8) получаем:
то из (8) получаем:
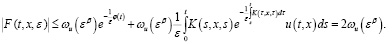 (9)
(9)
б) Если 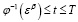 , то имеем
, то имеем
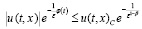 ; (10)
; (10)
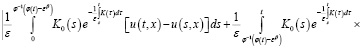
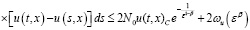 , (11)
, (11)
из (9), (10) и (11) получаем справедливость леммы 1.
Лемма 2. Пусть функция 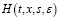 определена в равенстве (6) и выполняются условия а) и б). Тогда справедлива оценка:
определена в равенстве (6) и выполняются условия а) и б). Тогда справедлива оценка: 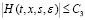 , где С3=С(N0+е-1).
, где С3=С(N0+е-1).
Доказательство. Применяя условие б) из (6), имеем неравенство:
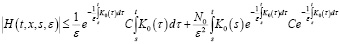
Для первого слагаемого имеем следующее неравенство:
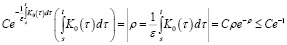
А для второго слагаемого справедливо соотношение:
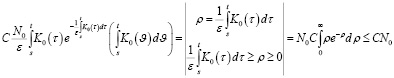
Следовательно, справедлива лемма 2.
Лемма 3. Пусть функция 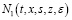 определяется из равенства (7). Если выполняются условия а) и в), то справедлива оценка
определяется из равенства (7). Если выполняются условия а) и в), то справедлива оценка 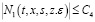 , где С4=С2(N0+е-1).
, где С4=С2(N0+е-1).
Доказательство. Принимая условия а) и в) из (7), получаем требуемую оценку.
Далее, в силу лемм 1, 2 и 3 из (5) получим:
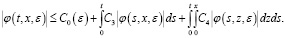
Отсюда, введя следующую подстановку:
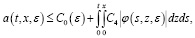 (12)
(12)
имеем неравенство
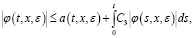 (13)
(13)
В дальнейшем используем следующие леммы [2].
Лемма 4. Пусть 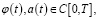 a(t)≥0 при
a(t)≥0 при 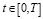 ,
,
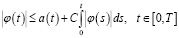
где 0<C6– const. Тогда справедливо следующее неравенство:
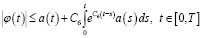
Лемма 5. Пусть 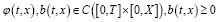 и
и
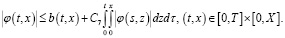
где 0<C7 – const.
Из последнего соотношения получаем следующее неравенство:
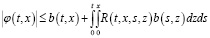
где 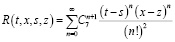 .
.
Доказательство
Пусть 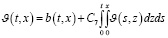 ,
, 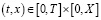 .
.
Отсюда, применяя метод последовательных приближений, имеем:
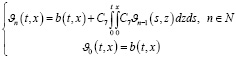
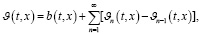 (14)
(14)
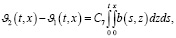
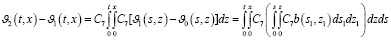
В последнем равенстве, применяя формулу Дирихле, получаем:
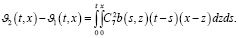
Используя метод математической индукции, получим:
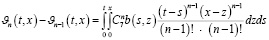
Тогда из (14) получаем:
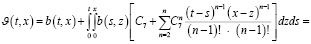
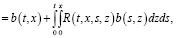
где 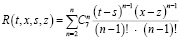 .
. 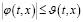 ,
, 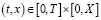 .
.
Лемма 6 доказана.
Далее, применяем лемму 5 к неравенству (13), получим:
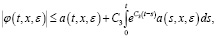 (15)
(15)
Подставляя (13) в (15), имеем:
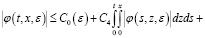
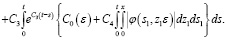
Здесь, интегрируя и применяя формулу Дирихле, получаем:
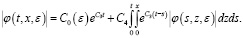
Затем заменив t на Т, имеем:
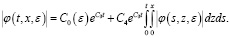 (16)
(16)
На равенство (16), используя лемму 5 и формулу Дирихле, получим:
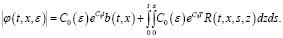 (17)
(17)
где 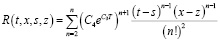 .
.
Из (17) вытекает следующее равенство:
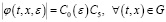 , (18)
, (18)
где 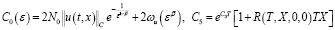 ,
,
доказана следующая теорема.
Теорема. Пусть выполнятся условия а)–в) и уравнение (1) имеет непрерывное решение u(t,x) на G и u(0,x)=0 при x∈[0;X]; K0(t)>0 почти для всех t∈[0;T]. Тогда решение уравнения (2) можно представить в виде (3), и это решение приближается к непрерывному решению уравнения (1) в области G на ε→0, и оценка (18) верна.
Следствие. Если 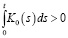 при всех t∈[0;T] и выполняются условия а)–в).
при всех t∈[0;T] и выполняются условия а)–в).
Тогда решение уравнения (1) в пространстве C(G) единственно.
Доказательство. Пусть 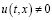 решение (1), при
решение (1), при 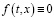 . Тогда из условий а)–в) можно показать, что
. Тогда из условий а)–в) можно показать, что 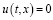 на x∈[0;X]. На самом деле, пусть имеем:
на x∈[0;X]. На самом деле, пусть имеем:
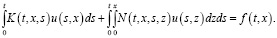
Преобразуем его в эквивалентное уравнение:
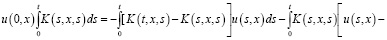
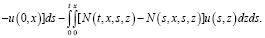
Согласно условиям а)–в) и по формуле Дирихле, заменяя τ на s, и на основании теоремы о среднем значении имеем:
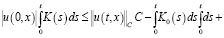
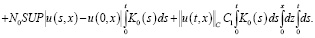
По условию теоремы 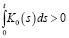 при всех
при всех 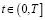 . Поэтому имеем:
. Поэтому имеем:
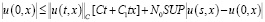 .
.
Отсюда, переходя к пределу, при t→0 получим u(t,x)=0 для x∈[0;X]. Ясно, что если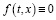 то
то 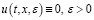 , где
, где 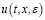 – решение уравнения (2).
– решение уравнения (2).
Далее в силу теоремы имеем:
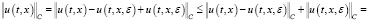
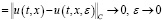 . т.e.
. т.e. 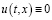 при почти всех (t,x)∈G.
при почти всех (t,x)∈G.
Заключение
В данной работе рассмотрено интегральное уравнение Вольтерра первого рода с двумя независимыми переменными. Установлены достаточные условия единственности и построен алгоритм регуляризации для решения интегрального уравнения Вольтерра первого рода с двумя независимыми переменными в пространстве C(G). Результаты работы могут применяться в прикладных задачах, где вырождаются нелинейные некорректные интегральные уравнения первого рода.

