В международной системе единиц (СИ) [1, с. 25] указано, что единица измерения телесного угла не имеет размерности. Однако авторский метод двухкоординатной равновеликой развертки позволяет предложить и размерность, и способ ее количественного измерения [2].
Созданный в целях развития теории начертательной геометрии авторский метод проекций с временными отметками дал возможность количественно решать пространственно-временные задачи с 7 и более числом переменных [3].
Манипуляции с графиками функций дали возможность не только создать графическую теорию мнимых чисел, которая подтверждена сечениями геометрических тел (конусов вращения), но и предложить общие математические зависимости описания некоторых «замечательных» кривых: эллипса, гиперболы и окружности [4-6].
Сугубо графическая интерпретация тригонометрических функций (синуса и косинуса) позволила создать графическую теорию, позволяющую осуществлять с ними арифметические операции сложения/вычитания, но также, что более важно, суммировать и синусоиды [7]. Метод подтвержден графическими расчетами в области теоретической электротехники [8].
Изложенные результаты графических исследований позволили обобщить их термином «вычислительная графика» [9]. Изложению методики этой дисциплины на примере решения систем уравнений посвящена данная публикация.
Материал и методы исследования
Задача 1. Решить систему трех уравнений с тремя неизвестными (1).
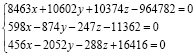 (1)
(1)
Математическое решение получено вычислением определителей [10]. Приведем вычисление одного из них:
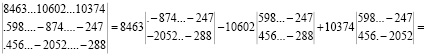
=8 463(874*288-2052*247)-10 602(-598*288+456*247)+10 374(-598*2 052 +456*874) = = 8 463(251 712+506 844) – 10 602(-172 224+112 632) + 10 374 (-1 227 096+398 544) = = 8463*255 132 + 10 602*59 592 – 10 374*828 552 = = 2 159 182 116 + 631 794 384 – 8 595 398 448 = 10 122 786 180.
Численные значения других определителей соответственно равны:
∆х = 559 186 117 776;
∆y= 160 094 410 476;
∆z = 321 627 997 380.
Арифметические действия с определителями дали численные значения решения:
x =55,239302;
y = 15,816078;
z = 31,772765.
Учитывая то, что каждое уравнение первой степени с тремя неизвестными представляет собой плоскость, графическое решение сводится к построению линии их пересечения.
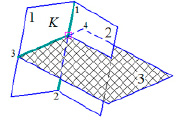
Рис. 1. Обоснование графического решения
Методика решения (рис. 1) состоит в построении линий пересечения плоскостей 1 и 2 (отрезок 1-2), а также 1 – 3 (отрезок 3-4). Ответом является точка пересечения отрезков 1-2 и 3-4.
Реализация методами начертательной геометрии выполнена в следующем порядке. Во-первых, все уравнения преобразованы в «уравнения плоскости в отрезках» [11]. Во-вторых, каждое уравнение на чертеже (рис. 2) изображено следами плоскостей (изображены тонкими линиями) по точкам их схода.
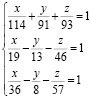
Линия пересечения плоскостей 1 и 2 (стиль – основная линия) построена по проекциям точек 1 и 2 (обозначены кружками) пересечения следов.
Фронтальная проекция линии пересечения плоскостей 1 и 3 (а для решения достаточно только ее) 32 – 42 (стиль – утолщенная линия) также построена по точкам пересечения следов 41 и 32 (отмечены кружками).
Ответом является точка пересечения (К – обозначена квадратом) проекций отрезков 1-2 и 3-4.
Измерением по чертежу координат точки К средствами компьютерной графики нашли те же значения (шесть знаков после запятой), что приведены выше, но полученные математическим путем [12].
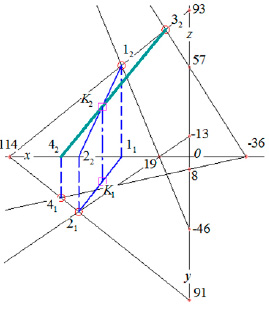
Рис. 2. Графическое решение системы уравнений (1)
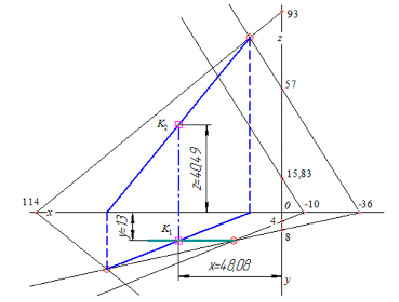
Рис. 3. Графическое решение системы уравнений (2)
В качестве примечания отметим, что в графическом варианте без дополнительных построений число знаков после запятой можно увеличить [13].
Сравним рассмотренные варианты по разным критериям.
Универсальность. Явное преимущество имеет математический способ.
Количество логических операций. В математическом методе их более 100. Это умножение, сложение, вычитание, раскрытие скобок со сменой знака. В графическом варианте: построение точек по координатам – 9, построение отрезков по точкам пересечения – 6.
Из сопоставления можно сделать вывод. Для массового применения практичнее составить и апробировать универсальную математическую программу. В конструкторской практике, при разовом использовании, более удобен графической вариант.
Особенность графического решения, помимо очевидной простоты и логичности, состоит в возможности быстрого решения одной задачи с изменяющимися параметрами.
Задача 2. Решить систему уравнений (1) с измененными условиями.
В качестве примера, в подтверждение сказанного, на рисунке 3 показано решение системы (2), в которой по сравнению с (1) целиком заменено 2-е уравнение.
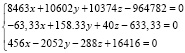 (2)
(2)
При сохранении изображения плоскостей 1 и 3 вместе с линией их пересечения решением является построение следов новой плоскости и линии пересечения ее с первой плоскостью. Ответ – координаты точки пересечения двух отрезков.
В данном примере для получения ответа потребовалась лишь одна проекция искомой линии, поскольку учтена параллельность фронтальных следов, как это использовано при решении аналогичной задачи в учебнике [14].
Данные графические процедуры можно проводить неограниченное число раз, изменяя последовательно либо один параметр, либо уравнение в целом. Такое возможно, например, при поиске оптимального варианта исходных параметров. Расширительно подобное решение можно толковать как своеобразную графическую программу.
Так на примере решения задач на определение корней системы уравнений с тремя неизвестными графическим способом в системе Компас 3D показано преимущество графического способа решения, которое состоит в следующем.
1. Высокая точность вычислений – до 8-го знака после запятой.
2. Простота построений с применением метода проецирования, которая позволяет затратить меньше времени на решение задачи.
3. Возможность многовариантного решения, заложенная в самом графическом построении, где изменение условий легко реализуется и позволяет получить новый результат.
4. Сокращение количества этапов решения, что оптимизирует временные затраты и делает метод более простым для решения.
5. Универсальность в применении графического метода для решения любых математических задач.
Заключение
Вычислительная графика, обладающая вышеперечисленными преимуществами, является перспективной областью развития научных исследований, ее возможности могут быть применены в смежных областях знаний, например в разделах теоретической механики, электротехники, при изучении материаловедения, выполнении различных технических прочностных расчетов, при изучении сопротивления материалов, деформации, и в других общеобразовательных и общетехнических областях научной деятельности.
Графические способы решения вырабатывают навыки визуального восприятия информации, замены привычных формул графическими объектами, изучение и восприятие которых способствуют развитию пространственного мышления – навыка, востребованного в практической инженерной деятельности. Работа с графической информацией – составляющая часть деятельности при проектировании, на стадии разработки технологии и в производстве любого технического объекта [15]. Сочетание математических расчетов с графическими построениями развивает способности специалистов технического профиля к решению возникающих задач нестандартным путем с минимальными временными затратами и оптимальным способом.

