Количественное измерение неровностей поверхности является важной практической задачей во многих областях научно-технической деятельности: приборостроении, нано- и микроэлектронике, методах космического зондирования земных покровов и т.д. Особую роль среди способов определения шероховатости поверхности играют бесконтактные методы контроля, использующие для облучения исследуемого объекта удаленный источник электромагнитных волн (ЭМВ) и соответствующий приемник сигналов. Как правило, форма отражающей поверхности нерегулярна, а высота точек поверхности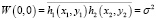 
является случайной функцией ее координат. Эту случайную поверхность характеризует корреляционная функция (КФ), которая определяется как средняя от произведения ординат двух различных пространственно разнесенных точек поверхности: 
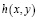, где σ – среднее квадратическое отклонение высот от среднего уровня поверхности. На практике часто бывает необходимо знание и другого параметра шероховатости – интервала (радиуса) корреляции Т – характерного расстояния, на котором КФ W поверхности существенно меняется. Величина Т зависит от отношения σ к длине волны излучения λ. Электромагнитное поле, рассеянное на поверхности, также является случайной функцией пространственных координат и времени. Ансамбль реализации этой случайной функции есть совокупность ЭМВ, возникающих при дифракции на неровностях поверхности. Поэтому свойства дифференциальной функции распределения вероятностей значений амплитуд рассеянного поля в разных точках пространства аналогичны свойствам плотности распределения высот неровностей поверхности. Актуальной является следующая задача: по статистике рассеянных ЭМВ определить параметры шероховатостей и их влияние на рассеяние сигналов.
Метод, основанный на анализе индикатрис рассеянного света, является весьма эффективным для определения электрооптических и геометрических характеристик поверхностей. В большинстве случаев эти параметры поверхности измеряются в независимых экспериментах, а способ определения параметров шероховатостей с использованием разных наборов корреляционных функций не всегда отличается корректностью.
В настоящей работе предлагаются эффективный метод определения корреляционной функции (КФ) сверхгладкой поверхности с помощью описанного ранее [1] поляризационного рефлектометра, а также способ нахождения на том же приборе среднеквадратического отклонения высот неровностей σ2, корреляционной длины T и диэлектрической постоянной ε приповерхностных слоев.
Подход основан на выводах теории малых возмущений, применимой при малых флуктуациях параметров среды и малых интенсивностях рассеянного света по отношению к интенсивности падающего. В качестве одного из важных критериев применимости этого приближения, определяющего способ определения неровностей и степень их влияния на характеристики отражения и рассеяния, используется известный критерий σ / λ << 1.
Согласно теории рассеяния, интенсивность I диффузной составляющей отраженного от поверхности образца света c длиной волны λ >> σ пропорциональна оптическому фактору Q, зависящему от величины ε и геометрии опыта, а также спектральной плотности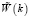 
КФ W(ρ) [2]:
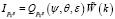(1)
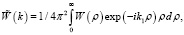(2)
где ρ и k – модули радиус-вектора частицы и разности волновых векторов рассеянного и падающего света,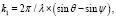 
индексы p и s отличают p и s – поляризацию, ψ и θ – углы падения и рассеяния. Используя выражение (1), можно получить данные о параметрах шероховатостей поверхности образца, связанные с видом КФ (множитель 
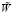), или диэлектрической проницаемости ε (значение Q). Рассмотрим оба случая по отдельности.
Определение КФ и параметров шероховатостей поверхности
Как известно, существуют по меньшей мере два метода нахождения КФ [2, 3] из эксперимента по рассеянию света. Первый метод состоит в подборе КФ из набора заданных аналитических выражений с последующим вычислением интеграла (2). Сравнивая затем полученную теоретическую зависимость I(θ) с экспериментальной индикатрисой рассеяния, выбирают ту КФ, которая лучше описывает эксперимент. Второй метод заключается в вычислении функции W(ρ) как преобразования, обратного (2), и дальнейшей ее аппроксимации. Недостатками этих методов являются, соответственно, неоднозначность в выборе КФ, зависящей от параметров шероховатостей, и необходимость знать индикатрису рассеяния во всей полусфере, так как Фурье-преобразование предполагает интегрирование по всей области определения ρ. В большинстве экспериментов рассеянное излучение измеряется в плоскости падения, поэтому данных эксперимента не хватает для определения W(ρ) из обратного Фурье-преобразования (2). Рассмотрим другое решение этой задачи.
Уравнение (2) является, по сути, однородным уравнением Фредгольма второго рода, в котором W(ρ) является искомой функцией, а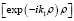 
– ядром. Представим КФ W(ρ) в виде ряда по системе ортогональных функций Jj(ρ) j-го порядка:
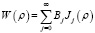, (3)
где Bj – коэффициенты разложения, которые необходимо найти. Подставив уравнение (3) в (2), получим:
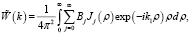(4)
Поменяв местами порядок суммирования и интегрирования, будем иметь:
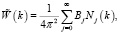(5)
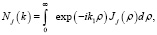(6)
есть Фурье-образы выбранных функции Jj(ρ). В качестве системы данных ортогональных функций J возьмем модифицированные функции Лагерра:
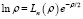. (7)
Фурье-образами (6) этих функций являются многочлены Якоби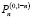 
, составляющие также ортогональную систему с весовой функцией f(ρ):
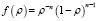. (8)
Теперь уравнение (5) будет иметь вид:
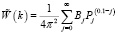. (9)
Откуда, используя ортогональность функций Якоби, можно определить коэффициенты Bj:
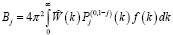. (10)
Минимизируя по параметрам Bj разницу между экспериментальной индикатрисой и кривой, рассчитанной с использованием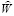 
из (9), получим искомые коэффициенты разложения КФ. Подставляя их в уравнение (3), найдем W(ρ). Данный способ определения КФ достаточно корректен и упрощает эксперимент.
Параметры шероховатостей σ2 и T могут быть найдены из известных условий нормировки, накладываемых на КФ:
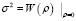. (11)
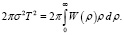
Предлагаемый способ определения КФ и параметров шероховатостей поверхности, а также методика измерений реализованы на описанной ранее в [1] установке. Объектами исследования служили отполированные кварцевые пластины, а также стеклянные подложки (основы магнитооптических дисков для записи и считывания информации).
На рисунке показаны результаты минимизации функции (Iэксп. – Iтеор.) для света λ = 0,628 мкм), рассеянного полированной поверхностью кварцевой пластинки. Видна очень хорошая сходимость процесса, что позволило достаточно быстро получить значения КФ и параметров шероховатостей поверхности: σ2 = 0,0030 мкм, Т = 1,6 мкм. Близкие значения этих параметров получены независимым методом при сканировании поверхности данного образца на лазерном интерференционном профилометре [4].
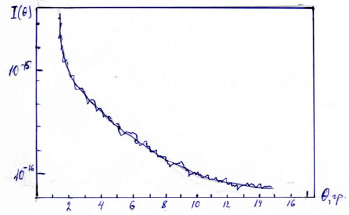
Экспериментальная индикатриса рассеяния и кривая, полученная в результате минимизации функции (Iэксп. – Iтеор.) для полированной пластины кварца
Определение диэлектрической проницаемости поверхности
Поскольку пространственный спектр высот неровностей поверхности не зависит от условий поляризации падающего света, то, вычисляя по (1) отношения интенсивностей s- и р-рассеянного света, мы получим простую формулу для определения из эксперимента величины ε при заданных углах падения и рассеяния света:
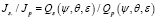, (12)
где, как известно:
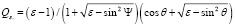, (13)
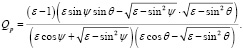(14)
Прибор устроен таким образом, что анализируется только свет, рассеянный от передней грани прозрачного образца. Измеренные в разных точках исследуемой поверхности отношения интенсивностей Is / Ip в пределах 10%-ной ошибки оказались примерно одинаковыми. Это позволило найти среднее по образцу значение диэлектрической постоянной приповерхностного слоя. Для отполированных пластинок кварца и стекла эти значения равны 2,33 и 1,83, что меньше значений ε в объеме (2,40 и 2,18 соответственно), определенных при той же частоте падающего света. Уменьшение величины ε на поверхности по сравнению с объемом может быть обусловлено релаксацией и реконструкцией поверхности вследствие изменения структуры и внутреннего поля, а также обработки образца [5].
Данный способ определения корреляционной функции и параметров шероховатостей поверхности с использованием экспериментальной индикатриссы рассеяния может быть использован для любого типа границ раздела при соблюдении критерия Рэлея, определяющего степень неровностей поверхности отражения. Если условие Рэлея σ / λ < 1 / (16 sinψ) (где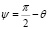 
– угол скольжения) выполняется, то отражающую поверхность можно считать квазигладкой (набег фаз на возмущениях σ чрезвычайно мал), и тогда выводы лежащей в основе метода теории малых возмущений справедливы в полной мере. Способ может применяться не только для объектов с нанометровыми шероховатостями, облучаемых светом, но и, например, в радиолокационных методах зондирования земных покровов сигналами навигационных спутников L-диапазона. Следует отметить, что отраженная электромагнитная волна формируется не в одной точке, а в пределах области, ограниченной первой зоной Френеля, где излучение когерентно. Именно в пределах этой области необходимо учитывать степень шероховатости отражающей поверхности.