Представляет интерес использование солнечного паруса в межпланетных перелетах. Возможность осуществления межпланетных перелетов без затрат топлива очень привлекательна, но возникает ряд проблем при ее реализации. Давление света мало и уменьшается при увеличении расстояния от Солнца. В силу этого размер солнечного паруса должен быть достаточно большим и он должен быть изготовлен из сверхлегкого материала. Первым успешным проектом был японский IKAROS [1], запущенный в 2010 г. Одним из успешных американских проектов является аппарат LightSail-2 [1]. Разработки солнечного паруса ведутся в настоящее время и в России. Появились работы по численному моделированию и оптимизации перелетов малых космических аппаратов (КА) под солнечным парусом или с использованием ионных двигателей в пределах Солнечной системы [2, 3].
Цель исследования – провести оптимизацию управления солнечным парусом в межорбитальном перелете между орбитами Земли и Венеры, тем самым проверить возможность осуществления перелета к планете, находящейся на более близкой к Солнцу орбите, при помощи солнечного паруса. Расчетное исследование планировалось провести, используя принцип максимума Понтрягина численным методом пристрелки.
Постановка задачи оптимизации, математическое моделирование межорбитального перелета и применяемые численные методы
Постановка задачи и уравнения движения соответствуют [4]. Задача оптимального управления (ОУ) углом солнечного паруса при движении КА в солнечной системе решается при использовании принципа максимума Понтрягина. Эта задача сводится к краевой задаче системы обыкновенных дифференциальных уравнений. Для численного решения краевой задачи часто прибегают к методу вариации управлений. В данной работе был применен метод пристрелки. Метод пристрелки обладает рядом преимуществ и недостатков. С одной стороны, он наиболее точен при численном решении краевых задач [5], с другой – возникают определенные сложности при подборе начальных значений параметров пристрелки, особенно при размерности системы ДУ больше 4. Однако трудности в реализации этого расчетного метода при наличии опыта работы с методом Ньютона могут быть преодолены как для задач без ограничения на управление, так и для задач ОУ с переключением [5–7]. Оптимизации управления солнечным парусом посвящены также и работы [8–10].
За критерий эффективности принимается время перелета, то есть используется функционал вида 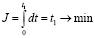 .
.
При моделировании движения КА принимались некоторые упрощения:
− рассматривается гелиоцентрический участок перелета между орбитами, притяжениями планет пренебрегается,
− предполагается, что орбиты планет круговые и что они лежат строго в одной плоскости.
Система состояния (система ОДУ движения космического аппарата под солнечным парусом) расписана в гелиоцентрической полярной системе координат:
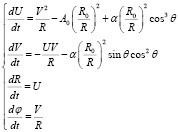 .
.
где t1 – время перелета между орбитами, с; t – текущее время, с; R0, R – радиусы (расстояние между Солнцем и КА в начальный момент и в текущий соответственно), м; А0 – ускорение КА от силы тяготения Солнца в начальный момент перелета, м/с2; α – ускорение КА от давления света в начальный момент перелета, м/с2; U – составляющая скорости КА, направленная вдоль радиуса (рис. 1), м/с; V – составляющая скорости КА, перпендикулярная радиусу, м/с; φ – угол КА в полярной гелиоцентрической системе координат, рад; θ – управление в задаче ОУ, угол установки солнечного паруса (рис. 1), рад. В соответствии с принятой математической моделью в [4] положительные углы θ принято измерять по часовой стрелке от направления тангенциальной скорости КА, отрицательные – против часовой стрелки. Естественное ограничение на угол 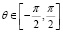 .
.
На рисунке 1 Т – сила действия солнечного паруса, угол установки которого отрицателен. Естественное ограничение на угол 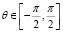 .
.
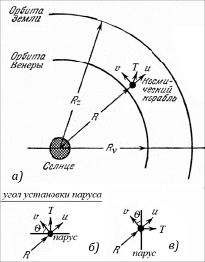
Рис. 1. а) схема перелета с указанием положительного направления скоростей, б) отрицательный угол установки паруса, в) положительный угол установки паруса
Для решаемой задачи ОУ были приняты следующие краевые условия. V0 = Vz, U0 = Uz = 0, R0 = Rz, φ0 = φz = 0 – соответственно в начальный момент времени: значение тангенциальной скорости КА, равной скорости движения Земли по ее орбите, значение составляющей скорости КА вдоль радиуса, радиус КА, равный радиусу земной орбиты, а также полярный угол, Vf = Vv, Uf = Uv = 0, Rf = Rv – соответственно в момент окончания перелета: значение тангенциальной скорости КА, равной орбитальной скорости Венеры, значение радиальной скорости КА, радиус орбиты Венеры.
Функция Понтрягина в задаче быстродействия в данной постановке задачи:
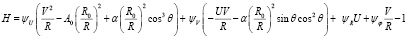 .
.
где ψU, ψV, ψR, ψφ – сопряженные переменные.
Максимум функции Понтрягина по управлению определяется из
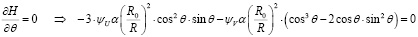 .
.
Решение этого уравнения позволяет получить тангенс оптимального угла установки солнечного паруса:
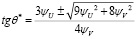 .
.
Отметим, что при одновременной смене знаков у ψU и ψV одно решение переходит в другое. Решение было найдено для варианта с минусом перед выражением под квадратным корнем, при этом функция Понтрягина оставалась постоянной и равной нулю с точностью до пятого знака на всей найденной экстремали, что соответствует необходимому признаку существования ОУ для автономной системы уравнений движения и свободном времени на конце процесса. При выборе ψU и ψV отрицательными в начальный момент времени получим формулу для отыскания оптимального угла установки солнечного паруса:
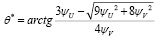 .
.
Анализ полученной формулы показывает, что оптимальный угол установки паруса может находиться только в одной четверти (в первой для уменьшения радиуса орбиты и в четвертой для увеличения). Переход через 0° при конечных ненулевых значениях ψV неосуществим, через +90° или -90° невозможен в силу наложенных ограничений.
Система ДУ для сопряженных переменных:
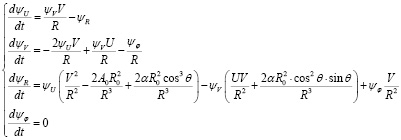 .
.
Имеем естественное краевое условие ψφ(t1) = 0.
Отсюда можем исключить из системы ДУ ψφ.
Преобразованная П-система состоит из семи уравнений:
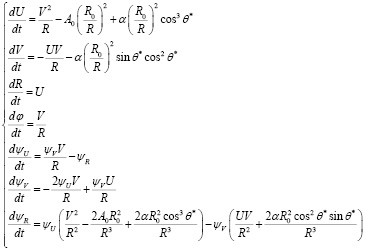 .
.
В методе пристрелки недостающие краевые условия называются параметрами пристрелки, задаются приближенно, таким образом, получаем задачу Коши для системы ОДУ. В дальнейшем значения параметров пристрелки уточняются численным методом Ньютона. В работе использовался модифицированный метод Ньютона, который подразумевает линеаризацию функций-невязок и оптимизацию ньютоновского шага в найденном направлении. Полученная при линеаризации функций-невязок СЛАУ решалась методом LU-разложения. При отыскании функций невязок был применен численный метод интегрирования системы ОДУ Рунге – Кутты 4-го порядка. Количество шагов было выбрано N = 1000. При выборе величины шага в ньютоновском направлении использовалась так называемая локальная норма, введенная в [5], вычисляемая как
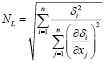 .
.
Такой подход позволяет улучшить сходимость метода Ньютона при различающихся на порядок или более невязках и их производных.
Для удобства выхода из метода численного интегрирования был введен дополнительный параметр пристрелки – t1, суммарное время перелета. Соответственно с этим изменением была преобразована П-система (введен новый аргумент: 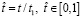 ).
).
Параметры пристрелки задачи ОУ:
ψU, ψV, ψR, t1.
Невязки, получаемые в конце интегрирования системы ДУ:
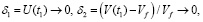
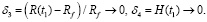
Результаты расчета
Начальные значения параметров пристрелки были выбраны: ψU = –700, ψV = –1300, ψR = –10–5, T = 200. На рис. 2 представлен график изменения радиальной скорости КА в процессе перелета. На рис. 3 – график изменения тангенциальной скорости КА. На рис. 4 и 5 – изменение расстояния от Солнца до КА и полярного угла соответственно. На рис. 6 представлено оптимальное значение угла установки солнечного паруса в процессе перелета. Для сравнения на рис. 7 приведено изменение по времени оптимального угла установки солнечного паруса при перелете на орбиту Марса, полученное в [11].
Найденные в процессе оптимизации значения сопряженных переменных в начале перелета имеют следующие значения: ψU(0) = –771,62, ψV = –3562, ψR = 0,0006153. Минимальное время перелета – 205,03 суток.
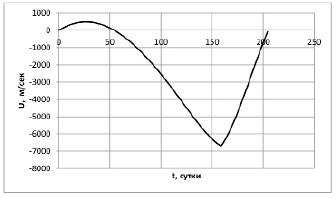
Рис. 2. Радиальная скорость КА при оптимальном управлении солнечным парусом при перелете на орбиту Венеры
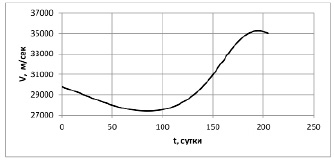
Рис. 3. Тангенциальная скорость КА при оптимальном управлении солнечным парусом при перелете на орбиту Венеры
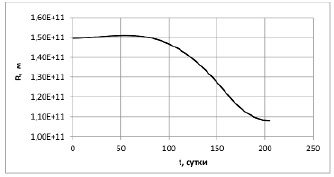
Рис. 4. Изменение расстояния от Солнца до КА при оптимальном управлении солнечным парусом при перелете на орбиту Венеры
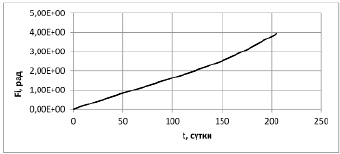
Рис. 5. Полярный угол при оптимальном управлении солнечным парусом при перелете на орбиту Венеры
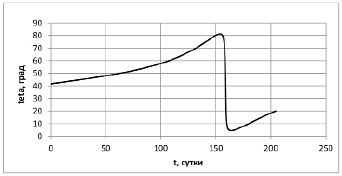
Рис. 6. Оптимальное управление (угол установки солнечного паруса) при перелете на орбиту Венеры
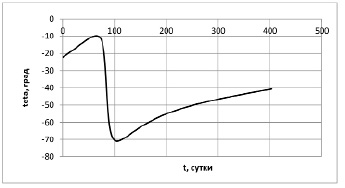
Рис. 7. Оптимальное управление (угол установки солнечного паруса) при перелете на орбиту Марса
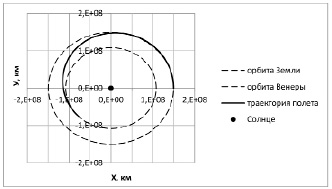
Рис. 8. Оптимальная траектория движения КА
На рис. 8 показана траектория КА в Солнечной системе.
Интересным представляется анализ поведения оптимального угла установки солнечного паруса с течением времени перелета. Примерно на 160 сутки перелета происходит резкое изменение угла установки паруса, что позволяет провести параллель с решением задач с переключением управления.
Заключение
По результатам проведенного расчетного исследования может быть сделан вывод о возможности осуществления гелиоцентрической части перелета КА малой массы с орбиты Земли на орбиту Венеры при помощи солнечного паруса и найден закон оптимального управления углом установки паруса. Необходимо затормозить скорость движения КА по орбите, чтобы влияние силы притяжения Солнца привело к уменьшению расстояния от КА до Солнца. Для этого нужно установить солнечный парус при положительных углах по отношению к тангенциальной составляющей скорости КА. Подтверждена работоспособность численного метода решения краевых задач, метода пристрелки при решении задач ОУ с нелинейными системами ОДУ. Введенное ограничение на углы установки паруса не повлияло на результаты расчета.

