Линейное программирование (ЛП) является методом математического программирования, использующимся для оптимизации линейной целевой функции при наличии линейных ограничений. Вот некоторые типичные задачи, которые можно решать с помощью линейного программирования:
1. Максимизация прибыли: найти оптимальное распределение ресурсов, чтобы максимизировать прибыль предприятия, учитывая ограничения на производство и рыночные условия.
2. Минимизация затрат: определить оптимальное распределение ресурсов для минимизации затрат при выполнении определенных требований и ограничений.
3. Распределение ресурсов: распределить ограниченные ресурсы (например, рабочую силу, сырье или мощности) между различными задачами или проектами таким образом, чтобы достичь наилучшего использования ресурсов и минимизировать затраты.
4. Планирование производства: определить оптимальный план производства, учитывая ограничения на доступность ресурсов, объемы производства и спрос на конечные продукты.
5. Транспортная задача: найти оптимальный план перевозки товаров из множества источников в множество пунктов назначения с минимальными затратами или максимизацией объемов перевозки.
6. Формирование портфеля: определить оптимальное распределение средств между различными финансовыми инструментами (акции, облигации, депозиты и т.д.) с целью минимизации риска или максимизации ожидаемой доходности;
7. Расписание: создать оптимальное расписание, учитывая ограничения по времени, доступность ресурсов и потребности клиентов.
8. Смешанная задача: решить задачу, которая содержит как линейные, так и нелинейные компоненты, путем линеаризации нелинейных ограничений и использования методов линейного программирования для нахождения приближенного решения.
Это лишь некоторые примеры задач, которые могут быть решены с использованием линейного программирования. ЛП находит широкое применение в различных областях, включая экономику, производственное планирование, логистику, финансы, транспорт и др.
Pyomo – это свободно распространяемый Python-пакет для моделирования и оптимизации математических моделей, в том числе линейного программирования, целочисленного линейного программирования, квадратичного программирования, динамического программирования и т.д. Pyomo обеспечивает удобный интерфейс для формулирования оптимизационных задач с помощью Python и является гибким инструментом для решения широкого спектра оптимизационных задач. Pyomo поддерживает различные солверы, включая open-source CBC, GLPK, IPOPT и Gurobi, а также коммерческие солверы CPLEX и GUROBI, что делает его очень гибким и подходящим для решения различных оптимизационных задач.
Pyomo использует язык моделирования для описания оптимизационных задач, который основан на языке AMPL. Pyomo поддерживает несколько способов задания моделей, включая модель в прямой форме, каноническую форму и др. Pyomo также позволяет использовать различные способы задания ограничений, переменных и функций целей.
Преимущества Pyomo:
− простота в использовании и понимании;
− возможность использования различных языков программирования для построения моделей;
− гибкость в настройке и выборе солвера;
− расширяемость и поддержка различных моделей, включая линейное программирование, целочисленное линейное программирование, квадратичное программирование, динамическое программирование и т.д.
− поддержка визуализации и анализа результатов оптимизации
Цель исследования – решить задачу линейного программирования с помощью библиотеки Pyomo на языке Python.
Материалы и методы исследования
Рассматривается задача упрощенного типа перевозки. У нас есть множество клиентов натуральных безалкогольных напитков (НБН) [1] I = {1, 2, 3, 4, 5} и множество предприятий по производству НБН J = {1, 2, 3}. У каждого покупателя есть фиксированная потребность в натуральных безалкогольных напитках pi , и у каждого предприятия есть фиксированная производственная мощность Mj. Также существуют фиксированные транспортные расходы на доставку одной единицы товара с производства j покупателю i.
Математически эту задачу оптимизации можно описать следующим образом:
Найти минимум
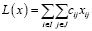 (1)
(1)
при условиях
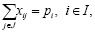 (2)
(2)
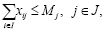 (3)
(3)
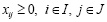 . (4)
. (4)
Теперь условия задачи (1)–(4) можно записать в виде таблицы.
Исходные данные
|
Покупатель i |
|||||||
|
Транспортные расходы cji |
1 |
2 |
3 |
4 |
5 |
Производственная мощность Mj |
|
|
НБН j |
1 |
4 |
5 |
6 |
8 |
10 |
500 |
|
2 |
6 |
4 |
3 |
5 |
8 |
500 |
|
|
3 |
9 |
7 |
4 |
2 |
4 |
500 |
|
|
Cпрос pi |
80 |
270 |
250 |
160 |
180 |
||
Решив задачу способом [2–4], определим оптимальный план.
Для решения данной задачи оптимизации на Python используется библиотека Pyomo.
1. Установка библиотеки Pyomo
Перед началом работы необходимо установить библиотеку Pyomo. Это можно сделать с помощью pip, выполнив следующую команду:
pip install pyomo
2. Импортирование необходимых модулей
Далее, импортируеются необходимые модули из библиотеки Pyomo:
from pyomo.environ import *
3. Определение данных
Сначала определяются данные для этой задачи оптимизации. В данном случае это матрица транспортных расходов (c), потребности покупателей (p) и производственные мощности предприятий (M).
# Определение данных
c = [[4, 5, 6, 8, 10],
[6, 4, 3, 5, 8],
[9, 7, 4, 2, 4]]
p = [80, 270, 250, 160, 180]
M = [500, 500, 500]
4. Создание модели
Далее, создается модель, используя функцию ConcreteModel() из модуля pyomo.environ. Модель состоит из переменных, целевой функции и ограничений.
# Создание модели
model = ConcreteModel()
# Определение множеств
model.I = RangeSet(5)
model.J = RangeSet(3)
# Определение переменных решения
model.x = Var(model.I, model.J, within= NonNegativeReals)
# Определение целевой функции
model.obj = Objective(expr=sum(c[i][j] * model.x[i,j] for i in model.I for j in model.J), sense=minimize)
# Определение ограничений
model.demand = ConstraintList()
for i in model.I:
model.demand.add(sum(model.x[i,j] for j in model.J) == p[i-1])
model.supply = ConstraintList()
for j in model.J:
model.supply.add(sum(model.x[i,j] for i in model.I) <= M[j-1])
В этом коде создается модель и определяются множества I и J, переменные решения x, целевую функцию obj и ограничения demand и supply.
5. Решение задачи оптимизации
Для решения задачи оптимизации используется стандартный солвер GLPK, который можно установить через pip. Далее вызывается метод solve() данной модели, который выполняет оптимизацию.
# Решение задачи оптимизации
SolverFactory(‘glpk’).solve(model)
# Вывод результатов
print(f»Минимальная стоимость доставки: {model.obj():.2f}»)
print(«\nР
Код программы для решения задачи линейного программирования с помощью Pyomo [5, с. 223]:
from pyomo.environ import *
# Создание модели
model = ConcreteModel()
# Определение множества I и J
I = [1, 2, 3, 4, 5]
J = [1, 2, 3]
# Определение параметров модели
M = {1: 500, 2: 500, 3: 500} # производственная мощность
p = {1: 80, 2: 270, 3: 250, 4: 160, 5: 180} # потребности покупателей
c = {(1, 1): 4, (1, 2): 5, (1, 3): 6, (1, 4): 8, (1, 5): 10,
(2, 1): 6, (2, 2): 4, (2, 3): 3, (2, 4): 5, (2, 5): 8,
(3, 1): 9, (3, 2): 7, (3, 3): 4, (3, 4): 2, (3, 5): 4} # транспортные расходы
# Определяются переменные решения
model.x = Var(I, J, within=NonNegativeReals)
# Определяется целевая функция
model.obj = Objective(expr=sum(c[i, j] * model.x[i, j] for i in I for j in J),
sense=minimize)
# Определяются ограничения на потребности покупателей
model.demand = ConstraintList()
for i in I:
model.demand.add(sum(model.x[i, j] for j in J) == p[i])
# Определяются ограничения на производственную мощность
model.capacity = ConstraintList()
for j in J:
model.capacity.add(sum(model.x[i, j] for i in I) <= M[j])
# Решается задача
solver = SolverFactory(‘glpk’)
solver.solve(model)
# Вывод результата
print(f”Optimal value: {model.obj():.2f}”)
print(“Solution:”)
for i in I:
for j in J:
print(f”x[{i}, {j}] = {model.x[i, j]():.2f}”)
Примечание. Для запуска данного кода необходимо установить Pyomo и выбрать один из доступных решателей (например, GLPK). При запуске программы получаем следующий ответ: 3350.00.
Заключение
Итак, существуют три библиотеки на Python, с помощью которых можно решить задачи линейного программирования: SiPy, Pulp, Pyomo. Значение целевой функции при использовании библиотеки Pyomo L(x) = 3350. При решении оптимизационных задач можете использовать библиотеку Pyomo.

