Для описания и анализа термомеханических свойств кристаллических тел применяют континуальные модели и модели, учитывающие дискретное строение вещества, состоящего из отдельных частиц (молекул, атомов, ионов) [1, с. 7]. В последнем случае нередко используют модель одномерного кристалла, которая позволяет провести относительно простые расчеты и визуализировать их результаты в наглядной форме [2, 3]. В этой модели частицы вещества располагаются на одной прямой и совершают перемещения вдоль этой прямой относительно положений равновесия.
Силы межатомного взаимодействия зависят от расстояния между частицами и рассчитываются различными способами. При малых отклонениях атомов от положений равновесия можно считать, что силы, действующие между ними, являются квазиупругими, а зависимость потенциальной энергии частицы от ее смещения из положения равновесия описывается квадратичной функцией (гармоническое приближение). С помощью модели гармонического приближения можно исследовать колебания атомов в кристалле, рассчитать теплоемкость кристаллической решетки, но рассмотреть тепловое расширение тел и явление теплопроводности эта модель не позволяет. Причиной теплового расширения твердых тел считают ангармонические колебания атомов [4].
Столкновения атомов (молекул, электронов, ионов) подразделяются на упругие и неупругие. Многие исследования проведены с учетом упругих столкновений атомных частиц [5, 6]. До настоящего времени в модели гармонических колебаний атомы рассматриваются как материальные точки, связанные друг с другом силами упругости. Возможность столкновений (соударений) атомов в этой модели не изучалась.
Цель и метод расчета
В данной работе сопоставлены два варианта одномерной модели кристалла: а) частицы вещества являются материальными точками, соударений между атомами нет; б) размеры атомов сопоставимы с расстояниями между их положениями равновесия, при сближении атомы абсолютно упруго сталкиваются.
Сила упругости между двумя ближайшими атомами рассчитывается:
Fx = kупр (xi – xi-1 – d),
где kупр – жесткость упругой связи; xi и xi-1 – координаты центров масс атомов; d – размер (условный диаметр) атома.
Выполнено компьютерное моделирование взаимодействия и перемещения атомов. Для расчета координат и скоростей частиц использован скоростной алгоритм Верле, применяемый в моделировании методом молекулярной динамики [7]. Исходными данными для расчетов являются: число атомов n, начальные координаты частиц x0i, проекции начальных скоростей v0i, коэффициент упругости kупр, размер d и масса атома m, число итераций расчета N. Время в процессе движения частиц изменяется дискретно с некоторым шагом Δt. В целях уменьшения погрешности расчетов при движении атомов в течение относительно большого времени NΔt шаг Δt выбирался таким, чтобы в процессе расчета энергия всей системы отклонялась от первоначального значения не более чем на 0,1%. На каждом шаге расчета определялись ускорения, координаты и скорости частиц. В момент времени t на атом с номером i действуют силы со стороны ближайших атомов с номерами i – 1 и i + 1. Ускорение этого атома:
ax(t) = Fsx(t) / m,
где Fsx(t) – сумма проекций сил действия двух ближайших частиц. Удаленные атомы на рассматриваемую частицу в данной модели не влияют.
Координата частицы в момент времени t + Δt:
x (t + Δt) = x (t) + vx(t) Δt + ax(t) Δt2/2.
Скорость частицы в этот же момент:
vx(t + Δt) = vx(t) + (ax(t) + ax(t + Δt))Δt/2.
Рассчитывались: средние значения координат частиц за время NΔt, отклонение средних координат от начальных, средние расстояния между ближайшими атомами в процессе их движения. Расчеты проведены для числа атомов от 3 до 30. Начальные положения частиц совпадали с их положениями равновесия (Fsx=0). В ряде расчетов начальные скорости атомов принимались одинаковыми по модулю. В большинстве случаев проекции скоростей всех частиц выбирались случайным образом из интервала [−vmax, vmax], но так, чтобы суммарный импульс системы был равен нулю.
Расчет коэффициента упругости силы взаимодействия между двумя атомами произведен на основании фрагмента потенциала Леннарда–Джонса (6–12). В этом потенциале на расстоянии σ между центрами атомов энергия их взаимодействия равна нулю. Минимум потенциальной энергии взаимодействия находится на расстоянии rmin=21/6σ. Глубина потенциальной ямы равна ε. Фрагменту потенциала от σ до rmin поставлена в соответствие квадратичная функция потенциальной энергии упругого взаимодействия
Ep = kупр Δl 2/2,
где Δl = rmin – σ, а Ep = ε.
Коэффициент упругости рассчитывается в этом случае:
kупр = 2ε / (rmin – σ)2.
Обширная информация о параметрах потенциала Леннарда–Джонса приведена в справочнике [8, с. 579]. Значения параметра σ для различных веществ в справочнике находятся в пределах от 0,2551 нм (гелий) до 0,6464 нм (2,2-диметилпропан). Отношение ε/k (где k – постоянная Больцмана) имеет значения от 10,22 K (гелий) до 809,1 K (вода). Рассчитанные для некоторых веществ коэффициенты упругости приведены в таблице.
В целях представления результатов расчета с наибольшей наглядностью в данной работе приняты следующие параметры: d=rmin=1 нм; kупр=10 Н/м; масса частицы (атома, молекулы) m=10 –25 кг; Δt=5.10 –15 с; N=10000.
Коэффициенты упругости для некоторых веществ
|
Вещество |
kупр, Н/м |
|
Гелий |
0,29 |
|
Метан |
1,94 |
|
Бензол |
2,65 |
|
Вода |
21,35 |
Результаты расчетов
На рисунке 1 изображены траектории движения шести частиц, полученные при следующих условиях расчета: v0x= ± 500 м/с (модули начальных скоростей одинаковы); атомы не соударяются. На рисунке 2 приведены результаты расчета параметров движения частиц при тех же начальных скоростях, но с учетом соударений. В этом случае, если xi – xi-1 – d < 0, то атомы с номерами i – 1 и i обмениваются импульсами, т.е. соударяются.
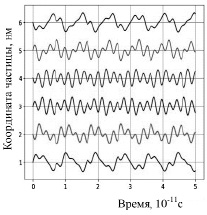
Рис. 1. Изменение координат частиц без соударений
Траектории движения частиц, представленные на рисунках 1 и 2, соответствуют ангармоническим колебаниям. При отсутствии столкновений (рис. 1) амплитуды колебаний больше, колебания происходят относительно начальных положений равновесия. В случае соударений объемных частиц амплитуды колебаний с течением времени (в пределах рассматриваемого временного интервала) уменьшаются, средние расстояния между атомами увеличиваются. Такое движение частиц можно считать колебаниями с ограничением амплитуды [9].
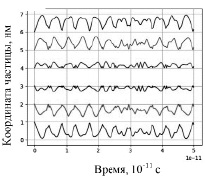
Рис. 2. Изменение координат частиц с соударениями
Расчеты показали: в случае учета соударений атомов, если их начальные скорости увеличиваются, то увеличиваются и средние расстояния между атомами (рис. 3). В случае отсутствия ударов между частицами средние значения координат совпадают с начальными координатами даже при значительном увеличении начальных скоростей частиц.
Колебания атомов в рассматриваемой модели являются ангармоническими (рис. 1 и 2). На любую частицу (кроме крайних на линии) в процессе ее движения действуют упругие силы со стороны двух ближайших атомов с одинаковыми коэффициентами упругости kупр. Но можно считать, что каждая частица перемещается под действием не двух, а одной суммарной (равнодействующей) силы, коэффициент упругости kvar которой является переменным. В этом случае любой атом перемещается под действием своей, индивидуальной квазипружины, а энергия атома в каждый момент времени складывается из его кинетической энергии и потенциальной энергии квазипружины:
Ep = kvarΔx2/2,
где Δx – смещение частицы от положения равновесия (деформация квазипружины).
На рисунке 4 приведена зависимость проекции суммарной силы от Δx для атома с начальной координатой 3 нм (без соударений, рис. 1). Для гармонического осциллятора (с постоянным коэффициентом упругости k) зависимость силы упругости от Δx имеет вид прямой линии, проходящей через начало координат: Fупр,x=− kΔx.
В описываемых расчетах все частицы в начальный момент времени находятся в положениях равновесия, т.е. начальные потенциальные энергии квазипружин равны нулю.
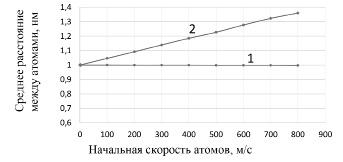
Рис. 3. Зависимость расстояния между атомами от их начальной скорости: 1 – без соударений; 2 – с учетом соударений
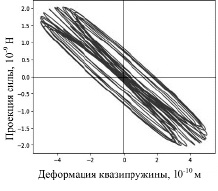
Рис. 4. Зависимость проекции суммарной силы от Δx
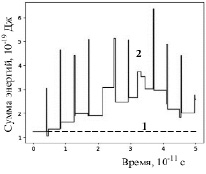
Рис. 5. Суммарная энергия частицы с начальной координатой 3 нм без соударений (1) и при наличии соударений (2)
Потенциальную энергию каждой квазипружины в некоторый момент времени можно рассчитать на основании теоремы о потенциальной энергии (как сумму работ за время NΔt, совершаемых консервативными силами на каждом временном интервале Δt).
В процессе движения и взаимодействия частиц их кинетические и потенциальные энергии меняются, между частицами осуществляется перераспределение энергий. Но этот процесс происходит различным образом при отсутствии и наличии соударений между частицами. Если соударений нет, то сумма кинетической и потенциальной энергий любой частицы в процессе ее движения остается постоянной: линия 1 на рисунке 5. В процессе соударений эта сумма претерпевает значительные изменения (рис. 5, линия 2).
Заключение
Рассмотрена одномерная модель твердого тела – цепочка одинаковых частиц (атомов, молекул, ионов), связанных квазиупругими короткодействующими силами. Выполнено компьютерное моделирование процессов взаимодействия и перемещения частиц в этой системе в двух вариантах: атомы рассматриваются как материальные точки, соударений между атомами нет (1); атомы имеют размеры сопоставимые с расстояниями между их центрами масс, при сближении соударяются (2).
В результате проведения расчетов выявлено, что колебания частиц в обоих случаях являются ангармоническими. Амплитуды колебаний материальных точек превышают амплитуды колебаний объемных атомов (при одинаковых условиях расчета). Колебания соударяющихся объемных атомов являются колебаниями с ограниченными амплитудами. Средние расстояния между материальными точками не меняются при изменении их скоростей, задаваемых в начале расчета, и равны начальным средним расстояниям. При увеличении начальных скоростей соударяющихся объемных частиц (при нагревании вещества) средние расстояния между атомами в процессе колебаний увеличиваются (вещество увеличивает свой объем).
Движение частицы, происходящее под воздействием упругих сил ближайших атомов, представлено как движение на квазипружине с переменным коэффициентом упругости. Рассчитана энергия каждой частицы как сумма ее кинетической энергии и потенциальной энергии квазипружины. В отсутствие соударений суммарная энергия частицы равна начальной в течение всего процесса движения. При соударениях суммарная энергия частицы претерпевает значительные изменения.
Полученные результаты могут быть полезны в исследованиях теплового расширения тел методом молекулярной динамики. В расчетных исследованиях теплового расширения необходимо учитывать вероятность того, что между молекулами (атомами) существуют взаимодействия, характеризуемые как соударения.

