К настоящему времени проведено большое число теоретических, экспериментальных и численных исследований особенностей тепло- и массопереноса в однокомпонентных сверхкритических флюидах вблизи критической точки. Выявлен ряд особенностей конвективного теплообмена, тепло- и массопереноса при нагревании границ замкнутой области (так называемый «пистон-эффект») и релаксации возмущений термодинамических параметров [1–3]. Характер обнаруженных особенностей существенным образом зависит от степени приближения к критической точке.
Можно ожидать, что в однородной по составу бинарной смеси должны проявляться все особенности тепло- и массопереноса, характерные для однокомпонентных флюидов. В самом деле, составленная в определенной пропорции из двух компонентов смесь может рассматриваться как некоторый новый однокомпонентный флюид. Критические параметры, термодинамические свойства и свойства переноса такого флюида могут быть найдены по известным свойствам составляющих. Этому вопросу посвящено множество исследований [4, 5], в которых предложены адекватные уравнения состояния для описания смеси с любым соотношением компонентов для большинства имеющих практическое значение смесей. Релаксация температурно-плотностной неоднородности в этом случае может быть описана с помощью уравнений, справедливых для описания однокомпонентной среды, и использования уравнения состояния для смеси.
В случае неоднородных по составу смесей система уравнений должна быть дополнена уравнением диффузии, а давление в бинарной системе представляется как сумма давлений компонентов.
В данной работе приведена система уравнений для расчетов движения и теплопереноса в бинарных смесях и представлен численный расчет релаксации неоднородностей плотности и температуры в однородной и неоднородной по составу смеси углекислого газа и шестифтористой серы, находящейся вблизи критической точки. В качестве температурно-плотностной неоднородности рассмотрен начальный разрыв температуры и плотности.
Целью исследования является определение особенностей тепло- и массопереноса в сверхкритических бинарных смесях.
Материалы и методы исследования
Исследование проводится методом численного решения системы уравнений для описания движения и теплопереноса в бинарной смеси.
Система одномерных безразмерных уравнений для описания движения и теплопереноса в бинарной смеси может быть записана в виде (прямым шрифтом изображаются безразмерные величины, а наклонным – размерные) [6]:
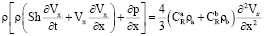 , (1)
, (1)
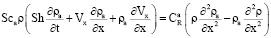 , (2)
, (2)
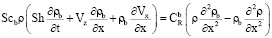 , (3)
, (3)
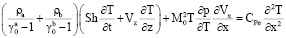 , (4)
, (4)
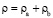 . (5)
. (5)
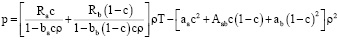 (6)
(6)
где 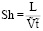 – число Струхала для смеси, L – масштаб длины,
– число Струхала для смеси, L – масштаб длины, 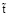 – масштаб времени, Ṽ – масштаб скорости;
– масштаб времени, Ṽ – масштаб скорости; 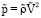 – масштаб давления,
– масштаб давления, 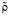 – масштаб плотности,
– масштаб плотности, 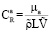 ,
, 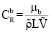 ,
, 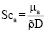 – число Шмидта для газа (a);
– число Шмидта для газа (a); 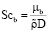 – число Шмидта для газа (b); D – коэффициент диффузии,
– число Шмидта для газа (b); D – коэффициент диффузии, 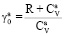 , R – универсальная газовая постоянная;
, R – универсальная газовая постоянная; 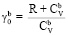 ;
; 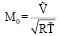 ,
, 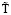 – масштаб температуры;
– масштаб температуры; 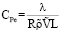 .
.
Здесь для t > 0, и 0 < x < 1 уравнение (1) является уравнением движения Навье – Стокса смеси газов (a) и (b) со скоростью Vx, уравнения (2), (3) представляют собой уравнения диффузии соответственно компонентов (а) и (b), уравнение (4) есть уравнение баланса энергии, соотношение (5) определяет плотность смеси как сумму плотностей компонентов (a) и (b) и уравнение (6) является уравнением состояния смеси (закон Дальтона).
В системе уравнений (1)–(6) ρ есть плотность смеси, p – давление смеси, D – коэффициент диффузии, T – температура смеси, λ – коэффициент теплопроводности. Отношение c = ρa / ρ является массовой концентрацией компонента (a), соответственно (1 – c) = ρb / ρ – массовая концентрация компонента (b).
При выводе системы уравнений предполагалось, что для динамической вязкости смеси μ и удельной теплоемкости смеси при постоянном объеме CV имеют место соотношения
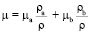 , (9)
, (9)
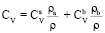 , (10)
, (10)
где μa, μb есть соответственно динамические вязкости компонентов (a) и (b), 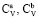 – соответственно удельные теплоемкости при постоянном объеме газов (a) и (b).
– соответственно удельные теплоемкости при постоянном объеме газов (a) и (b).
Уравнение состояния представляет собой сумму уравнений состояний компонентов (закон Дальтона) с поправкой Aabc(1 – c), учитывающей взаимодействие молекул компонентов (a) и (b) между собой [7].
Для вычисления безразмерных комплексов, входящих в уравнения (1)–(6), использовались следующие константы:
(CO2) Тс = 304,15 K, ρc = 470 кг/м3,
Ra = 188,95 дж/кг∙град, 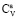 = 740 дж/кг∙град,
= 740 дж/кг∙град,
μa = 16∙10-6 Па∙с, 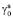 = 1,2553;
= 1,2553;
(SF6) Тс = 318,7 K, ρc = 744 кг/м3,
Rb = 56,9 дж/кг∙град, 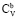 = 1000 дж/кг∙град,
= 1000 дж/кг∙град,
μb = 40∙106 Па∙с, 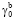 = 1,0569.
= 1,0569.
Значения коэффициента теплопроводности и коэффициента диффузии
λ = 1,2 вт/м∙град и D = 5∙10–8 м2/c.
Масштабы переменных L = 10–2 м,
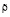 = 470 кг/м3,
= 470 кг/м3, 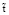 = 319 К,
= 319 К, 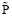 = 1,8 МПа,
= 1,8 МПа,
Ṽ = 49,17 м/c, 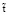 = L / Ṽ = 2,03∙10–4 c.
= L / Ṽ = 2,03∙10–4 c.
Представленная система одномерных безразмерных уравнений является модификацией системы уравнений для описания динамики и теплопереноса в однокомпонентной сверхкритической среде [8]. Вместо уравнения сохранения массы используются два уравнения диффузии компонентов, а уравнение состояния представлено в виде суммы уравнений состояний компонентов с поправкой, учитывающей взаимодействие молекул разных компонентов. Численная схема и методика расчетов сохранены в неизменном виде.
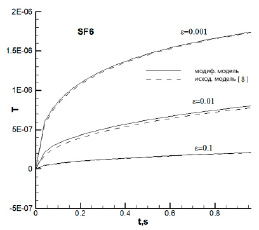
Рис. 1. Зависимость температуры в центре расчетной области от времени, рассчитанная по модифицированной (сплошная линия) и исходной [8] (пунктирная линия) модели
Исходная система уравнений использовалась в ряде работ авторов для расчетов пистон-эффекта и релаксации температурно-плотностных возмущений при нагревании границ замкнутого объема. Результаты расчетов показали хорошее согласие с экспериментом [8].
Для проверки правильности работы предлагаемой модификации модели было проведено сравнение расчетов с помощью модифицированной и исходной модели. Для сравнения был использован расчет нагрева замкнутой области, заполненной сверхкритической шестифтористой серой (SF6) в результате нагрева стенок [8]. На рис. 1 представлены графики зависимостей безразмерной температуры от времени в центре одномерной области при повышении температуры границ на 1 мК при различных значениях степени приближения к критической точке, характеризуемой величиной ϵ = (Т – Ткр.) / Ткр., где Ткр. – критическая температура. На рисунке видно хорошее согласие между кривыми, полученными с помощью модифицированной (сплошные кривые) и исходной (пунктирные кривые) модели.
Результаты исследования и их обсуждение
Расчеты релаксации начального разрыва температуры и плотности в одномерной области проводились для смеси углекислого газа (CO2), компонент (a), и шестифтористой серы (SF6), компонент (b). Границы области считались адиабатическими, а для скорости и плотности задавались условия непротекания.
Предполагалось, что в начальный момент времени в точке x = 0,1 (x – безразмерная координата) существует разрыв плотности и температуры. Cлева от поверхности разрыва (область (1)) среда имеет плотность ρ1, температуру T1, и концентрацию компонента (a) с1, а справа от поверхности разрыва (область (2)) плотность ρ2, температуру T2 и концентрацию компонента (a) с2. При этом значения плотности и температуры выбирались такими, что величина давления по обе стороны от разрыва одна и та же (p1 = p2). Расчеты проведены для случаев, когда в областях (1) и (2) в начальный момент состав смеси одинаков и когда в областях (1) и (2) находятся смеси разной концентрации c.
На рис. 2 представлен пример расчета зависимости распределения температуры и плотности для первого случая, когда в начальный момент времени область (1) и область (2) заполнены чистым CO2. В этом случае равенство давлений по обе стороны от поверхности разрыва можно обеспечить, только если ρ1 > ρ2, а T1 < T2. Из рисунка видно, что в этом примере с течением времени плотность справа от начального разрыва плавно растет, а слева плавно падает.
На рис. 3 представлен пример расчета распределения температуры и плотности для второго случая. В начальный момент времени в области (1) 0 < x < 0,1 находится смесь CO2 + SF6 с массовой концентрацией CO2 с = 0,995, а в области (2) 0,1< x < 1 находится чистый газ CO2 (с = 1). Плотность и температура в левой части области выше, чем в правой (ρ1 > ρ2 и T1 > T2 ).
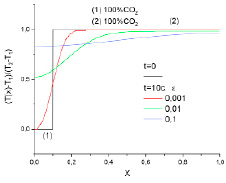
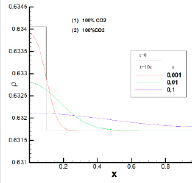
(а) (б)
Рис. 2. Распределение температуры (а) и плотности (б) для чистого CO2 (ρ1 > ρ2 и T1 < T2) в начальный момент и через 10 с в зависимости от степени приближения к критической точке ϵ = (Т – Ткр.) / Ткр.
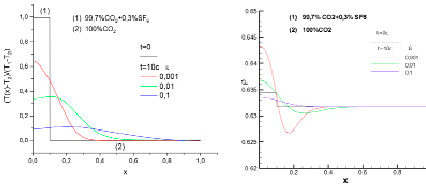
(а) (б)
Рис. 3. Распределение температуры (а) и плотности (б) для смеси 99,7 % CO2 + 0,3 % SF6 слева (область (1)) и чистого CO2 справа (область (2)) от поверхности разрыва (ρ1 > ρ2 и T1 > T2 ) в начальный момент и через 10 с в зависимости от степени приближения к критической точке ϵ = (Т – Ткр.) / Ткр.
Тем не менее величина давления слева и справа в начальный момент одна и та же (p1 = p2). Такое возможно только в случае, когда слева и справа от поверхности разрыва находятся смеси с разными молекулярными весами. Видно, что процесс релаксации начального распределения плотности при этом имеет существенные отличия от первого случая. Характерной особенностью здесь является образование локального уплотнения со стороны более плотной в начальный момент среды слева от поверхности разрыва и локального разряжения справа, где изначально плотность была меньше. Интенсивность эффекта увеличивается при приближении к критической точке.
Заключение
Проведено численное моделирование релаксации разрыва плотности и температуры при условии равенства начального давления по обе стороны от разрыва в однородной и неоднородной по составу сверхкритической бинарной смеси. В расчетах использовалась математическая модель, являющаяся модификацией системы уравнений для описания динамики и теплопереноса в однокомпонентной сверхкритической среде. Исходная модель была дополнена двумя уравнениями диффузии компонентов, а в качестве уравнения состояния использовалась сумма уравнений состояний компонентов с соответствующей поправкой, учитывающей взаимодействие молекул разных компонент. Пример расчета пистон-эффекта в однокомпонентной среде показал, что модифицированная и первоначальная модели дают сходные результаты. В случае неоднородной по составу бинарной смеси получено, что существует область параметров, в которой режим релаксации характеризуется значительными локальными изменениями плотности слева и справа от начального разрыва. Показано, что интенсивность локальных изменений плотности растет при приближении к критической точке.

