Интегральные уравнения Вольтерра очень широко применяются в задачах астрономии, биологии, экологии, электродинамики и механики [1]. С каждым днем все больше появляются новые области, где находят свои применения интегральные уравнения Вольтерра первого, второго и третьего родов. В работах А. Асанова, М. Иманалиева, С. Искандарова рассмотрены методы регуляризации, с помощью которых в теории интегральных уравнений Вольтерра первого и третьего родов доказывается существование и единственность решения [2, 3].
Интегральные уравнения Вольтерра первого рода являются некорректными задачами, и для их решения не могут быть применены стандартные методы, чтобы найти их решение, был использован метод приближенных решений, которые применяли в своих трудах В.О. Сергеев, Ж.А. Зулпукаров, Г.Б. Сапарова [4–6].
Материалы и методы исследования
В данной работе исследована система интегральных уравнений Вольтерра первого рода, в случае с двумя независимыми переменными, с помощью сингулярно-возмущенных уравнений методом регуляризации были доказаны существование и единственность решения данной системы.
Результаты исследования и их обсуждение
Рассматривается система
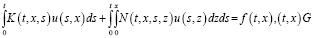 , (1)
, (1)
где K(t,x,s) и N(t,x,s,z) – (nхn) – матрицы функции, а u(t,x) – искомая и f(t,x) – заданная n – мерные вектор-функции на G = {(t,x): 0 ≤ t ≤ T, 0 ≤ x ≤ X}, f(0,x) = 0 при 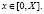
Введем норму, для nхn – матрицы A = (aij) следующим образом:
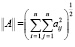 и для n–мерных векторов u = (u1,…,un) в виде
и для n–мерных векторов u = (u1,…,un) в виде 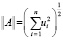 .
.
Введем переменную
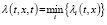 , (t,x)∈G, i = 1,2,…,n. (2)
, (t,x)∈G, i = 1,2,…,n. (2)
Потребуем выполнение следующих условий:
а) 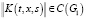 ,
, 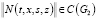 ,
, 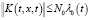 и
и 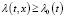 при (t,x)∈G, где N0 – const, λ(t,x) – определена с помощью формулы (2),
при (t,x)∈G, где N0 – const, λ(t,x) – определена с помощью формулы (2), 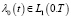 ;
;
б) при t > τ для любых (t,x,s),(τ,x,s)∈G1 = {(t,x,s): 0 ≤ s ≤ t ≤ T; 0 ≤ x ≤ X; } справедливо
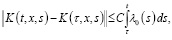
где 0<C – const;
в) при t > τ для любых (t,x,s,z),(τ,x,s,z)∈G2 = {(t,x,s,z): 0 ≤ s ≤ t ≤ T; 0 ≤ z ≤ x ≤ X} справедливо
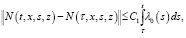
где 0 < C1 – const и N(t,x,t,z) ≡ 0 при (t,x,z)∈G4 = {(t,x,z): 0 ≤ t ≤ T; 0 ≤ z ≤ x ≤ X};
Наряду с системой (1) рассмотрим систему
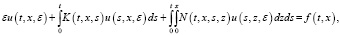 (3)
(3)
где 0 < ε – малый параметр.
Решение системы (3) будем искать в виде
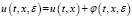 , (t,x)∈G. (4)
, (t,x)∈G. (4)
Подставляя (4) в (3), имеем
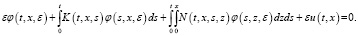 (5)
(5)
Из (5) получаем следующую систему:
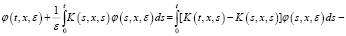
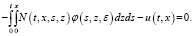 (6)
(6)
Резольвента матричного ядра 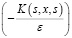 имеет вид
имеет вид
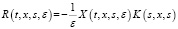 , ε > 0, (7)
, ε > 0, (7)
где X(t,x,y,s,ε) – матричная функция Коши системы 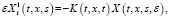
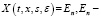 единичная матрица.
единичная матрица.
Отметим следующие свойства матричной функции X(t,x,s,ε):
10. 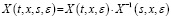 , (8)
, (8)
где X –1(t,x,y,ε) – обратная матрица матрицы X(t,x,y,ε)
20. 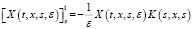 , (9)
, (9)
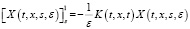 . (10)
. (10)
30. В силу неравенств Важевского и в силу условия а) имеет место
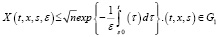 (11)
(11)
Далее, с помощью резольвенты R(t,x,y,s,ε),
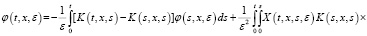
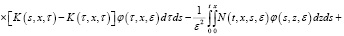
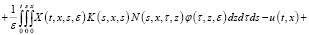
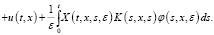
Используя формулу Дирихле и учитывая (9), (10), последнюю преобразуем к следующему виду:
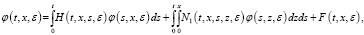 (12)
(12)
где 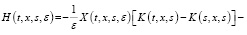
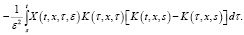 (13)
(13)
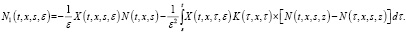 (14)
(14)
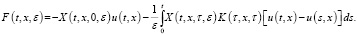 (15)
(15)
В дальнейшем используем следующие леммы.
Лемма 1. Пусть выполняются условия а), б), в) и г). Матричные функции H(t,x,s,ε), и N1(t,x,s,z,ε) определены соответственно с помощью формул (13) и (14). Тогда справедливы оценки
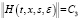 ,
, 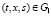 , ε > 0, (16)
, ε > 0, (16)
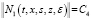 ,
, 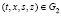 , ε > 0, (17)
, ε > 0, (17)
где 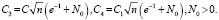
Доказательство. В силу условий а) – б) из (13) имеем
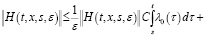
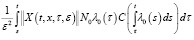 .
.
В этом случае в силу (11) для первого слагаемого имеем
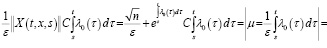
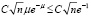 .
.
Для второго слагаемого справедливо соотношение
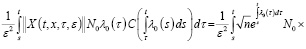
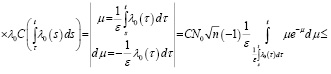
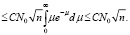
Следовательно, лемма 1 доказана.
Аналогично этому можно получить оценки (17).
Лемма 2. Пусть функция F(t,x,ε) определена формулой (15). Если u(t,x)∈Сn(G); u(0,x)=0 при x∈[0,X] и 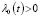 при почти всех t∈[0,T],
при почти всех t∈[0,T], 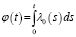 , t∈[0,T],
, t∈[0,T], 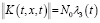 , то справедлива оценка
, то справедлива оценка
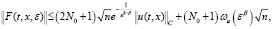 (18)
(18)
где β∈(0,1), 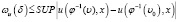 .
.
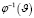 – обратная функция к
– обратная функция к 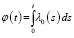 , т.е.
, т.е. 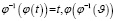 .
.
Доказательство. 1) Пусть 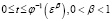 . Тогда из (18) имеем
. Тогда из (18) имеем
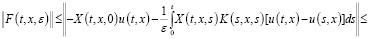
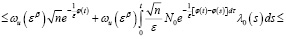
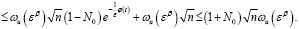 (19)
(19)
2) Если φ –1(εβ)≤ t ≤ Т, то
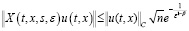 , (20)
, (20)
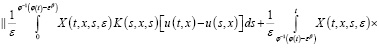
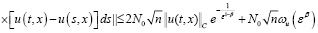 . (21)
. (21)
Учитывая (19), (20) и (21), из (15) получаем оценку (18).
Лемма 2 доказана.
В силу оценок (16), (17) и (18) из (12) получим
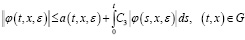 (22)
(22)
где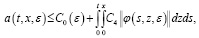 (23)
(23)
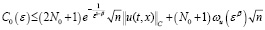 .
.
На основе леммы 1 неравенство (22) перепишем в следующем виде:
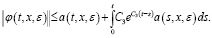
Вместо 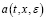 положим выражение (23) и из последнего неравенства имеем
положим выражение (23) и из последнего неравенства имеем
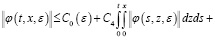
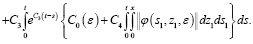
Это неравенство интегрируем и применим формулу Дирихле:
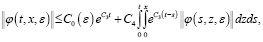
Затем, заменяя t на Т, получаем в виде
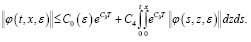 (24)
(24)
На последнюю (24) применим лемму 2, имеем
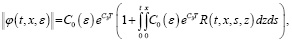
где 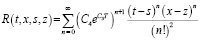 .
.
Из последнего уравнением имеем
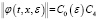 , (t,x,)∈G, (25)
, (t,x,)∈G, (25)
где 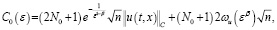
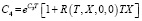 .
.
Таким образом, доказана следующая теорема.
Теорема 1. Пусть выполняются условия а), б), в) и система (1) имеет непрерывное решение 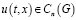 ,
, 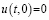 при x∈[0,X] и
при x∈[0,X] и 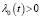 при почти всех t∈[0,T]. Тогда решение
при почти всех t∈[0,T]. Тогда решение 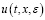 системы (3) при ε→0 сходится к непрерывному решению
системы (3) при ε→0 сходится к непрерывному решению 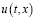 системы (1) в области G и справедлива оценка (25).
системы (1) в области G и справедлива оценка (25).
Теорема 2. Пусть выполняются условия а), б), в), г) и 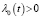 при почти всех
при почти всех 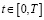 . Тогда решение системы (1) единственно в пространстве Сn(G).
. Тогда решение системы (1) единственно в пространстве Сn(G).
Доказательство. Пусть однородная система
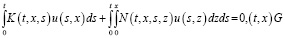
то есть система (1) при 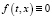 допускает ненулевое решение
допускает ненулевое решение 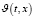 при (t,x)∈G. Последнюю систему перепишем в следующем виде:
при (t,x)∈G. Последнюю систему перепишем в следующем виде:
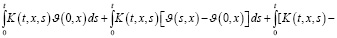
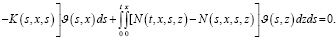 (26)
(26)
Обе части системы (26) скалярно умножаем на вектор 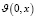 . Скалярное произведение обозначим символом
. Скалярное произведение обозначим символом 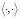 . Умножая справа и слева, затем суммируя их, имеем
. Умножая справа и слева, затем суммируя их, имеем
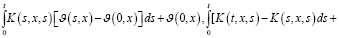
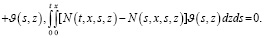 (27)
(27)
Отсюда, в силу условий теоремы, имеем
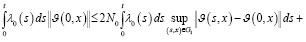
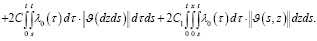 (28)
(28)
Далее, применяем формулу Дирихле и теорему о среднем и, деля обе части на 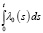 и переходя к пределу при t → 0, получим
и переходя к пределу при t → 0, получим
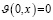 при x∈[0,X]. (29)
при x∈[0,X]. (29)
Из (1) при 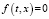 , (t,x)∈G, имеем
, (t,x)∈G, имеем 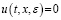 при всех (t,x)∈G, ε > 0. Тогда в силу теоремы 1 имеем
при всех (t,x)∈G, ε > 0. Тогда в силу теоремы 1 имеем
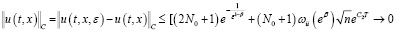
при ε→0. Таким образом 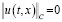 . Отсюда
. Отсюда 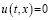 при всех (t,x)∈ G.
при всех (t,x)∈ G.
Теорема 2 доказана.

