Scientific journal

International Journal of Applied and fundamental research

ISSN 1996-3955

ИФ РИНЦ = 0,593

Введение

Под природой инерции понимается физический процесс, связанный с телом, благодаря которому явление инерции происходит и без которого оно бы не происходило. Природа инерции как сопротивления действию и природа движения по инерции трактуются как процесс, который состоит во взаимодействии тела со средой вакуумного пространства посредством поля инерции. Предполагается, что поле инерции тела состоит из таких же элементов, как поле гравитации [1; 2], но отличается незамкнутостью радиальных силовых линий. Состояние поля инерции тела в процессе текущего движения по инерции, после получения импульса, отличается от состояния этого поля в процессе предшествующего движения тела по инерции, до получения импульса, – в направлении и силе взаимодействия поля с элементами вакуума. Положение тела в пространстве рассматривается в координатах локальной системы отсчета, которая связана с центром гравитации системы, включающей тело. Предполагается [1–4], что вакуум состоит из таких же элементов, как поле инерции, но отличается их стохастической неупорядоченностью. В качестве предполагаемых элементов вакуума рассматриваются (е+е-)-пары «моря Дирака». При этом электрон и позитрон находятся в состоянии разделенных замкнутых вихрей, физически и пространственно связанных между собой. Как витки кругового тока они обращены друг к другу одноименными полюсами магнитных диполей, что исключает аннигиляцию. Предположения отличаются от аналогов из [1], а также [2; 3] и [4] тем, что постоянство круговых токов элементов (е+е-)-пары объясняется состоянием сверхпроводимости. Взаимодействие элементов пары, а также их взаимодействие с (е+е-)-парами вакуума определяется электромагнитными свойствами сверхпроводника, в числе которых статические и индукционные свойства. Индукционные свойства электрона и позитрона в состоянии сверхпроводимости проявляются аналогично эффекту Мейснера, подчиняются закону электромагнитной индукции Фарадея и правилу Ленца. В этих предположениях ставится задача описать закономерности инерции макроскопических тел как следствия взаимодействий элементов их полей инерции с элементами вакуумного пространства. В границах подхода постулируется сохранение фундаментальных физических закономерностей, принимается аксиома Лейбница: «истинно либо то, что с необходимостью следует из истины, либо то, что ничему истинному не противоречит».

Цель исследования – показать, как из предположения о сверхпроводимости элементов вакуума вытекают свойства инерции физических тел. Требуется раскрыть механизм взаимодействия элементов полей инерции и элементов вакуума, дать математическое обоснование подхода, указать возмущения орбитальных движений небесных тел, которые допустимо объяснять на основе предложенного подхода.

Исходные предположения о структуре вакуума, вещества и взаимодействии их элементов. Предположения опираются на прототипы из [1; 2], аналоги из [3; 4]. Принципиальное изменение состоит в гипотезе о сверхпроводимости элементов вакуума и компонентов нуклона, вытекающие отсюда следствия значительно отличаются от положений [1–4], что в деталях обсуждается в дальнейшем. Вводимые предположения созвучны гипотезе «моря Дирака», согласно которой вакуум состоит из соединенных в пары электронов и позитронов – (е+е-)-пар [5]. Современные представления о структуре вакуума опираются на эксперимент Жолио – Кюри, в котором электрон-позитронные пары порождаются из гамма–квантов в камере Вильсона в магнитном поле, разделяющем траектории электрона и позитрона [6]. Развитие представлений дают продолжающиеся эксперименты по появлению (е+е-)-пар из вакуума [7–10]. Выделяется эксперимент с графеновыми сверхрешетками, к которым ток подавался с силой, превышающей максимально возможную для вещества [11]. Графен выдержал ток, в процессе прохождения которого из вакуума в большом количестве появлялись электроны и позитроны, при этом они не аннигилировали. Необходимо отметить, что в работах Дирака и в их продолжение не объясняется, почему (е+е-)-пары в вакууме не аннигилируют, в какой мере и как эти элементы взаимодействуют между собой и с веществом, структура вакуума не детализируется. Ниже предпринимаются попытки трактовать классические представления о (е+е-)-парах, дополнив их предположениями о сверхпроводимости и индукционном взаимодействии. Это позволит объяснить устойчивость (е+е-)-пар в вакууме, их наличие и устойчивость в нуклонах атомных ядер, объяснить упругость вакуумного пространства. Основная цель работы – применить эти предположения для объяснения инертности и движения по инерции макроскопических тел. Конкретно используются следующие предположения из [1–4] с дополнениями в аспекте сверхпроводимости. Каждый элемент вакуума состоит из двух раздельных замкнутых тороидальных вихрей с круговыми осями. Один – свернувшийся в замкнутый вихрь электрон, другой – позитрон. Как замкнутый электрический вихрь, электрон (позитрон) предполагает свойства кругового витка постоянного электрического тока. Поскольку этот ток является постоянным и устойчивым, это означает состояние сверхпроводимости. Электрон имеет единичный заряд е-, как виток постоянного тока является магнитным диполем с полюсами N и S. Позитрон имеет единичный заряд е+, образует магнитный диполь с полюсами S и N. Механическое вращение материи обоих элементов пары имеет одинаковое направление, поэтому электрические токи являются противоположно направленными, обращенные друг к другу магнитные полюса – одноименными (условно – это полюса S). Как следствие, электрон и позитрон в паре взаимно отталкиваются и не аннигилируют. Окружности осей вращения электрона и позитрона в паре располагаются в параллельных плоскостях, их магнитные диполи образуют комбинацию полюсов NSSN. Внешний полюс пары всегда постоянен, предполагается, что это полюс N (если бы допускалась комбинация с внешним полюсом S, такие пары бы аннигилировали, что исключено). Винтовые шаги вихревых витков механического вращения пространственно ориентированы противоположно (рис. 1), что также препятствует аннигиляции. Соседние вихревые витки вращения вокруг круговой оси взаимно притягиваются, создавая силу центростремительного сжатия. Поэтому электрон-позитронная пара (кратко ±пара) имеет крайне малый диаметр круговой оси.

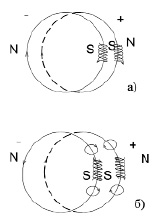
Рис. 1. Расположение магнитных полюсов в ±паре, винтовая (а) и электрическая (б) ориентация вихревых витков

В макроскопическом измерении ±пара имеет точечный размер. В ее объеме заключены два противоположных электрических заряда и две пары противоположных магнитных полюсов в состоянии взаимного отталкивания. Поэтому ±пара нейтральна относительно стационарных внешних зарядов и стационарного магнитного поля макроскопических тел и сама по себе не создает действия на макроскопические заряды и магнитные полюса. Вакуумное пространство, регистрируемое приборами, на которые множество ±пар не действует, по этой причине воспринимается как «абсолютная пустота». Однако макроскопические заряды и магнитные поля ориентируют ±пары. Вводится предположение, что электрон и позитрон в ±паре, как замкнутые электрические токи (круговые контуры), обладают свойством электромагнитной индукции, которая подчиняется правилу Ленца. Индукция не является непосредственным аналогом электромагнитной индукции, открытой Фарадеем для металлических проводников. Как круговой контур в состоянии сверхпроводимости, электрон (позитрон) в полной мере проявляет эффект Мейснера со всеми особенностями и свойствами, известными для некомпозитного проводника в состоянии сверхпроводимости. Соединения электронов и позитронов в пары замкнутых вихрей могли возникнуть в момент большого взрыва при зарождении вселенной (взрыв бинарной сверхплотной жидкости, сконцентрированной в одной точке). При этом вихри, в которых оказались обращенными друг к другу разноименные магнитные полюса, аннигилировали. Сохранились те, и только те пары вихрей, в которых под сверхвысоким давлением (что отвечало условиям создания сверхпроводимости) оказались обращенными друг к другу одноименные магнитные полюса. Где бы ни находилась такая ±пара, в силу крайне малого своего размера каждый контур пары будет вести себя как в вакуумной среде, что обуславливает сохранение сверхпроводимости: вакуум не оказывает сопротивление постоянному току. Пара сохраняет устойчивое состояние относительно центра симметрии. Ее противоположные электрические заряды притягиваются, противоположные токи создают магнитные диполи, направленные друг к другу одноименными полюсами, что препятствует сближению. Вследствие электромагнитной индукции эти поля при динамическом изменении расстояния между диполями индуцируют на обращенных друг к другу поверхностях электрона и позитрона вихревые токи, взаимное действие которых направлено против возникшего изменения магнитного потока. В случае сближения контуров в паре вихревые токи отталкивают их друг от друга, в случае взаимного отдаления вихревые токи меняют взаимное направление и притягивают их друг к другу. В результате электрон и позитрон в ±паре остаются на неизменном друг от друга расстоянии. Если на время рассуждения представить электрон (позитрон) ±пары в увеличенном масштабе до размеров макроскопического контура, то предполагаемые индукционные свойства составили бы набор известных индукционных свойств некомпозитного сверхпроводника [12; 13]. Приводимые ниже явления электромагнитной индукции в сверхпроводниках в преобразованном виде проецируются на контуры в ±парах (рис. 1).

Предположения об индукционных свойствах и эффекте Мейснера в ±парах, представление вакуума как ±среды. Во избежание терминологических оговорок термин «магнитный поток» сохраняется для магнитного поля в вакууме (общепринят термин «напряженность»). Обзоры исследований в области сверхпроводимости приводятся, в частности, в [13–15]. Экспериментальная демонстрация эффекта Мейснера в сверхпроводниках представлена в [16; 17], а также в [18; 19]. Ниже перечисляются проявления эффекта Мейснера, аналоги которых предполагаются свойствами электрона и позитрона ±пары.

1. Сразу при появлении внешнего магнитного поля на поверхности сверхпроводника (на поверхности контура ±пары) возникает вихревой ток, создающий свое собственное магнитное поле, направленное, по правилу Ленца, навстречу внешнему магнитному полю (при этом полное поле во внутреннем объеме проводника будет равно нулю).

1а. Индукционное сопротивление вихревых токов возникает при каждом изменении магнитного потока, пронизывающего площадь контура ±пары независимо от причины, по которой изменяется магнитный поток. Согласно правилу Ленца, индукционный ток в замкнутом проводящем контуре имеет такое направление, что он ослабляет причину своего возникновения (иначе говоря, чтобы противодействовать изменению магнитного потока, индуцирующего эти вихревые токи). В частности, это явление возникает, если магнитный поток неоднородного магнитного поля с ускорением движется навстречу контуру ±пары, а также если контур ±пары ускоренно движется навстречу магнитному потоку.

2. Поверхностные вихревые токи постоянны во времени и не затухают в неизменяющемся магнитном поле, в частности это так в контурах электрона и позитрона ±пары.

3. В объеме сверхпроводника (в контурах ±пар) внешнее и собственное магнитные поля складываются так, что суммарное магнитное поле становится равным нулю, хотя слагаемые поля существуют совместно и действуют взаимно независимо.

3а. Возникновение эффектов со свойствами 1 – 3 связано с тем, что при внесении сверхпроводника в магнитное поле в нем возникают вихревые токи индукции, магнитное поле которых полностью компенсирует внешнее поле. При этом индуцированное магнитное поле само создает вихревые токи, направление которых противоположно токам индукции по направлению и равно по величине. В результате в объеме сверхпроводника отсутствует и магнитное поле, и ток. Известное свойство сверхпроводимости таково, что ток сверхпроводимости существует только на поверхности сверхпроводника, причем одновременно с вихревыми токами на той же поверхности. Именно такое совместное существование тока сверхпроводимости и вихревых токов предполагается в контурах ±пары.

3б. Вместе с тем существуют незатухающие вихревые токи внутри сверхпроводника, которые создают внутреннее магнитное поле, противоположно направленное внешнему по отношению к ним «вихревому» магнитному полю и компенсирующее его.

4. Эффект Мейснера наблюдается только в слабых полях. При увеличении магнитного потока до критической величины сверхпроводящее состояние разрушается.

5. Магнит, приближающийся к сверхпроводнику, «видит» магнит одинаковой полярности и точно такого же размера. Отталкиваясь от неподвижного сверхпроводника, магнит «всплывает» сам и продолжает «парить» до тех пор, пока внешние условия не выведут сверхпроводник из сверхпроводящей фазы. Эффект работает и наоборот – сверхпроводник может зависать под магнитом. Применительно к контуру ±пары предполагается, что «одинаковый размер» встречного магнитного потока и магнитного потока индукционного сопротивления обусловлен их взаимодействием исключительно внутри бесконечного цилиндра, диаметр которого соизмерим с диаметром контуров ±пар.

6. Вращающийся сверхпроводник генерирует магнитное поле, точно выровненное с осью вращения (магнитный «момент Лондона» применяется в сверхпроводящих гироскопах для определения их осей вращения). Рассматриваемый гипотетический сверхпроводник – электрон, аналогично, позитрон ±пары можно считать механически вращающимся. Магнитное поле, точно выровненное с осью его вращения, контур ±пары генерирует вдоль высоты бесконечного цилиндра, диаметр которого соизмерим с диаметром контура ±пары, а высота перпендикулярна плоскости кругового тока и проходит через его центр.

7. Эффект Мейснера экспериментально демонстрируется как отталкивание поверхностными вихревыми токами одноименного полюса магнита. Если же плоский диск проводника в состоянии сверхпроводимости приблизить к неподвижному постоянному магниту снизу и отпустить, то диск не упадет. Он останется притянутым на таком же расстоянии, на каком отталкивался от сверхпроводника при приближении к нему сверху [16]. Согласно экспериментам [17–19] вихревые токи сверхпроводника создают магнитное поле, которое ускоренно приближающийся магнит отталкивает, ускоренно удаляющийся – притягивает, независимо от направленного к нему полюса магнита (индукционный ток всегда препятствует причине своего возникновения).

8. Индукционное взаимодействие сохраняет положение диска сверхпроводника на одном и том же расстоянии от цепочки контактно соприкасающихся притянутых друг к другу постоянных магнитов, когда диск движется вдоль цепочки по инерции [20], что говорит о сверхскорости переходных индукционных процессов в сверхпроводниках.

8а. Эксперименты [17–20] означают, что при каждой смене полюсов магнитов, над которыми (под которыми) движется диск в состоянии сверхпроводимости, на его поверхности, независимо от постоянных токов сверхпроводимости, меняется направление вихревых токов, причем так быстро, что не создает видимых изменений в положении равномерно движущегося диска.

8б. Эффект п. 8а сохраняется при движении по инерции вдоль ленты Мебиуса, образованной соединениями постоянных магнитов, когда сверхпроводящий диск периодически меняет свое положение, оказываясь то сверху, то снизу под поверхностью ленты [19]. При этом сверхпроводник удерживается на неизменном расстоянии от ленты независимо от полярности проходимых им при равномерном движении встречных полюсов магнитов и независимо от характера взаимодействия, будь то отталкивание или притяжение.

9. Магнит, ускоренно удаляющийся от сверхпроводника, «видит» магнит противоположной полярности и точно такого же размера, равно как ускоренно приближающийся магнит «видит» магнит одинаковой полярности, причем независимо от скорости смены приближений и удалений.

10. Когда сверхпроводящий диск зависает над постоянным магнитом, затем получает импульс в направлении, перпендикулярном нормали к плоскости диска, он начинает равномерно колебаться вдоль перпендикуляра к нормали, не соскальзывая с магнита.

10а. Когда между всеми соседними магнитами, дискретно соединенными в прямолинейную цепочку, остается зазор в четверть длины магнита, сверхпроводящий диск, получивший механический импульс, слегка проваливается в каждый зазор, но, каждый раз выравниваясь, продолжает поступательное движение вперед.

10б. При этом, когда заканчивается горизонтальная цепочка магнитов, но небольшая ее часть свешивается вертикально вниз, сверхпроводящий диск соскользнет вдоль свешенной части цепочки, но не упадет, а вернется вдоль нее обратно наверх. Эти два эксперимента проявляют индукционное сопротивление гравитационному притяжению.

11. Если в экспериментах с движением по инерции сверхпроводящего диска вдоль цепочки постоянных магнитов диск приводился в наклонное положение, то он продолжал движение по инерции именно в таком неизменном наклонном положении [17–20].

В предположении, что индукционные свойства сверхпроводимости соответствуют свойствам элементов вакуума, ниже предпринимается анализ природы инертности и движения по инерции при механических взаимодействиях макроскопических тел. Вначале, с учетом индукционных свойств, корректируются отдельные предположения о ±парах и их структурированных множествах. Вращающиеся электрон и позитрон ±пары генерируют магнитные поля, точно выровненные с осями вращения. Отсюда контуры ±пары зависают друг напротив друга, не соскальзывая с линии центров, и остаются на неизменном друг от друга расстоянии вдоль перпендикуляра к плоскостям механического вращения. Электромагнитная индукция препятствует любому динамическому изменению взаимного расстояния как следующему из этого изменению взаимных магнитных потоков. Это влечет свойство создавать вихревые токи в контурах ±пар, такие, что они противодействуют всякому изменению связей структурированного множества ±пар. Если в результате внешнего действия плоскости вращения электрона и позитрона в ±паре примут наклон друг к другу, то наклон сохранится до нового внешнего воздействия. На поверхностях электрона и позитрона ±пары вихревые токи реагируют в соответствии с правилом Ленца на любые изменения внешнего магнитного потока и всегда направлены так, чтобы противодействовать причине своего возникновения. Объединение отмеченных свойств делает устойчивость ±пары «абсолютной» (при отсутствии сильного внешнего электромагнитного воздействия, разрушающего сверхпроводимость). Пара подобна конструкции из двух механически скрепленных круговых сверхпроводников с противоположным направлением токов. Вакуумное пространство рассматривается как среда (ниже ±среда), состоящая из ±пар с описанными свойствами, только из таких элементов и только с такими свойствами. В реальной среде находится множество известных и неизвестных элементов с разнообразными свойствами, от которых дальнейшие рассуждения абстрагируются. Стохастические процессы ±среды представляются как детерминированное среднестатистическое состояние элементов. Исключения, при необходимости, оговариваются.

Предположения о структуре атомов, поля гравитации, инерции и стационарных электромагнитных полей. Множество элементов ±среды взаимодействует с физическим телом через его поля, состоящие из таких же элементов – из ±пар. Гравитационное, электромагнитное и описываемое ниже поле инерции обладают силовыми линиями, которые образованы из ±пар, но различаются структурой связи элементов. Если множества элементов ±среды не принадлежат силовым линиям поля, то они не структурированы. Силовые линии каждого поля имеют структуру, с единственностью отвечающую разновидности поля. Искомая природа инерции состоит во взаимодействии тела с элементами ±среды, потребуется отличать состояния локального покоя и движения, указывать роль ±среды в различии этих состояний и в сопротивлении приложенной силе. С этой целью детализируется структура каждого из рассматриваемых полей. Предполагается, что силовые линии поля образуются благодаря тому, что нуклоны ядра атома состоят из ±пар, в нуклоне они соединены в сферическую структуру. Нейтрон – сферическая поверхность, покрытая ±парами, плоскости контуров которых расположены в параллельных касательным к поверхности плоскостях (рис. 2). Соседние ±пары чередуют сдвиг вдоль радиусов сферы, в соответствии сдвигам чередуют знак внешнего заряда в шахматном порядке. Этот порядок однократно нарушен, в месте нарушения образуется локальный избыток отрицательных зарядов, центральный из них выдавливается окрестными одноименными зарядами с поверхности, когда нейтрон оказывается в свободном состоянии. Тогда он излучает электрон и приобретает единичный положительный заряд сохранившегося в его структуре позитрона, образуя протон. В ядре атома это не происходит (если атом не радиоактивен): избыточная отрицательная зона нейтрона ориентирована на положительный заряд протона, образуя соединение, связывающее протоны и нейтроны в ядре. Дополнительная сила связи обусловлена тем, что позитрон в структуре протона имеет внешний магнитный полюс S, сохранившийся от ±пары после отделения электрона. Все другие внешние магнитные полюса ±пар нейтрона есть N. Пусть рассматривается нейтрон (рис. 2).

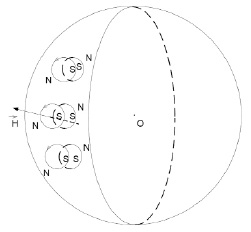
Рис. 2. Магнитная ориентация ±пар на сфере нейтрона

Перпендикулярные плоскостям контуров линии центров ±пар попарно повернуты друг относительно друга на ≈180º, чередуя на сфере заряды «+» и «–» в шахматном порядке:

(1)

Под каждым «+» из (1) на внутренней стороне сферы нейтрона располагается сдвоенный с ним «–», под каждым внешним «–» располагается сдвоенный с ним «+». Линии центров ±пары располагаются радиально к центру сферы. В таком положении ±пары удерживаются взаимным притяжением зарядов. Кроме того, ±пары чередуют смещение линий центров к центру нейтрона и обратно, усиливая взаимное притяжение за счет смещения внешних магнитных полюсов соседних ±пар к внутренним, им противоположным. Протон – следствие того, что чередование (1) на поверхности нейтрона однократно нарушено:

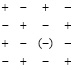(2)

Соседние отрицательные заряды выталкивают лишний «внутренний» между ними заряд (–), восстанавливая расположение (1). На поверхности остается не скомпенсированный позитрон с зарядом «+» в состоянии устойчивого замкнутого вихря. В результате нейтрон распадается на протон и электрон, протон остается с зарядом позитрона. Эта реакция известна как β-распад:

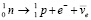
После распада протон становится «абсолютно» устойчивым. В ядре атома заряд протона «+» ориентируется на зону отрицательного участка поверхности нейтрона вокруг (–), как иллюстрирует (2). В совокупности это влечет особенности ядра, на основе которых объяснимо наличие электрона в ядре атома, равенство абсолютных величин зарядов протона и электрона, происхождение орбитальных электронов атома, равенство их количества числу протонов ядра в неионизированных атомах. Сравнительно наглядно объясняется естественная радиоактивность с излучением электронов (β--распад), а также сдвоенных протонов и нейтронов (α-частиц) вследствие сохранения в них взаимной ориентации зарядов на поверхности. Естественность процесса распада именно тяжелых ядер урана объясняется дефицитом локального пространства для взаимной ориентации нейтронов и протонов. Объяснимо также излучение позитронов (β+-распад) в явлениях искусственной радиоактивности, появление одновременно электронов и позитронов (β+ и β--распады) в процессе распада α-частиц (вырываются связанные взаимной ориентацией позитроны и электроны). Допускает объяснение механизм происхождения отрицательного заряда анти-альфа-частиц [6] и антипротонов. Можно предположить, что на момент зарождения ±пар в вакууме могли образоваться и более сложные их пространственные комбинации – атомы и молекулы. Из сверхпроводимости контуров ±пар и их индукционных свойств следует, что индукционность элементов в нуклонах атомных ядер, в орбитальных электронах атомов усиливает устойчивость стационарных связей в структурах нейтронов, протонов, атомных ядер, атомов и молекул. Ядро атома ориентирует ±пары из ±среды в своей окрестности. Ближайшая ±пара ориентируется зарядом ее электрона на заряд протона ядра либо внутренней парой магнитных полюсов S на внешний магнитный полюс N на сфере нуклона. Ориентированные ±пары в свою очередь ориентируют ближайшие к ним ±пары среды, и так – до образования силовой линии. Устойчивость силовых линий поддерживают индукционные взаимодействия элементов. Силовая линия гравитации отличается от силовых линий электрического и магнитного полей тем, что имеет неравномерно чередующуюся взаимную ориентацию зарядов ±пар и полюсов их магнитных диполей. Это не исключает суперпозиции магнитных диполей ее ±пар. В макроскопической окрестности центра тяжести тела силовые линии гравитации исходят из него как из центра симметрии. Каждая такая силовая линия имеет вид прямолинейной цепочки ориентированных друг на друга ±пар (в дальнейшем линейных ±пар), последовательное чередование зарядов которых прерывается перпендикулярно расположенными ±парами (в дальнейшем ортогональными ±парами). Ортогональные ±пары образуются за счет ориентации на внешний магнитный полюс N линейной пары одновременно двух внутренних полюсов N ортогональной ±пары. На этой основе образуется прямолинейная цепочка вида

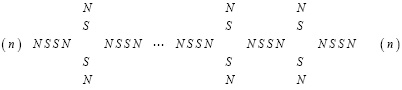, (3)

где в промежутке между ортогональными ±парами соседние линейные ±пары чередуют знак заряда на обращенных друг к другу концах:

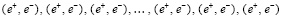. (4)

Длина цепочки (4) из линейных ±пар сравнительно невелика, в (3) она показана трижды состоящей всего из одной ±пары. Символ (n) в (3) означает, что цепочка от нуклона атома одного тела идет к нуклону атома другого тела, образуя между ними притяжение (силовая линия гравитации замкнута). Цепочка (4) в структуре (3) может иметь видоизменение:

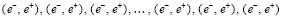. (5)

В этом случае две части цепочки линейных ±пар (4) и (5) расположены по разные стороны от ортогональной ±пары. Обращенность друг к другу одноименных зарядов по обе стороны от ортогональной ±пары не влечет отталкивание таких линейных ±пар друг от друга. Расстояние между этими одноименными зарядами вдвое больше расстояния между противоположными магнитными полюсами, при этом полюс N линейной ±пары притягивается сразу к двум полюсам S ортогональной ±пары, как в (3). Цепочка (3) изображена на плоскости, в пространстве ортогональная ±пара может расположиться с тем же центром симметрии произвольным образом в плоскости круга, перпендикулярного цепочке. Это влечет пространственные ответвления в перпендикулярном направлении. В свою очередь перпендикулярно к перпендикуляру ответвления может возникнуть цепочка, параллельная исходной цепочке. При этом комбинации (4), (5), будучи параллельными, взаимно притягиваются, что скрепляет силовую линию, придает ей объем, усиливает эффект ее нейтральности в макроскопическом пространстве. Тому же способствует взаимный сдвиг магнитных диполей и зарядов в параллельных цепочках. При этом сохраняется прямолинейность продольной оси силовой линии в целом. Устойчивость связей в структуре силовой линии усиливается индукционными взаимодействиями элементов. Изображение (3) – (5) принимается за условное обозначение взаимной ориентации элементов силовых линий атомов и физических тел. В реальности элементы подчиняются вероятностным закономерностям. В среднем принадлежащая силовой линии ±пара находится в положении, обозначенном в (3) – (5), с вероятностью P > 1/2. Силовая линия инерции (радиальная силовая линия) повторяет структуру силовой линии гравитации с тем принципиальным отличием, что не замыкается на другое тело, в ее изображении исключается второй символ (n):

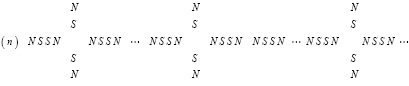(6)

Происхождение и особенности структуры будут детально обсуждаться в дальнейшем. Силовая линия, которая состоит только из цепочек вида (4) или (5), относится к электростатическому заряду, поле которого состоит из ориентированных таким образом линейных ±пар. Силовая линия стационарного магнитного поля состоит из элементов вида 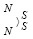, где предполагается, что прямолинейный отрезок линии центров контуров ±пары изогнут посередине под некоторым углом. Угол наклона к исходной линии центров должен быть много меньше прямого, иначе ±пара аннигилировала бы с ±парами ±среды вследствие взаимной обращенности разноименными магнитными полюсами. Изображение силовой линии стационарного магнитного поля представимо цепочкой

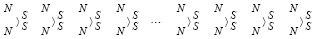. (7)

Такая изогнутость ±пар создает ориентацию стационарного магнита. Согласно предположениям, если внешним действием плоскость вращения элемента ±пары была приведена в наклонное положение, то элемент продолжает постоянно оставаться именно в таком неизменном наклонном положении. В положении (7) элементы ±пары могли оказаться под влиянием внешнего магнитного поля. В комбинации (4), (5) ±пары переводятся под влиянием стационарного электрического заряда тела. Структуры поддерживают взаимное соединение элементов в цепочках индукционным взаимодействием контуров ±пар. С учетом суперпозиции ориентированных зарядов и магнитных диполей достигается передача притяжения и отталкивания от элемента к элементу. Передача притяжения в силовых линиях инерции (6) достигается суперпозицией магнитных диполей линейных ±пар, всегда ориентированных во внешнем направлении полюсом N, притягивающихся вдоль прямой к двум полюсам S каждой из ортогональных ±пар, множество которых подчиняется своей отдельной суперпозиции. В любой передаче действия участвует индукционный процесс, поскольку притяжение или отталкивание – динамическое изменение взаимного положения и магнитного потока соседних ±пар, чему индукция противодействует. Поле инерции тела образуется из радиальных силовых линий (6), симметрично выходящих из центра тяжести. Такое поле существует у каждого тела, не зависит от поля гравитации, аналогично тому, как у одного и того же тела могут автономно существовать поле гравитации, электрическое и магнитное поле. Автономность каждого поля поддерживается индукционным противодействием изменению взаимного положения элементов.

Взаимодействие радиальной силовой линии и ±среды. Наряду с индукционными свойствами есть физическая, одновременно с тем геометрическая и вероятностная причина существования радиальных силовых линий, которая заключается в следующем. Пусть произвольно зафиксирована прямая линия в ±среде и зафиксирована линейная ±пара, линия центров которой лежит на этой прямой (именно такая ±пара ниже называется линейной). Внешний полюс N этой ±пары «видит» вдоль прямой одновременно два сдвоенных полюса S ортогональной ±пары, середина линии центров которой лежит на этой же прямой (именно такая ±пара ниже называется ортогональной). Ортогональная ±пара необходимо найдется на прямой (найдется их бесконечное множество). К ортогональной ±паре линейная ±пара притягивается. Одновременно линейные и одновременно ортогональные ±пары между собой взаимно отталкиваются. Полюс N линейной ±пары «видит» одновременно два противоположных полюса N и S у любой ±пары, которая не является линейной или ортогональной, в частности если середина ее линии центров не лежит на рассматриваемой прямой. Взаимодействие линейной ±пары с такими ±парами имеет более высокий порядок малости, чем взаимодействие с линейными и ортогональными ±парами. То же можно отнести к взаимодействию с ±парами ортогональной ±пары. На этом основании в дальнейшем учитывается взаимодействие только вдоль прямой, соединяющей середины линий центров, исключительно линейных и ортогональных ±пар. Их составное действие друг на друга образуется по принципу суперпозиции и является доминирующим по отношению к взаимодействиям более высокого порядка малости. Нестрогость этого рассуждения снижается в силу свойства п. 6: вращающийся сверхпроводник контура ±пары генерирует магнитное поле, точно выровненное с осью вращения – вдоль фиксированной прямой. Принципиально следующее. Вдоль прямой располагается множество точек середины линий центров ортогональных и линейных ±пар (рис. 3).

В силу равной вероятности всевозможных положений наибольшее их количество будет принадлежать ортогональным ±парам, середины линий центров которых совпадают с центрами кругов, перпендикулярных прямой (ибо на таком круге ортогональная ±пара может оказаться в любом из возможных положений, рис. 3). Ортогональные ±пары образуют на прямой множество большей мощности, чем множество линейных ±пар.

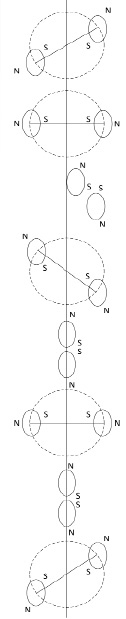
Рис. 3. Расположение на прямой в пространстве середины линий центров ±пар (окружности располагаются в плоскости перпендикулярной прямой)

Суперпозиция магнитного поля с полярностью S оказывается доминирующей на прямой, и полюс N линейной ±пары притягивается вдоль этой прямой к ортогональным ±парам. Линейная ±пара будет притягиваться с равной силой вдоль прямой в прямом и обратном направлении. Однако если прямая является продольной осью радиальной силовой линии тела, то притяжение линейной ±пары со стороны ортогональных ±пар будет происходить только в центробежном от тела направлении, поскольку, согласно (6), в любой конечной цепочке радиальной силовой линии число линейных ±пар в промежутках между соседними ортогональными ±парами превосходит число ортогональных ±пар. Их притяжение к бесконечному множеству ортогональных ±пар вдоль прямой будет превосходить взаимное отталкивание ортогональных ±пар. Поэтому вся радиальная силовая линия, а посредством нее и тело, притягивается со стороны ±среды в центробежном направлении. На ограниченной по длине радиальной силовой линии – избыток линейных ±пар, на ее бесконечном прямолинейном продолжении – избыток ортогональных ±пар. В результате создается пространственное притяжение всей радиальной силовой линии (и тела) в центробежном направлении. Именно такое прямолинейное притяжение формирует радиальные силовые линии и определяет качество их прямолинейности, отличающее их от замкнутых силовых линий гравитации. Из центра тяжести тела в одном направлении параллельно выходит несколько продольных осей линейных цепочек вида (6). Они взаимно сдвигаются так, что притягиваются друг к другу смежными полюсами магнитных диполей и противоположными электрическими зарядами, суммарно это усиливает притяжение в центробежном направлении вдоль продолжающих их прямых. Такая группа параллельных радиальных силовых линий в дальнейшем принимается за единую радиальную силовую линию. Она занимает внутренний объем цилиндра, основание которого проходит через центр тяжести тела, он имеет конечную высоту и будет называться радиальным цилиндром. Бесконечное продолжение этого цилиндра в центробежном направлении включает все полупрямые внешнего продолжения цепочек радиальной силовой линии. От начальной точки их продолжения (от конца высоты радиального цилиндра) цилиндр именуется полубесконечным цилиндром (бесконечным продолжением радиального цилиндра). Предполагается, что радиальный и полубесконечный цилиндры имеют «сколь угодно» малый в макроскопическом измерении, но фиксированный диаметр. Полубесконечный цилиндр состоит из стохастических ±пар, тогда как радиальный цилиндр состоит из ±пар в детерминированной структуре вида (6). В стационарном состоянии в силу симметрии на центр тяжести тела действует равная сила в любом радиальном направлении, поэтому притяжение тела со стороны всех элементов ±среды уравновешивается и в сумме равно нулю. Прямая, линейная и ортогональные ±пары на ней инвариантно строятся в любой точке ±среды. Линейная ±пара сама является ортогональной для любой прямой, перпендикулярно проходящей через середину ее линии центров. Поэтому каждая ±пара испытывает притяжение со стороны ±среды, как следствие, ±среда является упругой. В силу симметрии ±среда изотропна. Изотропная упругость поддерживается индукционностью элементов, препятствующей динамическому изменению положений соседних ±пар. Возможность пренебречь действием на линейную ±пару не ортогональной пары является эвристическим замечанием. Множество не учитываемых ±пар бесконечно. Сумма их действий на линейную ±пару может не равняться нулю. Поэтому возможность пренебречь их действием в дальнейшем принимается как формальное предположение.

Стационарное притяжение тела ±средой. Пусть рассматривается неподвижное однородное сферическое тело макроскопического размера массой m с центром тяжести o на поверхности Земли. Покой и движение тела, пока не оговорено иное, рассматриваются относительно точки o в фиксированных на поверхности декартовых координатах. Предполагается, что количество цепочек (6) в радиальном цилиндре зависит от массы тела и от расстояния до центра o, а количество радиальных силовых линий пропорционально m. Из [2] с модификацией заимствуется следующее предположение. Элемент стационарного действия – дифференциал модуля силы – однородного сферического тела единичной массы на сколь угодно малый в макроскопическом измерении элемент радиального цилиндра на расстоянии r от центра o может быть представлен в виде

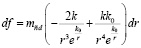. (8)

Здесь k = const, k0 = const – постоянные коэффициенты, значение которых неизвестно; mcd – масса ортогонального среза радиального цилиндра (кратко – среза), который имеет «сколь угодно» малую, но фиксированную толщину. Пока не оговорено иное, значение mcd полагается неопределенным. Умноженная на приращение dr, эта масса дает массу элемента радиального цилиндра. Элемент действия (8) имеет электромагнитную природу на уровне взаимодействия ±пар, в макроскопическом измерении выражает механическое действие. Полное действие тела единичной массы на элемент радиального цилиндра есть

.

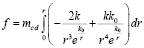Очевидно, ,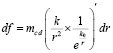

отсюда, в обозначении ,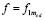

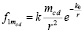, (9)

где единичный индекс 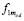соответствует единичной массе. Элемент радиального цилиндра также действует на тело единичной массы, причем с такой же силой, как в правой части (9). Это обратное действие не имело бы физического смысла (тело притягивается полем, которое само создает), если бы элементы радиальной силовой линии не притягивались элементами бесконечного продолжения радиального цилиндра. В данном случае элемент радиального цилиндра передает действие на тело и, имея опору со стороны элементов полубесконечного цилиндра, сам вносит в это действие вклад в виде силы (9). Если раскрыть выражение 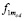, то (9) примет вид

,

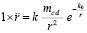где в записи 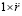выделена единичная масса тела. Обе части равенства можно умножить на m. В результате получится действие элемента радиальной силовой линии на тело массой m на расстоянии r от его центра тяжести:

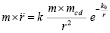
или в обозначении ,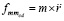

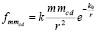. (10)

Соотношение (10) согласуется с тем, что число структурированных элементов радиальной силовой линии пропорционально m. Однако необходимо скорректировать соотношение, поскольку действие на тело с ростом r переходит в действие со стороны элементов полубесконечного цилиндра, элементы которого не структурированы, их действие на тело не связано с его массой. Понятие массы элемента вакуума в механике не определено. Если же это понятие не ввести, нельзя пользоваться законами динамики. Если это понятие оставить, как по умолчанию выше, оно не будет соответствовать рассеянию с расстоянием структуры силовой линии. Поэтому в качестве массы элемента радиальной силовой линии (с сохранением обозначения и термина) принимается масса множества структурированных ±пар в этом элементе, то есть тех, которые входят в структуру радиальной силовой линии (6). Тем самым учитываются массы тех и только тех ±пар, которые непосредственно участвуют в рассматриваемом взаимодействии. Замена mcd в (10) на массу второго тела M влечет

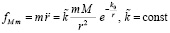[2; 3], –

аналог закона всемирного тяготения. Если же вместо (3) рассматривались бы цепочки (4), (5), получался бы аналог закона Кулона

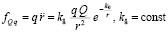[1; 3].

В этих аналогиях и в (10) требует пояснения множитель .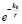

Во-первых, 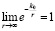, так что 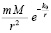эквивалентно 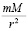с ростом r. При макроскопическом измерении r и при выборе соответственного k0 формально получается закон обратных квадратов.

Во-вторых, 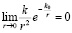, в результате исчезает дефект закона обратных квадратов, состоящий в том, что если любые точечные тела имеют конечные массы M ≠ 0, m ≠ 0, то на нулевом расстоянии между ними сила взаимодействия обращается в бесконечность, –

,

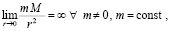
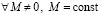что противоречит реальности.

В то же время

,

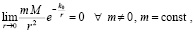
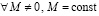что можно интерпретировать как переход от макроскопических расстояний к расстояниям микромира. Пусть снова, на время рассуждения, каждый элемент радиального цилиндра действует на тело массой m с силой (10). Тогда множество всех элементов радиального цилиндра и его бесконечного продолжения образует интегральную сумму действий на тело. Такое действие необходимо разделять на действие вдоль высоты радиального цилиндра, где сохраняется структура связи элементов (6), и на действие вдоль оси его бесконечного продолжения, где связь элементов является чисто стохастической. Структуры будет разделять граница Rm. Отрезок 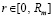соответствует структурированным элементам, его бесконечное продолжение 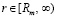– элементам стохастической структуры. Интегральная сумма действий на тело всех элементов радиального цилиндра составит

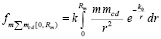, (11)

где индекс m соответствует телу массой m; индекс Σmcd соответствует всем взаимодействующим с этим телом элементам радиального цилиндра вдоль [0, Rm]. Взаимодействие является взаимным притяжением тела и элементов. Полупрямая, проходящая из центра o через продольную ось радиальной силовой линии, обозначается [o, ∞), иногда [0, ∞), как если бы она принадлежала оси абсцисс. Масса среза радиального цилиндра, mcd, на расстоянии r от центра o не является постоянной (по принятому определению учитывается масса множества структурированных ±пар), она убывает с ростом r вследствие «рассеяния» («разрушения») структуры силовой линии. В радиальном цилиндре с ростом r сохраняется все меньше элементов, имеющих структуру вида (6). В элементе силовой линии могут находиться ±пары, не структурированные в радиальную силовую линию, но они не включаются в численную меру рассматриваемой массы. Это убывание числа структурированных элементов означает, что масса mcd зависит от r. Предполагается, что

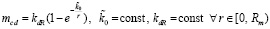, (12)

где 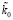, kdR – постоянные коэффициенты, значение которых неизвестно. Принимается, что в общем случае 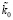не зависит от массы тела m, и, напротив, kdR пропорционально m, kdR = kR × m, kR = const, – но только на отрезке [0, Rm). Для соотношений (12) предполагается параллельность линий центров линейных ±пар в структуре радиального цилиндра. Отсюда радиальные силовые линии тела попарно отделены друг от друга на некоторый угол. Это определяет их рассеяние с удалением от тела. В бесконечном продолжении радиального цилиндра, вдоль [Rm, ∞), масса ортогонального среза mcd является константой, она определяется тем и только тем качеством, что в этом продолжении радиального цилиндра количество ортогональных ±пар с серединой линии центров на [Rm, ∞) существенно больше, чем линейных ±пар с таким же расположением середин линий центров. В итоге распределение (12) включается в следующее распределение массы ортогонального среза:

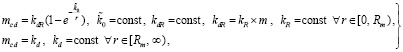(13)

где значение kd неизвестно (как неизвестно и значение kdR). Согласно (13) Rm таково, что при r = Rm значения mcd совпадут. Отсюда 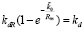, и .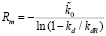

С поправкой на ограничение r ≤ Rm. оценка (11) модифицируется с подстановкой (13):

.

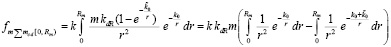Отсюда

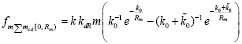. (14)

При r ≥ Rm соотношения (8) – (11) изменятся вследствие (13).

Действие 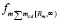на тело массой m примет вид

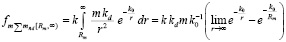
или 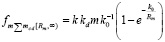. (15)

В результате, действие 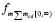притяжения тела массой m со стороны радиального цилиндра и его бесконечного продолжения оценивается как сумма

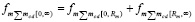, (16)

где 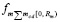из (14), 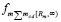из (15). Окончательно:

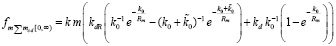. (17)

При этом 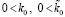, значения обоих слагаемых (16) положительны. Обе эти силы одинаково направлены на притяжение тела со стороны ±среды в центробежном от тела направлении вдоль [o, ∞). Пока тело неподвижно, вследствие стационарности полей контуров ±пар, они не меняются, их сумма постоянна:

.

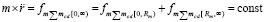Сила 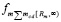приложена не непосредственно к центру тяжести тела, а притягивает элементы радиального цилиндра вдоль [0, Rm). Элементы радиального цилиндра, соответственно сила 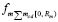, притягивают элементы полубесконечного цилиндра и тело вдоль [Rm, ∞).

Пусть перпендикулярно полупрямой [o, ∞) через центр тяжести тела o проведена плоскость. Полупространство, которому принадлежит эта полупрямая, определяется как правое полупространство, полуплоскость, содержащая полупрямую [o, ∞), – правая полуплоскость, полупрямая [o, ∞) – правая полупрямая. Противоположное полупространство определяется как левое полупространство, соответственно, левая полуплоскость, левая полупрямая [o, – ∞) до бесконечности продолжает полупрямую [o, ∞) в левом полупространстве. Разделяются также левый и правый радиальные цилиндры, левый и правый полубесконечные цилиндры. В обозначение сил (9) – (11), (14) – (17) правого полупространства вводится значок вектора с правым направлением и верхний значок «+»:

, , , ,

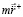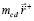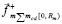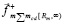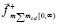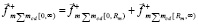, . (18)

Пусть продольная ось левой радиальной силовой линии лежит на [o, – ∞). Тогда вдоль нее действуют все силы соответственно по модулю равные (18), но они направлены противоположно силам (18). В обозначение противоположно направленных сил вводится значок вектора с левым направлением, верхний значок «-», меняется знак в их индексах:

, , , ,

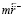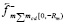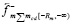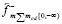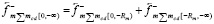, . (19)

В (18), (19) значки вектора соответствуют направлению вектора вдоль полупрямой, верхние значки «+» и «-» различают принадлежность правому и левому полупространству (полуплоскости, полупрямой). В состоянии покоя тела относительно точки o

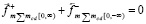, (20)

или 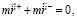и аналогично уравновешены действия составляющих сил:

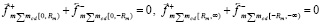. (21)

Равенства (20), (21) по построению верны для радиальных и полубесконечных цилиндров.

Инерция тела при нарушении покоя. В состоянии покоя тела относительно точки o суперпозиция магнитного поля ±среды правого полупространства действует на контуры линейных ±пар правого радиального цилиндра вдоль [0, Rm) исключительно из правого полубесконечного цилиндра, со стороны [Rm, ∞). Действие является постоянным – магнитный поток со стороны рассматриваемой суперпозиции не меняется. Внутри и вне радиального цилиндра силовые линии ортогональных ±пар определяют неоднородность магнитного поля. Площадь контура любой линейной ±пары правого радиального цилиндра за единицу времени пересекает одно и то же (в среднем) количество силовых линий ортогональных ±пар правого полубесконечного цилиндра. Его механическое действие на тело выражает сила 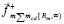из (18). С противоположной стороны на контуры линейных ±пар левого радиального цилиндра, вдоль [0, – Rm), действует магнитный поток из левого полубесконечного цилиндра, со стороны [– Rm, – ∞). Его механическое действие на тело выражает сила 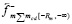из (19). Согласно (21), сумма их действий равна нулю. Пусть теперь к центру тяжести тела o по направлению правой полупрямой [o, ∞) приложена сила 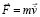, которая действует некоторый «сколь угодно» малый (в макроскопическом измерении), но фиксированный промежуток времени Δt. Конкретно в качестве Δt принимается время соударения двух абсолютно твердых тел при передаче механического импульса. Этот промежуток времени считается одинаковым для действия рассматриваемой силы и для передачи механического импульса, он будет называться квантом времени и обозначаться Δt = Δtquantum = const. Действие 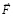рассматривается только в этот квант времени и является интерпретацией действия механического импульса. Согласно формуле силы, тело начнет движение с ускорением 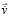в направлении 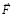. Скорость возрастает:

.

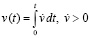Ускоренное движение продолжится в течение времени Δtquantum. Вместе с телом в том же направлении, с таким же ускорением, будут смещаться все радиальные силовые линии. Правый радиальный цилиндр будет смещаться вдоль промежутка [0, Rm). Двигаясь с ускорением навстречу магнитному потоку со стороны правого полубесконечного цилиндра, направленному вдоль [Rm, ∞), площадь контура каждой линейной ±пары правого радиального цилиндра будет пересекать в единицу времени возрастающее количество силовых линий ортогональных ±пар, входящих в правый полубесконечный цилиндр. Возникнет изменение магнитного потока через площадь контура каждой линейной ±пары правого радиального цилиндра. Поэтому во внешнем контуре каждой такой линейной ±пары возникнут вихри индукционного сопротивления. В силу их действия каждая линейная ±пара в правом радиальном цилиндре будет индукционно препятствовать вдоль [0, Rm) возникшему изменению магнитного потока. Внешний контур линейной ±пары меняет, по правилу Ленца, собственное магнитное поле навстречу меняющемуся магнитному потоку таким образом, чтобы препятствовать причине его изменения. Причина – ускоренное прямолинейное движение контура ±пары в направлении 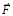. Возникнет противодействие именно ускоренному движению тела, то есть противодействие силе 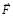. Этот процесс вместе с его аналогами во всех силовых линиях порождает инертность тела. В случае длительного действия силы столь же длительно меняется встречный магнитный поток и столько же времени длится индукционное сопротивление. Механизм сопротивления действию силы выражается в том, что индукционные токи на поверхности внешнего контура линейной ±пары имеют такое направление, что внешние полюса магнитных диполей этих вихревых токов оказываются одноименными полюсами S с внутренними полюсами S ортогональных ±пар правого полубесконечного цилиндра, суперпозиция вдоль [Rm, ∞) которых создает изменяющийся магнитный поток. Внешние полюса магнитных диполей вихревых токов отталкиваются от одноименных полюсов ортогональных ±пар. В результате каждая линейная ±пара правого радиального цилиндра индукционно препятствует вдоль [0, Rm) в течение времени Δt = Δtquantum изменению состояния покоя тела на состояние ускоренного движения по направлению .

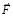Магнитный поток через площадь контура ±пары меняется не от того, что движутся элементы правого полубесконечного цилиндра, а от того, что этим элементам навстречу с ускорением движется сама линейная ±пара (вместе со всеми элементами правого радиального цилиндра). Элементы правого полубесконечного цилиндра остаются среднестатистически неподвижными относительно исходной точки покоя тела o, но они с ускорением 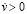меняют свое положение относительно пришедших в ускоренное движение элементов правого радиального цилиндра. C учетом прямолинейности рассматриваемых взаимодействий, ЭДС индукции ε выражается по закону Фарадея. В данном случае ЭДС противоположна знаку скорости увеличения магнитного потока:

.

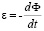Отсюда индукционное противодействие пропорционально ускорению движения тела и направлено против него. Во всех индукционных проявлениях эффекта Мейснера, наряду с вихревыми токами, продолжает в неизменном виде протекать постоянный ток – ток сверхпроводимости. Индукционные действия протекают взаимно независимо и синхронно со стационарными. Сохраняются все стационарные взаимодействия ±пар – гравитационные и электромагнитные, а также стационарное притяжение тела элементами ±среды. Следствием индукционного сопротивления является механическое действие на тело. В целом действие складывается из стационарного притяжения вдоль полупрямой [Rm, ∞), действующего по закономерности (15) с силой 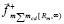, и с противодействующей силой индукционного отталкивания. Пусть индекс 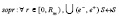указывает на суммарную силу сопротивления элементов радиального цилиндра вдоль [0, Rm), где S ↔ S соответствует отталкиванию одноименных магнитных полюсов, а сама сила сопротивления обозначается

.

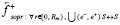Тогда сила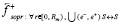

вычитается из силы стационарного притяжения. Полное значение силы (с сохранением обозначения и термина), действующей на тело вдоль правой полупрямой [0, ∞) со стороны всех контуров правого полупространства примет вид

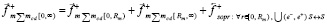(22)

или .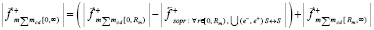

Стационарные взаимодействия вдоль левой полупрямой центрально симметрично отражают стационарные взаимодействия вдоль правой полупрямой, согласно (20), (21). Вследствие рассматриваемого действия на тело силы 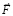магнитный поток через площади внешних контуров линейных ±пар левого радиального цилиндра будет изменяться вдоль [0, – Rm) в течение времени Δt = Δtquantum со скоростью, пропорциональной ускорению тела. Это произойдет в точности по тем же причинам, которые имеют место для правой полупрямой. В единицу времени через площадь внешнего контура линейной ±пары будет проходить возрастающее (в пропорции ускорению тела) количество силовых линий ортогональных ±пар левого полубесконечного цилиндра вдоль левой полупрямой [– Rm, – ∞). Принципиальная разница в том, что этот меняющийся магнитный поток имеет противоположное относительно правой полупрямой направление скорости изменения. Тело, а вместе с ним линейные ±пары левой радиальной силовой линии ускоренно удаляются от силовых линий ортогональных ±пар, соответственных левой полупрямой [– Rm, – ∞). Поэтому индукционное противодействие причине изменения магнитного потока будет заключаться в притяжении к ускоренно удаляющимся сдвоенным полюсам S ортогональных ±пар. Притяжение создадут контуры индукционных вихрей на внешних контурах линейных ±пар, ЭДС которых примет такое направление, что внешний полюс магнитных диполей индукционных вихрей будет N. Это создаст их притяжение к внутренним сдвоенным полюсам S ортогональных ±пар левого полубесконечного цилиндра, расположенным вдоль [– Rm, – ∞). Индукционное притяжение сложится (а не отнимется, как в правом полупространстве) со стационарным. Поэтому аналог (22) (с сохранением обозначения и термина) для левого радиального цилиндра примет вид

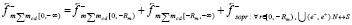(23)

и, соответственно,

.

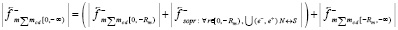В (23) индексы соответствуют левому полупространству, значки векторов – левому центробежному направлению стационарных сил и, соответственно, такому же индукционному сопротивлению вдоль левой полупрямой. Значки N ↔ S соответствуют притяжению разноименных магнитных полюсов N индукционных вихрей на контурах линейных ±пар вдоль промежутка [0, – Rm) и внутренних полюсов S ортогональных ±пар вдоль [– Rm, – ∞).

В итоге на тело во время действия силы 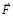, помимо этой силы, вдоль прямой (– ∞, ∞) действует сумма сил стационарного притяжения и индукционного сопротивления,

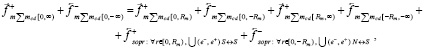
где стационарные силы удовлетворяют (20) и (21), а силы индукционного сопротивления равны по модулю, но обе направлены одинаково – противоположно 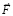. Отсюда

.

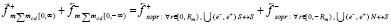При этом

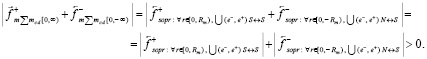
В правом полупространстве сила индукционного сопротивления

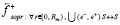
уменьшает действие стационарной силы пространственного притяжения .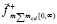

В левом полупространстве сила индукционного сопротивления

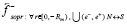
увеличивает действие стационарной силы пространственного притяжения .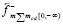

В результате сумма всех сил не равна нулю и направлена в сторону большей по модулю силы – противоположно 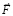, – что означает инертное сопротивление. Необходимо просуммировать стационарные и индукционные действия на тело по всем угловым направлениям правого и левого полупространств. При ускоренном смещении тела под действием силы 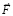радиальная силовая линия в правом полупространстве, составляющая угол φ с полупрямой [o, ∞) (с направлением 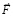), также движется навстречу магнитному потоку. Особенности по сравнению с движением вдоль полупрямой [o, ∞) состоят в следующем. Магнитный поток все равно образуется вдоль прямолинейного продолжения угловой радиальной силовой линии вследствие геометрической структуры ±среды. Этот магнитный поток присутствует каждый момент времени в каждом положении смещающейся угловой радиальной силовой линии, поэтому его можно считать стационарным. Меняется только линейное ускорение движения навстречу этому потоку. Для рассматриваемой угловой радиальной силовой линии ускорение встречного движения составит 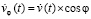. Соответственно, пропорционально этому косинусу изменятся все оценки сил индукционного сопротивления. Предполагается, что скользящий под углом характер взаимодействия с встречным магнитным потоком не ослабляет сил индукционного сопротивления, эти силы зависят исключительно от ускорения 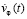тела в направлении встречного магнитного потока. Предполагается также, что оценки стационарного притяжения вдоль радиальной силовой линии, составляющей угол φ с направлением 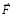, не изменятся. Аналогично, они не изменятся в левом полупространстве, изменение коснется только сил индукционного сопротивления. В результате

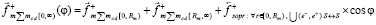
и, соответственно,

.

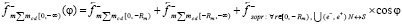В правой полуплоскости сумма проекций рассматриваемых сил на полупрямую [o, ∞) (без учета дискретизации) примет вид

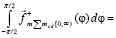
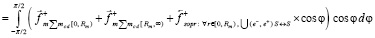
или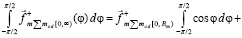

,

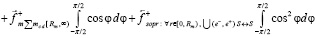что влечет

.

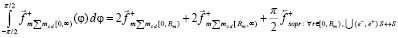Во всем правом полупространстве сумма проекций данных сил на полупрямую [o, ∞) выразится как

,

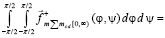
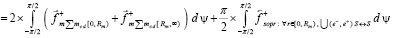отсюда

.

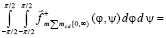
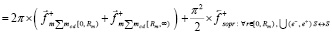Аналогично, в левом полупространстве сумма проекций сил стационарного притяжения и индукционного сопротивления на полупрямую [o, – ∞) выразится как

.

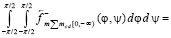
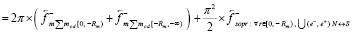Суммирование этих сил влечет

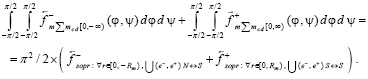(24)

Сила индукционного противодействия направлена противоположно 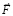, и по модулю равна

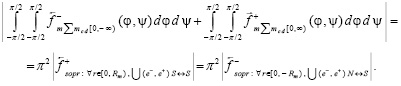(25)

Полная сила индукционного сопротивления (24) приложенной к телу силе 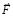ниже обозначается 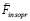, индекс insopr соответствует индукционному сопротивлению (инертности), знак вектора указывает направление, противоположное 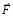. Силы индукционного сопротивления вдоль правой и левой полупрямой пропорциональны ускорению тела, создаваемому силой 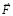, приложены к телу массой m, поэтому

,

,

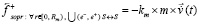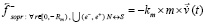где 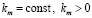, – коэффициент пропорции, значение которого неизвестно.

Сила 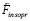приложена к тому же телу. С учетом (24)

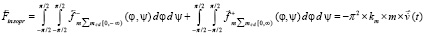
или

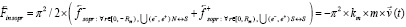. (26)

Согласно (26) .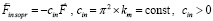

Движение тела по инерции после прекращения действия силы. Когда по истечении времени Δt = Δtquantum действие приложенной силы 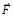прекратится, тело окажется под действием ранее возникшей силы индукционного сопротивления 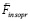, причем исключительно под действием одной этой силы (стационарные силы уравновешенны). Согласно формуле силы, тело вместе со своими силовыми линиями начнет ускоренное движение в обратную (противоположную 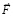) сторону с ускорением 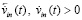и скоростью 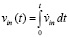. В левом (аналогично, в правом) полупространстве это ускоренное движение необходимо создаст изменение магнитного потока через площадь контуров линейных ±пар каждого радиального цилиндра. В единицу времени через площадь внешнего контура линейной ±пары будет проходить возрастающее (в пропорции ускорению) количество силовых линий ортогональных ±пар левого полубесконечного цилиндра, ось которого на [– Rm, – ∞). Аналогичное изменение магнитного потока будет происходить в правом полупространстве. Поэтому весь рассмотренный ранее процесс индукционного сопротивления повторится с обратным знаком, в левом и правом полупространстве (процесс вторичного индукционного сопротивления), но теперь именно по отношению к силе 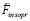. Соответственно, воспроизведутся все индукционные процессы и описывающие их соотношения, начиная с (14) и заканчивая (26), при условии изменения обозначений. В изменяемых обозначениях 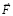заменяется на 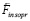, индексом in отмечаются все рассматривавшиеся ранее силы, ускорения и скорости. Аналогично (22), (23), с учетом обратного направления вторичного индукционного сопротивления,

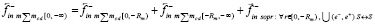(27)

и 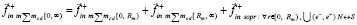. (28)

Стационарные силы от индукционного сопротивления не зависят, они остаются такими же, как в (22), (23), поэтому заново индексировать их индексом in в (27), (28) было не обязательно. В процессе вторичного индукционного сопротивления силе 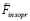создается дополнительная сила индукционного притяжения 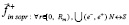к элементам правого полубесконечного цилиндра, вдоль [Rm, ∞), и создается дополнительная сила индукционного отталкивания 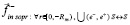от элементов левого полубесконечного цилиндра, вдоль [– Rm, – ∞). Обе дополнительные силы равны по модулю и одинаково направлены (противоположно 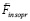). Аналогично предыдущему, полное действие на тело, обозначаемое 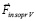, в условиях вторичного индукционного сопротивления примет вид

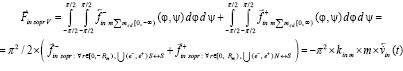(29)

и 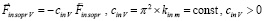. Сила 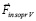вторичного индукционного сопротивления силе 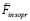из (25) направлена ей противоположно. Согласно (29), по модулю сила 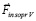равна удвоенной силе вторичного сопротивления в полупространстве. В результате действия силы 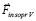восстанавливается направление движения тела, априори созданное силой 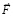. Тело будет двигаться под действием силы 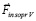по той же (с обратным направлением действия) причине, по которой сопротивлялось действию силы 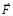: в центробежном направлении в правом полупространстве притяжение больше, чем в центробежном направлении в левом полупространстве. Поэтому тело движется в центробежном направлении в правом полупространстве, уже после прекращения действия 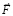. В силу природы индукционного сопротивления

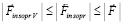. (30)

Cкорости перемещения тела по модулю не превышают скорости, созданной силой :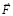

.

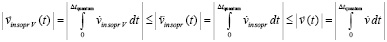Из (26) и (30) 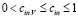и .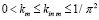

На данный момент открыт вопрос, будет ли во все дальнейшее продолжение времени скорость движения 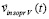постоянной и будет ли сила 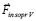иметь нулевое значение, то есть будет ли это движение движением по инерции? Для ответа принципиально, что после прекращения действия 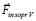порождавшие эту силу вихревые токи в радиальных силовых линиях не исчезнут (они постоянны во времени и не затухают в неизменяющемся магнитном поле). Коль скоро вихревые токи сохраняются постоянно, они постоянно взаимодействуют с внешним магнитным полем. Это внешнее поле как суперпозиция действия ортогональных ±пар принадлежит бесконечным продолжениям радиальных цилиндров, а взаимодействующие с этим полем магнитные диполи вихревых токов принадлежат контурам линейных ±пар радиальных цилиндров. Если природа движения по инерции и есть такое постоянное действие на тело со стороны ±среды, то почему это действие не создает ускорения?

Функция, описывающая вторичный индукционный процесс при передаче механического импульса. Ответ на вопрос могут дать особенности индукционного процесса. Передача импульса силой 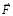происходит крайне быстро – за время Δtquantum соударения двух абсолютно твердых тел. Можно предположить, что действие суммы индукционных сил 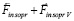переходит в аналитически гладкую функцию, которая монотонно приближается к нулю, нигде не равна нулю, при этом за соизмеримое с промежутком Δtquantum время принимает близкие к нулю значения. Асимптотическое стремление к нулю продолжается до бесконечности, не означая равенства нулю ни в один момент времени. Если интеграл от такой функции монотонно, с высокой скоростью стремится к постоянному значению, это влечет постоянство скорости движения тела. Как компонент конструируемой суперпозиции вводится функция

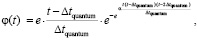
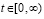, (31)

где α ≥ 102, которая будет применяться в следующих ограничениях. Действие индукционных сил рассматривается c момента окончания действия силы 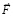, после первого кванта времени. В суперпозицию не включается действие силы 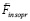в первый квант времени. Дальнейший отсчет времени действия суммы индукционных сил начинается с нуля уже после первого кванта времени. Искомая суперпозиция строится с момента вторичного индукционного сопротивления. Действие индукционных сил разделяется на два кванта времени переходного процесса, 0 ≤ t ≤ Δtquantum, и на неограниченное продолжение времени 2Δtquantum < t < ∞. Этому соответствует φ(0) = –1, φ(Δtquantum) = 0, φ(2Δtquantum) = 1. В начале переходного процесса φ(t) отрицательна, затем переходит через ноль, через два кванта времени – положительна. Она остается положительной за пределами 2Δtquantum. Эта функция выбрана в качестве весового множителя для модуля силы 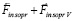. Пусть Δt1 quantum означает конец первого кванта времени, когда закончилось действие силы 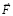. Обе силы индукционного сопротивления формально доопределяются с добавлением индекса def:

;

;

.

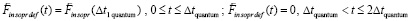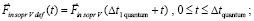
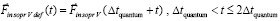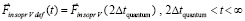Здесь 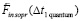– вектор индукционного сопротивления силе 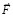на исходе предшествовавшего кванта времени, 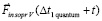– вектор индукционного сопротивления силе 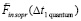в последующий квант времени, который принят за первый в новый промежуток времени, в правых частях – ранее описанные силы индукционного сопротивления, 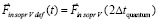– постоянный вектор вторичного индукционного сопротивления на бесконечном продолжении нового промежутка времени. Механическое действие на тело сил индукционного сопротивления обозначается FinV∞(t) и определяется как

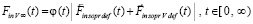, (32)

где 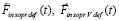определены непосредственно выше, подробно (32) примет вид

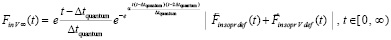. (33)

При t = 0, функция FinV∞(t) совпадает по модулю с силой 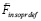и имеет одинаковый с ней знак.

При t = Δtquantum, функция FinV∞(t) равна нулю, что совпадает с .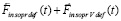

При t = 2Δtquantum, функция FinV∞(t) совпадает с модулем силы вторичного индукционного сопротивления 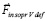и имеет одинаковый с ней знак.

При t > 2Δtquantum функция FinV∞(t) соответствует направлению 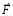, множитель

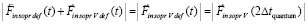
остается постоянным. Функция FinV∞(t) трактуется как модель действия индукционного процесса, которое переводит тело в состояние движения по инерции. Имеют место соотношения

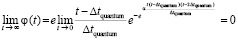, и .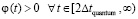

В силу (30) и согласно (31) суммы сил в правой части (33) конечны. Отсюда

, .

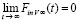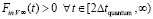Силы 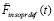, 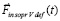противоположны по направлению, поэтому, с учетом (30),

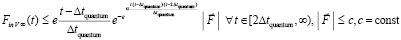. (34)

Очевидно, кроме того, что

.

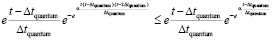
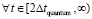Непосредственно ниже оцениваются отклонения FinV∞(t) от значений, которые функция имела почти сразу после выхода из отрезка времени длительностью 2Δtquantum. Пусть 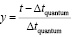. Для выполнения 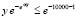достаточно, чтобы .

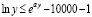Поскольку 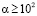, то последнее неравенство заведомо выполняется .

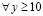Отсюда при 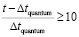, что равносильно 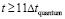, выполнено

,

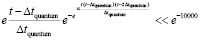в результате

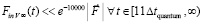. (35)

Стремление функции FinV∞(t) к нулю монотонно на промежутке 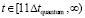, при этом согласно (33) она в любой момент времени больше нуля, а согласно (35) является исключительно малой величиной. Оценки можно усилить.

Чтобы выполнялось 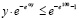, достаточно чтобы 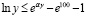. Тогда, поскольку 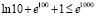, то 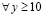заведомо выполнено

,

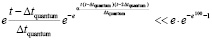отсюда

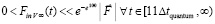. (36)

На промежутке t ∈ [11Δtquantum, ∞) сила FinV∞(t) не меняет направление, монотонно убывает к нулю со скоростью, такой, что за пределами 11 квантов времени верно (36). Необходимо убедиться, что после прекращения действия на тело силы 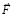не только ускорение очень быстро стремится к нулю, но и скорость достаточно быстро стремится к постоянному значению. Пусть рассматривается t0 = 1 + 2Δtquantum и v0 = v(t0). Из (33), (34) следует

.

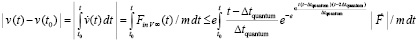Отсюда

и

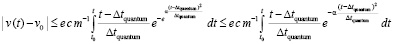
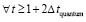
Следовательно, ,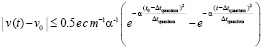

тогда ,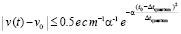

отсюда

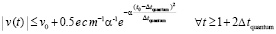. (37)

Неравенство (37) показывает ограниченность скорости на [1 + 2Δtquantum, ∞).

Кроме того, скорость монотонно возрастает, поскольку согласно (33)

,

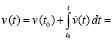
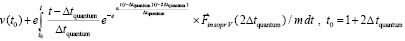следовательно, .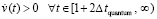

Ограниченная монотонно возрастающая функция имеет предел [21]:

.

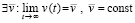В результате, после прекращения действия силы 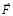, скорость тела не меняет знак и монотонно стремится к постоянному значению. Можно представить следующие оценки отклонения v(t) от v0 = v(t0). Из (37)

.

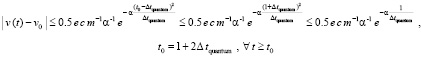Отсюда, при α = 100, Δtquantum = 0.0001, получится 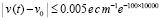или

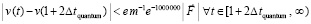. (38)

На бесконечном промежутке времени скорость тела будет отклоняться от данного начального значения на 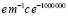. Предельный переход в неравенстве (38) влечет

.

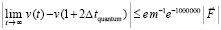Так что предельное значение скорости будет отклоняться на ту же величину – скорость «практически» постоянна сразу после передачи импульса. Еще одна иллюстрация малого отклонения скорости от начального значения получается по теореме Лагранжа о среднем значении. На любом отрезке [11Δtquantum, t] выполняется

.

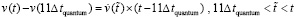Из того, что 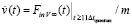, а также из (36) следует оценка

.

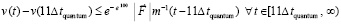При t = e100 получится

.

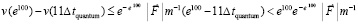Таким образом, по истечении времени t = e100 скорость будет отличаться от начального значения v(11Δtquantum) на величину 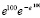, что достаточно мало на очень большом промежутке времени.

Согласно свойствам функции FinV∞(t), моделирующей действие индукционного процесса на тело, данное действие в неограниченное продолжение времени «практически» не порождает ускорения тела, а скорость «практически» постоянна.

Функция FinV∞(t) не обладает свойством единственности. Как основу для модели индукционного процесса можно рассматривать любую интегрируемую функцию, которая стремится к нулю, а ее первообразная в пределе является постоянной. Так, например, в качестве аналога φ(t) можно взять

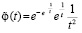или .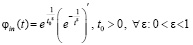

В любом случае функция FinV∞(t) не более чем модель реальности. Реальность же такова, что после передачи импульса тело движется под действием очень слабой, постоянной действующей силы. Эта сила является силой притяжения со стороны среды пространства сохранившихся индукционных вихрей в направлении движения, сложенной с аналогичной силой отталкивания в противоположном движению направлении. В реальности эта сила не создает ускорения потому, что уравновешивается встречной силой индукционного сопротивления: реальная сила встречает реальное индукционное сопротивление. Вихри индукционного сопротивления могут возникать, в частности, в любых ортогональных ±парах радиальных силовых линий под острыми углами к направлению движения. Сопротивление может быть и индукционным «трением» встречных элементов ±среды.

Инвариантность индукционных процессов передачи импульса относительно движения по инерции. Внешний магнитный поток меняется относительно элементов радиальной силовой линии тела в направлении, противоположном исключительно ускорению. Поэтому индукционные процессы, описанные для случая изменения положения покоя, произойдут при любом исходном положении тела, когда оно прямолинейно движется с постоянной скоростью, затем под действием импульса или силы меняет скорость. На данной основе изменения магнитного потока через площадь контура линейной ±пары радиального цилиндра, связанные с этим рассуждения и преобразования с учетом эффекта Мейснера, закона Фарадея и правила Ленца, инвариантны относительно движения тела по инерции в локальной системе отсчета. Возникает вопрос о различии индукционных состояний тела в предшествующем и новом движении по инерции. Плоскости индукционных вихрей контуров ±пар всегда ортогональны продольной оси радиального цилиндра, их ориентация зависит от направления импульса, как следствие, от направления движения по инерции. При этом вихри, возникшие в предшествующем состоянии инерции, сами по себе не исчезают. Тогда скольким направлениям предыдущих движений по инерции они должны соответствовать? Направление предшествующего движения по инерции отличается от направления текущего движения по инерции таким образом, что порождавшие их импульсы складывают векторы скоростей, и вектор текущей скорости является диагональю параллелограмма скоростей порождающих импульсов. Неясно, что в поведении индукционных вихрей до и во время передачи импульса, в кванты времени индукционного процесса, определило последующее направление вектора скорости. В контексте предложенного подхода возможны следующие варианты ответа. В момент передачи импульса инициация индукционных вихрей происходит вдоль каждой радиальной силовой линии, продольная ось которой составляет острый угол с направлением импульса. Это произойдет и вдоль направления предшествующего движения по инерции. Можно допустить, что вдоль предшествующего направления движения инициация индукционных вихрей заново произойдет с силой, соответствующей импульсу, породившему предшествующее движение. Новый импульс на момент своей передачи индукционно восстанавливает предшествующий импульс. Предшествующие индукционные вихри не исчезали, и, возможно, новый импульс «автоматически» восстанавливает их в активном состоянии. Если так, то это произойдет по всем радиальным силовым линиям тела. Наряду с тем передача нового импульса происходит без каких-либо изменений описанного ранее индукционного процесса. Пусть действие нового импульса описывается силой 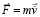в квант времени Δtquantum, а действие предшествующего импульса описывается силой 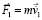, и, после повторной инициации, она действует в тот же квант времени без изменения закономерности. Тогда эти силы сложатся в силу 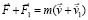, соответствующую суммарному импульсу. Вихревые токи сформируются под действием суммы сил 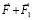точно так, как было описано их формирование под действием силы 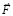в состоянии покоя. Под действием 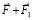сложатся ускорения 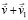, этой сумме будет соответствовать сумма скоростей 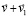. Пройдя через нулевое начальное значение в процессе вторичного индукционного сопротивления, эта сумма на выходе процесса передачи импульса преобразуется в сумму двух скоростей движения по инерции, что определит окончательное направление движения: 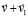. Ориентация магнитных диполей вихревых токов будет взаимно однозначно соответствовать движению по инерции именно в этом направлении. Можно отдельно рассмотреть предположение, что окончательное сложение скоростей происходит не с полным восстановлением индукционного процесса предшествовавшей передачи импульса, а с частичным – только на этапе завершения вторичного индукционного процесса. В этом случае на завершающем этапе складываются две силы: 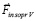и 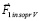. С весовыми функциями они переходят в силы, модули которых имеют значения FinV∞(t) и F1inV∞(t). Обе эти силы за кванты времени переходят к асимптотическим значениям скоросте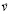й и 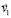, притом что их сложение могло произойти в процессе частичного индукционного восстановления предшествующего индукционного процесса. При таком частичном восстановлении каждая из двух скоростей проходит через начальное нулевое значение. Последующее сложение ускорений от обеих сил повлечет сложение скоростей. В рассматриваемом допущении ориентация магнитных диполей вихревых токов должна сформироваться на этапе сложения сил вторичного индукционного процесса как следствие взаимодействия индукционных вихрей на контурах линейных ±пар с ортогональными ±парами полубесконечного цилиндра, соответственного суммарному направлению. Это окончательно повлечет ориентацию диполей в соответствии направлению движения вдоль получившейся суммы скоростей 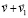. В обоих случаях в индукционном процессе передачи импульса задействованы два состояния тела – текущее и предшествующее состояния его движения по инерции (или локального покоя). При этом в текущем состоянии движения тела по инерции индукционные вихри ориентированы единственным образом – по направлению текущего движения. Пусть ортогонально направлению движения через центр тяжести тела o проведена центральная плоскость, разделяющая пространство на полупространство вдоль направления движения и на противоположное полупространство. Пусть рассматривается продольная ось радиального цилиндра, которая направлена вдоль движения. Тогда магнитные диполи вихрей на контурах линейных ±пар ориентированы полюсами N по направлению движения в соответствии индукционному притяжению к сдвоенным противоположным полюсам S ортогональных ±пар полубесконечного цилиндра. В противоположном полупространстве, на диаметрально противоположном радиальном цилиндре, магнитные диполи вихрей на контурах линейных ±пар ориентированы полюсами S противоположно направлению движения в соответствии индукционному отталкиванию от сдвоенных одноименных полюсов S ортогональных ±пар полубесконечного цилиндра. Те и другие магнитные диполи вдоль направления движения своими внешними полюсами образуют комбинацию

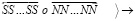, (39)

разделенную центром тяжести тела o в противоположных радиальных направлениях (направление движения указывает стрелка 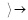). Такая же ориентация диполей имеет место вдоль каждой центральной прямой, расположенной под острым углом к направлению движения. В результате в полупространстве вдоль направления движения (тела по инерции) вся полусфера радиальных силовых линий ориентирована полюсами N по направлению движения, а вся противоположная ей полусфера радиальных силовых линий тела ориентирована полюсами S противоположно направлению движения. Индукционные вихри тела в покое на поверхности небесного тела примут ориентацию поверхности, поскольку переход в покой ему обеспечит именно импульс от «неподвижной» поверхности. Если предшествующее движение по инерции происходило в границах движения небесного тела, например, на поверхности Земли, то все импульсы со скоростями, меньшими скорости суточного вращения, дадут телу ориентацию индукционных вихрей в результате сложения скорости движения со скоростью суточного обращения земной поверхности. На входе и выходе процесса передачи импульса важны только скорость и направление движения тела по инерции – в текущем и предшествующем состоянии – при их сопоставлении в локальной системе отсчета, привязанной к центру гравитации.

Проявления индукционных сил инерции. Малые величины индукционных сил исключают наглядное проявление в телах с небольшой массой подобно тому, как тела с малой массой не проявляют видимого гравитационного взаимодействия между собой. Доступность их проявлений ограничивается еще и тем, что они происходят внутри радиальных цилиндров столь малого диаметра, что он сопоставим с диаметром конечного множества ±пар. Поля инерции существуют, они действуют, но в макроскопическом измерении, в небольших телах, наличие их элементов и их действие не обнаруживается. Однако при взаимодействиях массивных движущихся тел действия полей инерции могут проявляться наглядно. Движущиеся по инерции тела имеют ориентированные поля инерции в соответствии (39): такую комбинацию магнитных диполей вихревых токов линейных ±пар радиальных силовых линий тело имеет при движении в направлении от S к N («слева направо»). Если два тела движутся по инерции в одинаковом направлении (и еще не поравнялись), то они ориентированы друг на друга противоположными полюсами магнитных диполей, суперпозиции их полей создадут взаимное притяжение тел. В продолжение движения то же произойдет после обгона одного тела другим. Согласно (39) такое взаимодействие схематично представлено непосредственно ниже

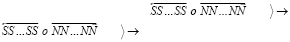(40)

или, после обгона одного тела другим,

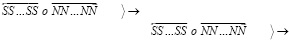(41)

где o – центр тяжести тела, стрелка 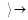указывает направление движения каждого тела.

Если два тела движутся по инерции во встречном направлении (и еще не поравнялись), то они ориентированы друг на друга одноименными полюсами магнитных диполей вихревых токов линейных ±пар радиальных силовых линий, суперпозиции их полей создадут взаимное отталкивание этих двух тел. То же произойдет в продолжение движения после «обгона» одного тела другим.

Такое взаимодействие схематично представлено в виде

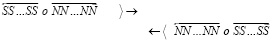(42)

или, в продолжение движения, после «обгона» одного тела другим

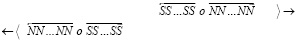(43)

В результате два тела, движущиеся по инерции навстречу друг другу, будут взаимно отталкиваться суперпозициями одноименных полюсов магнитных диполей вихревых токов ±пар радиальных силовых линий. То же произойдет после «обгона» одного тела другим. В момент, когда в положении (40) (или (42)) тела поравняются в движении, они должны взаимно отталкиваться (или, соответственно, притягиваться), но поскольку это сравнительно кратковременно (взаимная ориентация вследствие движения быстро восстановится), то в целом незначительно отразится на силе их взаимного притяжения (или, соответственно, отталкивания). Ниже взаимодействия двух тел на основе взаимной ориентации вихревых магнитных диполей (40) – (43) для краткости именуются индукционными. В процессе индукционных взаимодействий сохраняются все свойства стационарных полей. Сохраняется притяжение по закону всемирного тяготения. Индукционное взаимодействие тел всегда будет частью составных, где одно составляющее – гравитационное притяжение. Расположенные под острым углом относительно направлений движения радиальные силовые линии двух тел сохранят взаимную ориентацию диполей вихревых токов. Именно, при одинаковом направлении движения ориентация диполей с точностью до значения острого угла соответствует (40), (41), при встречном – (42), (43). Соответственная дипольная ориентация в случае большой массы проявляется как суперпозиция в локальной области пространства, а не как взаимодействие на большом расстоянии двух отдельных ±пар. Индукционные вихри в результате воздействия на тела сил, приводящих их в движение, с соответственной ориентацией магнитных диполей возникают также в контурах всех ±пар, входящих в структуру нуклонов в ядрах атомов каждого из двух тел. Сила индукционного взаимодействия двух движущихся тел принципиально отличается от силы индукционного взаимодействия тела с ±средой. Последняя, FinV∞(t), подчиняется закономерности (33), убывает со скоростью (34), (37) и, будучи не равна нулю, является очень слабой. Она определяется взаимодействием индукционных вихрей с ортогональными ±парами бесконечного продолжения радиального цилиндра. Взаимодействие двух тел, движущихся по инерции, определяется взаимодействием между собой индукционных вихрей исключительно линейных ±пар силовых линий и атомных ядер этих тел. Множество ориентированных вихрей локально сконцентрировано в структурном состоянии на сравнительно небольших расстояниях (в отличие от бесконечных пространственных состояний со стохастическим хаосом элементов). При этом взаимодействие индукционных вихрей с ортогональными ±парами радиальных силовых линий другого тела компенсируется их взаимодействием с линейными ±парами. Но именно на тех же контурах линейных ±пар располагаются взаимодействующие индукционные вихри, магнитные диполи которых определяют ориентацию поля инерции и доминирующее индукционное взаимодействие между двумя телами. Можно предположить, что эти вихри (при движении по инерции они в стационарном состоянии) взаимодействуют по закономерностям близкодействия – в соответствии с (8). В результате действие переходит на тело, отсюда следует аналог (9), (10). Предполагается изменение только коэффициентов:

,

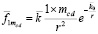или,

,

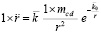где mcd – то же, что раньше, чертой отмечены новые коэффициенты, значения которых неизвестны. Действие тела массой M на тело массой m примет вид

.

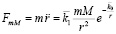Индукционное взаимодействие зависит от взаимных направлений движения двух тел, поэтому добавляется множитель в виде косинуса угла между направлениями движения:

,

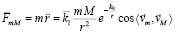где 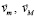– скорости движения тел с соответственной массой, 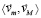– обозначение угла между направлениями, 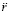– здесь и ниже соответственное ускорение. В данных соотношениях скорость движения отсчитывается относительно общего центра гравитации, в системе отсчета, фиксированной в этом центре. Конкретно, это система декартовых координат, с центром в центре гравитации, с координатной плоскостью, расположенной в плоскости эклиптики. Естественно предполагать, что сила индукционного взаимодействия пропорциональна величинам рассматриваемых скоростей, с изменением обозначения

.

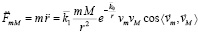В обозначении скалярного произведения 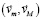формула примет вид

.

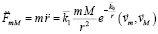Соотношение определяет действие тела массой M на тело массой m вдоль линии центров двух тел с учетом скоростей движений. Обратное действие тела массой m на тело массой M выражает соотношение

,

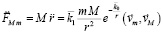где индексы силы 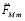меняются местами. Силу 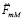можно записать в форме с механическими импульсами

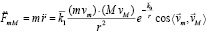
или

,

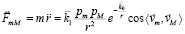где pm = mvm, pM = MvM.

При больших массах и высоких скоростях индукционные взаимодействия должны проявляться, поскольку они пропорциональны произведениям масс и скоростей, точнее, произведениям импульсов (в отличие от взаимодействия тела со средой). Можно ожидать, что эти силы проявляются при движениях небесных тел на близких друг от друга расстояниях вдоль соседних орбит. Орбитальные движения небесных тел прямолинейны и равномерны лишь в некотором приближении, тем не менее взаимная ориентация на притяжение или отталкивание должна сохраняться. В «наглядном» приближении суточное вращение поверхностей планет и звезд тоже можно рассматривать как движение по инерции. У небесных тел поведение индукционных вихрей на контурах линейных ±пар радиальных цилиндров связано, кроме того, с ускорением. Центростремительному ускорению индукционные вихри с необходимостью противодействуют по причине изменения магнитного потока со стороны бесконечного продолжения радиального цилиндра.

Об индукционной природе приливов и отливов. Особенности приливных волн разнятся в зависимости от географической широты и рельефа береговых линий. Предлагаемая трактовка относится к периодическим приливо-отливным явлениям и не касается географической широты и рельефа берега. Канонические сведения заимствуются из [22, с. 63]: «Уровень моря в Бресте поднимается и опускается два раза в каждом интервале времени между двумя последовательными возвращениями Луны к верхнему меридиану. Средний промежуток времени между этими возвращениями равен 1.035050 суткам, так что интервал времени между двумя последовательными приливами равен 0.517525 суток (такой же период отливов)…». Итак, прилив в этом месте повторяется примерно через 12 часов, происходит на стороне Земли, обращенной к Луне, и одновременно на противоположной от Луны стороне. Существующие объяснения не отклоняются от классического. Прилив на обращенной к Луне стороне Земли объясняется притяжением к Луне, прилив на обратной от Луны стороне Земли – центробежной силой, возникающей от вращения Земли и Луны вокруг общего центра этих двух небесных тел [22]. При этом Земля рассматривается как однородный аморфный шар. Но гравитационное взаимодействие таких шаров происходит, как если бы вся масса каждого из них была сосредоточена в их точечных центрах. Наружный сферический слой не оказывает на центр никакого действия [23, с. 329]. Тогда спорно действие на сферический слой, и классическое объяснение не вполне корректно. Притом солнечный прилив на обратной от Солнца стороне Земли проблемно объяснять центробежной силой, возникающей от вращения Земли и Солнца вокруг общего центра. Два небесных тела в солнечной системе, если они движутся по инерции в одинаковом или противоположном направлении, должны подчиняться индукционным взаимодействиям – притягиваться или отталкиваться в соответствии с ориентацией (40) – (43). В данном случае одно тело – Луна, другое – вся вращающаяся в суточном обращении масса Земли. То и другое движение воспринимаются на поверхности как движение по инерции, в некотором приближении они таковыми являются. Луна и поверхность Земли вращаются в одинаковом направлении. Поэтому, в соответствии с (40), (41), на обращенной к Луне стороне Земли прилив вызывается индукционным притяжением земной поверхности (и всей вращающейся массы Земли) к Луне. На противоположной от Луны стороне движение всей вращающейся массы Земли направлено противоположно движению Луны. Поэтому прилив вызывается индукционным отталкиванием этой стороны земной поверхности (и вращающейся массы Земли) от Луны – в соответствии с (42), (43). Луна и поверхность Земли вращаются в одинаковом угловом направлении, угловая скорость вращения Луны вокруг центра Земли в ≈27 раз меньше, чем угловая скорость суточного вращения Земли. В процессе вращения точка поверхности Земли будет «равняться, обгонять и догонять» точку кратчайшего расстояния до Луны за период обращения Луны вокруг Земли ≈27 раз. Поэтому поле инерции Луны и поле инерции части поверхности Земли, обращенной к Луне, будут «практически» ориентированы на постоянное притяжение. В то же время поле инерции Луны и поле инерции вращающейся части Земли, обращенной противоположно Луне, «практически» ориентированы на постоянное отталкивание. Это объясняет лунные приливы (отливы) с периодом 12 часов (рис. 4). Влияние полей инерции на приливо-отливные явления заведомо следует отнести к слабым взаимодействиям. На открытой поверхности океана высота приливных волн достигает лишь одного метра (при наличии скалистых препятствий будет возрастать, например в заливе Фанди – до 16-18 метров).

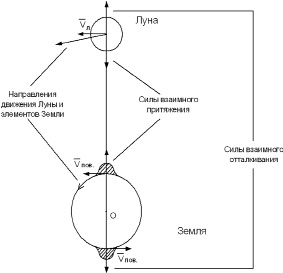
Рис. 4. Взаимное притяжение Луны с одинаково направленными и отталкивание с противоположно направленными элементами вращения земной поверхности

Иначе следует видеть причину солнечных приливов (отливов). В районе Бреста они имеют ту же периодичность, примерно 12 часов [22, с. 194]. Солнце и Земля вращаются вокруг своих осей в одинаковом направлении – против часовой стрелки, если смотреть со стороны северного полюса. Линейная скорость вращения Солнца на экваторе около 2 км/сек, что соответствует периоду около 25 земных суток (к полюсам период возрастает до 36 дней). Линейная скорость вращения Земли на экваторе 0.4651013 км/сек (к полюсам скорость падает). Поскольку в плоскости эклиптики обращение Солнца и Земли вокруг своих осей происходит в одинаковом направлении, то на сторонах поверхностей, обращенных друг к другу, линейные направления движения поверхностей взаимно противоположны. На противоположной от Солнца стороне Земли линейное направление движения поверхности совпадает по направлению с движением обращенной к Земле поверхности Солнца. Сопоставление с (42), (43) показывает, что поле инерции поверхности (и всей вращающейся массы) Солнца, обращенной к Земле, отталкивает поверхность Земли, обращенную к Солнцу, и притягивает противоположную часть поверхности Земли, обращенную от Солнца. В обоих случаях участки поверхности вдавливаются по направлению к центру Земли. Когда это происходит в океане, то вдавленная поверхность воды по краям центростремительного действия выталкивает наверх массу воды, что проявляется как приливный горб. При этом он больше на стороне, противоположной направлению вращения поверхности Земли (вследствие динамического противодействия направленному движению воды и ее накоплению в приливном горбе). На противоположной стороне Земли происходят аналогичные процессы, и приливный горб также больше на стороне, противоположной направлению суточного вращения. Вследствие сдвиговой механики взаимодействий солнечный прилив происходит через 12 часов с запаздыванием к положению точки максимального действия (рис. 5). Вместе с поверхностью вращается вся масса Солнца, которая участвует в создании поля инерции и в его индукционном взаимодействии со всей массой вращающейся вокруг своей оси Земли.

Наибольший подъем воды наблюдается, когда Солнце, Луна и Земля находятся на одной прямой линии. Это связано с резонансом лунных и солнечных приливных волн, при этом наибольший подъем воды происходит с запаздыванием до полутора суток [22, с. 196]. Запаздывание может быть следствием запаздывания приливной волны солнечного прилива с наложением на стандартное лунное запаздывание примерно на 50 минут. То и другое запаздывание сами по себе могут происходить от прохождения «мертвой зоны» в (40)–(43), когда тела выравниваются друг с другом и на время меняют характер индукционного взаимодействия.

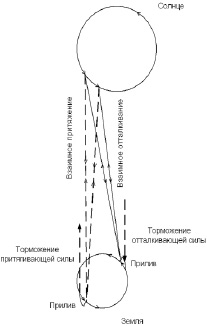
Рис. 5. Возникновение приливных горбов вследствие взаимодействия с вращающейся поверхностью Солнца

Если принять во внимание индукционное взаимодействие противоположных сторон тела вращения, то Земля приплюснута у полюсов, – у экватора диаметрально противоположные части поверхности сильнее отталкивают друг друга, поскольку вращаются в противоположных направлениях большей массой и с большей скоростью, чем у полюсов.

Об индукционных взаимодействиях планет. Поля инерции движущихся небесных тел создают взаимную ориентацию магнитных диполей вихревых токов вдоль касательной к орбите по направлению движения в разновидностях (40) – (43). В частности, это относится к близко расположенным планетам на соседних орбитах в Солнечной системе. Они движутся примерно в плоскости эклиптики, в одном направлении. Если между касательными в точках сближения образуется острый угол, то поля инерции ориентированы на взаимное притяжение. Если сближение происходит вблизи афелия (перигелия) орбиты, то угол между касательными начнет возрастать, особенно если у одной из планет вытянутая орбита. При некоторых параметрах движения может наступить момент, когда угол между касательными станет больше прямого и поля инерции двух планет станут ориентированными на взаимное отталкивание. Вслед за взаимным индукционным притяжением планеты начнут отдаляться друг от друга быстрее, чем это происходило бы в условиях только гравитационного притяжения. В подобном положении оказались Нептун и Плутон ко времени открытия Плутона в 1930 г. По расчетам Нептун прошел афелий 23 января 1963 г. От момента открытия Плутона Нептун приближался к точке своего афелия в течение 33 лет. В этот период Плутон двигался к перигелию своей орбиты, который он прошел 5 сентября 1989 г. Проходя перигелий, он оказался ближе к Солнцу, чем Нептун. У Плутона очень вытянутая эллиптическая орбита, она заходит внутрь орбиты Нептуна в проекции на плоскость эклиптики. Орбита Плутона сильно отличается от орбит планет Солнечной системы: у неё намного больший эксцентриситет (0.2488) и наклон к плоскости эклиптики 17.14º. Плутон находится с Нептуном в орбитальном резонансе 3:2. Когда Нептун прошел афелий (у него близкая к круговой орбита), а Плутон вдоль очень вытянутой орбиты продолжал двигаться к перигелию под углом наклона к эклиптике 17.14º, угол между касательными к орбитам в точках их расположения приближался к прямому или оказался больше него. Плутон делает оборот вокруг Солнца примерно 248 лет, Нептун – 165 лет, он монотонно увеличивает расстояние от точки сближения с Плутоном, продолжающим движение к перигелию. Поэтому угол между касательными к орбитам в точках положения растет, а на рост угла влияет сильная вытянутость орбиты Плутона и большой наклон к эклиптике, рост продолжается по ходу опережающего движения Нептуна. В результате Плутон, вначале притягивавшийся полями инерции Нептуна, помимо гравитационного притяжения, начнет испытывать ослабленное или отталкивающее действие полей инерции Нептуна. Масса Нептуна 1.02413×1026 кг, масса Плутона (1.303±0.003)×1022 кг. Нептун в ≈104 раз массивней, поэтому оказывает на Плутон сильное возмущающее действие. Вследствие орбитального резонанса аналогичный момент сближения («вложения» орбит) повторяется раз в 495 лет. Индукционное возмущение орбиты Плутона оказывается периодическим, чем создает отличие от орбит других планет вытянутостью и большим наклоном к эклиптике. Это не единственная причина, по которой Плутон мог периодически индукционно отталкиваться от Нептуна. Более существенно то, что Плутон представляет собой двойную планетную систему: его наибольший спутник Харон обладает массой, составляющей примерно 0.15 массы Плутона, поэтому Плутон и Харон вращаются вокруг общего центра. При этом Харон движется по ретроградной орбите, то есть противоположно планетам Солнечной системы. Оказываясь «внутри» орбиты Нептуна, Харон в явном виде по обращенной к Нептуну стороне орбиты движется ему навстречу, что соответствует взаимной ориентации полей инерции Харона и Нептуна по схеме (42), (43). В этом положении Харон отталкивается от Нептуна. Общий с Плутоном центр вращения Харона сдвигается в сторону от Солнца, что оказывает возмущающее влияние на орбиту Плутона. Все обстоит даже более принципиально. Поскольку масса Харона около 0.15 массы Плутона, и они вращаются вокруг общего центра, то, собственно, в этой системе двойной планеты Плутон и Харон вращаются в одинаковом направлении вокруг общего центра. Тогда и Плутон вращается по локально-ретроградной орбите следом за Хароном вокруг общего с ним центра. Поэтому сам Плутон периодически оказывается в положении встречного по отношению к Нептуну небесного тела. Плутон и Харон обращаются по круговым орбитам вокруг общего центра масс на расстоянии 19 130 км друг от друга с периодом 6.38 суток. Отсюда Плутон периодически, с интервалом около 3 суток, отталкивается своим полем инерции от поля инерции Нептуна. Его отталкивание складывается с отталкиванием Харона с таким же периодом. Имеется еще одна причина возмущения орбитального движения Плутона: Тритон (масса 2.14×1022 кг – 0.29 массы Луны), наибольший спутник Нептуна, также движется по ретроградной орбите вокруг Нептуна, и той стороной на орбите, которая обращена к двойной системе Плутон-Харон, движется навстречу их вращению друг за другом. Поэтому обращенными друг к другу сторонами на своих локальных орбитах Тритон и Харон взаимно отталкиваются полями инерции, что смещает Плутон в сторону от Солнца. Таким образом, существует множественная причина индукционного возмущения орбиты Плутона, которая воспроизводится каждые 495 лет. Как результат Плутон имеет нестандартно вытянутую орбиту с большим наклоном к эклиптике.

Влияние центростремительного ускорения на возмущение орбит планет. В любом прямолинейном направлении от центра тела существует среднестатистически постоянный магнитный поток. В силу своей стохастической природы он не меняется, не зависит от начального положения тела, его равномерного и прямолинейного или любого другого движения. В случае передачи импульса телу или в случае действия на тело внешней силы меняется только одно: ускорение движения навстречу неизменному потоку, что равносильно изменению магнитного потока через площадь контуров линейных ±пар радиальных силовых линий тела. При этом индукционный ток в замкнутом вихревом контуре имеет такое направление, что ослабляет причину своего возникновения. Магнитные диполи вихревых токов ориентированы так, чтобы противодействовать изменению магнитного потока, индуцирующего эти вихревые токи. На эллиптической орбите планета имеет центростремительное относительно фокуса орбиты (Солнца) ускорение, которое влечет изменение магнитного потока через контуры линейных ±пар радиальных силовых линий планеты и порождает центробежное отталкивающее сопротивление вдоль радиус-вектора. В радиальной силовой линии планеты, направленной вдоль радиус-вектора, в контурах линейных ±пар, возникают индукционные вихри, препятствующие причине изменения магнитного потока через площадь этих контуров, то есть центростремительному гравитационному притяжению. Препятствие притяжению к фокусу орбиты создает притяжение в обратном направлении – к ±среде вдоль бесконечного продолжения радиус-вектора – в центробежном от Солнца направлении. Это может быть вызвано только усилением суперпозиции внешних полюсов N магнитных диполей вихревых витков, что усилит притяжение к сдвоенным внутренним полюсам S ортогональных ±пар в бесконечном продолжении радиус-вектора. В обратном, центростремительном, направлении усилятся внешние полюса S магнитных диполей вихревых витков, создавая индукционное отталкивание от сдвоенных внутренних полюсов S ортогональных ±пар в обратном продолжении радиус-вектора. Следовательно, вовне радиус-вектора орбиты у полей инерции планеты появится ориентация вида (39) с полюсом N вовне в центробежном направлении (полюс S поддерживает отталкивание в обратном направлении). Вектор соответственного механического действия сложится с вектором действия поля инерции вдоль касательной к орбитальному направлению движения, согласно ориентации (39) которого впереди по направлению орбитального движения находится также полюс N диполей вихревых контуров. При движении к перигелию, в окрестности перигелия, угол между обоими векторами острый, в перигелии – прямой, после прохождения перигелия – угол тупой. При этом суммарный вектор механического действия сильно отклонится от касательной вовне орбиты, сохранив острый угол с направлением движения. Очевидно, внутренний полюс S, отталкиваясь от одноименных полюсов ориентации (39) (позади движения), только усилит отклонение вектора механического действия от касательной. Аналогичным будет поведение суммарного вектора полей инерции планеты в окрестности афелия. Необходимо учитывать значения линейных и центростремительных ускорений, массы тел, но в любом случае имеет место отклонение векторов действия поля инерции вовне от орбитального направления. Когда орбита Плутона в окрестности перигелия «вложена» в орбиту Нептуна, это дополнительно увеличивает углы между векторами механического действия полей инерции. С ростом угла между радиус-векторами некоторое время эта тенденция будет нарастать, по меньшей мере ослабляя противодействие отталкивающим возмущениям. Это дополняет причины периодических возмущений движения Плутона.

О влиянии на окрестную ±среду вращающейся платформы интерферографа Саньяка. Согласно [2], на достаточно малом расстоянии от планеты ±среда движется вместе с ней в орбитальном направлении с орбитальной скоростью, в непосредственной близости от поверхности планеты ±среда движется в направлении и со скоростью вращения планеты вокруг своей оси. Этим объясняется постоянство скорости света в любом направлении на земной поверхности в опытах Майкельсона. Напротив, ±среда практически не увлекается ускоренным (или вращательным [4]) движением малых тел на земной поверхности, чем объясняется разница скоростей света в опытах Саньяка. На элемент ±среды в непосредственной близости от вращающейся платформы интерферографа действует сила гравитационного притяжения к Земле, которая в 1010 раз превосходит силу притяжения к участку платформы, поэтому элемент среды следует за поверхностью Земли, а не за вращающейся поверхностью платформы. Проделанные выше рассуждения относительно центростремительного ускорения планет можно применить к центростремительному ускорению любой точки вращающейся платформы. На точку платформы действует сила вдоль касательной по направлению вращения. Индукционное сопротивление этой силе направлено противоположно. Очевидно, и сила, и сопротивление действуют постоянно. Индукционное сопротивление притягивает элементы окрестной ±среды вдоль касательной в направлении, противоположном вращению (вдоль полубесконечного цилиндра, ось которого находится на касательной в рассматриваемой точке). На точку, кроме того, действует центростремительная сила. Индукционное сопротивление центростремительному ускорению притягивает элементы окрестной ±среды со стороны полубесконечного цилиндра в центробежном направлении вдоль продолжения радиус-вектора. В результате сложения индукционных сил элементы ±среды отклоняются от точки касания под острым углом к касательной в направлении, противоположном вращению. Таким образом, элементы окрестной ±среды платформы отдаляются вовне от каждой точки ее вращения в направлении, противоположном вращению. Вместе с оценкой превосходящего действия гравитационного поля это показывает, что элементы ±среды не увлекаются и не могут увлекаться вращающейся платформой интерферографа, поэтому скорость света по направлению вращения платформы отличается от скорости света в противоположном направлении.

Вместе с тем данные рассуждения не означают, что на астрономическом удалении от небесных тел ±среда не будет увлекаться телом, движущимся по инерции. Напротив, она будет увлекаться вслед за движением его силовых линий.

Об индукционных возмущениях орбитальных движений других небесных тел. Наибольший спутник Нептуна Тритон движется по ретроградной орбите вокруг Нептуна. Той стороной на орбите, которая обращена к Урану, Тритон движется в одном с ним линейном направлении. Поэтому он притягивается Ураном в соответствии с (40), (41), и Уран притягивается к Тритону. Это указывает дополнительный источник возмущения движения Урана в центробежном от Солнца направлении. Привлекает внимание наличие крупных спутников Сатурна с ретроградной орбитой. Например, спутник Сатурна Феба (масса – 8.289×1018 кг) по внешней стороне орбиты движется в противоположном относительно Урана направлении. Согласно ориентации (40), (41) Феба отталкивает Уран в центробежном от Солнца направлении. В рассматриваемом аспекте более существенно поведение крупных спутников планет с не ретроградной орбитой. Вращаясь вокруг планеты в том же направлении, что и планеты Солнечной системы, по обращенной к Солнцу стороне своей орбиты, эти спутники движутся навстречу внутренним планетам, расположенным между ними и Солнцем. Такие спутники могут проявить отталкивающее действие своих полей инерции по отношению к внутренним планетам. К числу таковых относятся наиболее крупные спутники Юпитера: Ио (8.93×1022 кг), Европа (4.8×1022 кг), Ганимед (1.48×1023 кг) и Каллисто (1.08×1023 кг). Эти и другие спутники Юпитера с не ретроградной орбитой вполне могут оказывать возмущающее индукционное действие на орбитальное движение Марса. Дополнительное влияние может оказать Луна (7.3477×1023 кг): обращенная к орбите Марса сторона ее орбиты направлена одинаково с орбитальным движением планет Солнечной системы. Во время противостояния на этой стороне своей орбиты Луна своими полями инерции притягивает поля инерции Марса, что может суммироваться с отталкивающим действием галилеевых спутников Юпитера и притяжением полей инерции Земли (в дополнение к гравитационному притяжению). В свою очередь Марс по этой же причине может оказывать возмущающее индукционное притяжение Луны. Кроме того, в том же направлении (индукционное отталкивание с внутренней стороны) будут действовать на Луну поля инерции Венеры и Меркурия, что в сумме может смещать точки лунной орбиты. Сходные рассуждения можно отнести к небесным телам с возмущенными орбитами пояса Койпера. Так, у Седны орбита вытянута с эксцентриситетом 0.8590486 и наклоном к эклиптике 11.9º. Но если движение по орбите является ретроградным, как, например, у транснептунового объекта 2008 KV42 , то возмущение выражается гораздо сильнее. Наклонение орбиты составляет 103º. Такие возмущения неизбежны, они естественно объяснимы, если учитывать индукционные взаимодействия объектов и планет Солнечной системы. То же можно сказать о возмущении комет. Комета Галлея движется по ретроградной орбите. Средний период обращения кометы Галлея составляет 76 лет. Орбитальный период изменялся от 76 лет (в 1986 г.) до 79.3 года (в 451 и 1066 гг.). Орбита кометы высоко эксцентрическая (эксцентриситет 0.9671429), наклонена под углом 18º к эклиптике. Такая вытянутость орбиты и отклонение от эклиптики связаны с индукционным взаимодействием полей инерции по ходу ретроградного движения кометы. Поля инерции и гравитации взаимно независимы, во всех рассматриваемых взаимодействиях небесных тел гравитационное взаимодействие неизменно подчиняется закону всемирного тяготения. Непосредственный источник индукционного возмущения движения небесных тел может представлять вращающаяся вокруг своей оси масса Солнца. Так, Меркурий, взаимодействуя с вращающейся в одинаковом направлении с его орбитальным движением массой Солнца, имеет весьма выраженное возмущение движения. Он движется вокруг Солнца по сильно вытянутой эллиптической орбите (эксцентриситет 0.205) на среднем расстоянии 57.91 млн км. Наклон орбиты к плоскости эклиптики равен 7º. Это коррелируется с наклоном к эклиптике оси вращения Солнца, который составляет с направлением на полюс эклиптики угол 7º15'. Продолжительность меркурианского дня равна продолжительности меркурианского года. Меркурий обращается вокруг Солнца в спин-орбитальном резонансе 3:2, то есть за два меркурианских года планета совершает три оборота вокруг своей оси. Есть еще одно обстоятельство, которое не стоит упускать из виду. В направлении, противоположном направлению орбитального движения Меркурия, вращается вокруг своей оси ближайшая к нему планета Венера. Это означает, что вращающаяся масса Венеры своей стороной, обращенной к орбите Меркурия, линейно направлена в ту же сторону, в какую движется Меркурий. Поле инерции вращающейся массы Венеры притягивает к себе Меркурий, что складывается с гравитационным притяжением к ней и в сумме может составить заметную силу притяжения Меркурия в центробежном от Солнца направлении. Оно вычитается из действия гравитации Солнца и индукционного притяжения его вращающейся массы. Масса Меркурия 3.3×1023 кг, Венеры – 4.87×1024 кг, Солнца – 1.98892×1030 кг. Периодическое сближение этих тел между собой происходит только в определённых точках орбит. Период обращения Меркурия вокруг Солнца 0.241 земного года, Венеры – 0.615 земного года. Поэтому Меркурий не реже чем два раза в год оказывается на наименьшем расстоянии от Венеры, что периодически усугубляет индукционные возмущения. Прецессия перигелия Меркурия составляет 574.10±0.65" (угловых секунд) за столетие в гелиоцентрической системе координат.

Выделяется также тот факт, что спутники Юпитера, движущиеся противоположно его вращению вокруг своей оси, медленно удаляются от его центра. Это можно объяснить их индукционным отталкиванием от массы Юпитера, вращающейся в направлении, противоположном их орбитальному движению.

Вращающаяся вокруг своей оси масса Солнца индукционно отталкивает движущуюся во встречном направлении Луну в ближайшей к Солнцу точке лунной орбиты. В диаметрально противоположной точке вращающаяся масса Солнца индукционно притягивает движущуюся в одинаковом с ней направлении Луну. Создается момент поворота плоскости лунной орбиты. Это согласуется с тем, что плоскость лунной орбиты отличительно наклонена к плоскости эклиптики под углом 5.14º, а к плоскости земного экватора – под углом 28.6º. Вращающаяся масса Солнца аналогично взаимодействует с вращающейся в суточном обращении массой Земли, что согласуется с наклоном земного экватора к плоскости эклиптики под углом 23º26'.

О создании движения без передачи импульса. В состоянии локального покоя тело симметрично по всем направлениям притягивается вдоль радиальных силовых линий к элементам ±среды. Если в одном из направлений притяжение станет меньше, то сумма притяжений в остальных направлениях создаст противоположное направление притяжения. Уменьшить притяжение в заданном направлении возможно, если в этом направлении ослабить структуру радиальных силовых линий. Это достижимо посредством сильного переменного электромагнитного поля с выбранной стороны тела, если экранировать воздействие этого поля по остальным направлениям. В качестве экрана можно взять металлический параболоид, жестко скрепленный с телом, а источник переменного поля заключить внутрь параболоида. Чем сильнее магнитное поле, тем больше нарушается сверхпроводимость контуров ±пар и соответственно ослабляется структура радиальных силовых линий. Чем выше частота колебаний возмущающего поля, тем эффективнее воздействие на структуру силовых линий. В одном из экспериментов [24] наблюдалось быстрое перемещение с постоянной скоростью сложенного вдвое полутораметрового изолированного алюминиевого провода диаметром 2 мм, свободно подвешенного на эластичной тесьме, когда на провод подавался переменный ток через амальгамированный разделенный медный контакт, свободно плававший в двух сдвинутых чашах ртути. На момент проведения эксперимента эффект был воспринят как побочный эффект искомого изменения веса [24]. Между тем электромагнитное поле нарушало структуру силовых линий инерции внутри сложенного вдвое проводника сильнее, чем снаружи, что создавало движение. В данном направлении активные исследования с применением электромагнитных полей проводятся в США, Великобритании и Китае.

Заключение

В работе вводится предположение о сверхпроводимости элементов вакуума и их индукционных свойствах, на основе которых объясняется инерция физических тел. Описаны механизмы взаимодействий элементов полей инерции и вакуумного пространства. Предложена модель индукционной природы инерции. Тело движется по инерции вследствие индукционного действия на него элементов среды вакуума, направленного вдоль движения. Это действие не создает ускорения, потому что уравновешивается индукционным «трением» встречных элементов вакуумной среды. Приведены примеры возмущений орбитальных движений, причины которых трактуются как взаимодействия полей инерции движущихся небесных тел.