Введение
Лекарства – это адаптивные молекулы. Они реализуют эту особенность, генерируя различные ансамбли прототропных форм и конформеров, которые зависят от окружающей среды. Среди впечатляющего количества доступных технологий вычислительного поиска и открытия лекарств количественные подходы к взаимосвязи структура – активность (QSAR), которые опираются на вычислительные дескрипторы квантовой химии, являются наиболее подходящими для моделирования адаптивных лекарств [1]. Действительно, вычислительные дескрипторы квантовой химии способны учитывать вариации внутримолекулярных взаимодействий учебных соединений, которые отражают их адаптивные склонности к межмолекулярному взаимодействию. Это позволяет разрабатывать причинные, интерпретирующие и разумно предсказывающие количественные модели взаимосвязи структура – активность и, следовательно, надежную химическую информацию, доработанную для разработки и открытия лекарств. В разработке причинно-интерпретирующих зависимостей используются приемы статистического метода анализа: линейные и регрессионные [2]. По множественным оценкам к перспективным методам исследования параметров структуры относятся квантово-химические вычисления [3]. Поиск количественной зависимости биологической активности от строения веществ является перспективным. Одной из проблем построения моделей прогнозирования биологической активности является наличие результатов исследования биологической активности. Способов замены экспериментальных данных существует огромное количество, для их построения применяются различные способы обучения и построения.
Производные антраниловой кислоты относятся к перспективным производным, с различными видами фармакологического действия [4–6].
Цель исследования – изучение причинно-следственной взаимосвязи «структура – противовоспалительная активность», созданной на основе квантово-химических вычислений в ряду амидов и гидразидов N– 2-фураноил замещенных антраниловых кислот поиска зависимости, описывающей биологическую активность.
Материалы и методы исследования
Для построения причинно-следственной модели при описании структуры использовали квантово-химические вычисления (программа Gaussian 03), прогнозирование противовоспалительной активности (AK_QSAR (противовоспалительная активность) [7]) и построение модели (Statistica 6).
Результаты исследования и их обсуждение
Молекулярное моделирование исследуемых соединений – двадцати пяти гомологов (1–25) амидов и гидразидов N– 2-фураноил замещенных антраниловых кислот проводили программой AK_QSAR (ПВА). Общая структура анализируемого объекта исследования приведена на рис. 1.
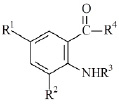
Рис. 1. Общая структура исследуемых соединений ряда с заместителями: R1, R2, R3, R4
Для проведения дизайна исследуемых соединений с помощью AK_QSAR (ПВА) осуществляли построение 25 структур (1–25) (рис. 2), общей химической структуры (рис. 1).
Результаты прогнозирования ПВА 25 соединений программой AK_QSAR (ПВА), определенной на модели «каррагенинового отека» [7] и структурные (квантово-химические) параметры описания структуры, представлены в табл. 1.
С использованием табл. 1 проведена обработка полученных данных статистического анализа в оценке объема выборки по каждому описательному параметру структуры. В качестве структурных параметров использовали результаты квантово-химических расчетов: напряженность (Е), потенциал (Пот) и заряд в модуле (|q|). Результаты проведенного статистического анализа, его обработки по критериям: коэффициент корреляции (R) и критерий Фишера (F) приведены в табл. 2 и 3.
Осуществлена обработка данных регрессионного исследования по значениям R (R > 0,500) и критерия Фишера (F > 6), результаты обработки приведены в табл. 4.
С использованием результатов отбора, приведенных в табл. 4, выбраны три набора дескрипторов в виде моделей (№ 1–3), основанные на объеме выборки со значениями R (R > 0,500) и F (F > 6): 1 модель (N = 15 соединений): ∑C (E), ∑H (пот), ∑C (|q|), ∑O (|q|), ∑H (|q|); 2 модель (N = 20 соединений): ∑C (E), ∑O (|q|); 3 модель (N = 25 соединений): ∑C (E), ∑C (пот), ∑C (|q|), ∑O (|q|), ∑H (|q|).
Регрессионное моделирование проводили методом пошагового исключения параметров по одному, количество структурных характеристик, равное двум, использовали в качестве минимального.
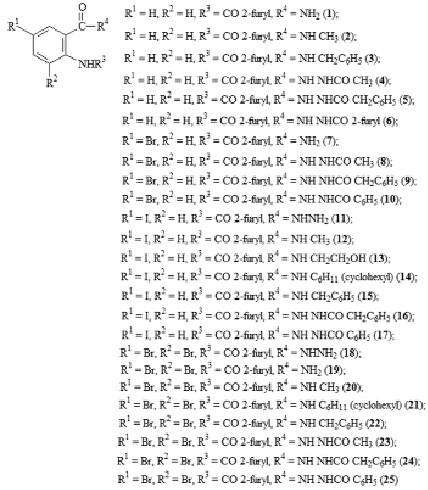
Рис. 2. Структуры исследуемых соединений (1–25)
Таблица 1
Прогнозируемые значения ПВА (ПВАрассч.) и структурные параметры соединений 1–25
|
№ |
ПВАрассч., % |
∑С (E) |
∑O (E) |
∑H (E) |
∑С (Пот) |
∑O (Пот) |
∑H (Пот) |
∑С (|q|) |
∑O (|q|) |
∑H (|q|) |
|
1 |
44,22 |
7,386 |
2,426 |
10,470 |
159,508 |
39,716 |
71,794 |
1,677 |
0,921 |
1,236 |
|
2 |
24,70 |
7,517 |
2,582 |
13,037 |
168,687 |
44,254 |
91,080 |
1,800 |
0,937 |
1,317 |
|
3 |
74,01 |
11,146 |
2,615 |
15,615 |
251,801 |
45,104 |
172,600 |
2,189 |
0,927 |
1,684 |
|
4 |
7,23 |
7,871 |
3,196 |
13,275 |
181,130 |
56,808 |
102,272 |
1,775 |
1,108 |
1,306 |
|
5 |
56,54 |
11,500 |
3,229 |
15,854 |
264,244 |
57,658 |
183,792 |
2,164 |
1,099 |
1,673 |
|
6 |
12,19 |
7,596 |
3,580 |
13,185 |
171,976 |
65,105 |
90,459 |
1,810 |
1,130 |
1,319 |
|
7 |
48,06 |
7,687 |
2,423 |
10,007 |
162,586 |
39,622 |
66,118 |
1,672 |
0,883 |
1,170 |
|
8 |
7,76 |
8,265 |
3,192 |
12,078 |
184,380 |
56,734 |
85,420 |
1,749 |
1,090 |
1,195 |
|
9 |
28,2 |
11,801 |
3,226 |
15,391 |
267,322 |
57,563 |
178,116 |
2,159 |
1,061 |
1,607 |
|
10 |
8,45 |
8,929 |
3,209 |
14,561 |
201,141 |
57,101 |
107,732 |
1,879 |
1,067 |
1,348 |
|
11 |
19,29 |
8,123 |
2,729 |
10,541 |
178,077 |
46,987 |
77,214 |
1,722 |
1,092 |
1,192 |
|
12 |
28,78 |
7,831 |
2,579 |
12,596 |
172,066 |
44,170 |
85,809 |
1,795 |
0,898 |
1,247 |
|
13 |
25,03 |
8,478 |
3,190 |
13,431 |
187,141 |
57,234 |
98,883 |
1,816 |
0,895 |
1,256 |
|
14 |
32,67 |
9,584 |
2,601 |
14,405 |
216,681 |
44,728 |
107,879 |
1,970 |
0,936 |
1,414 |
|
15 |
78,09 |
11,460 |
2,612 |
15,175 |
255,180 |
45,020 |
167,329 |
2,183 |
0,889 |
1,614 |
|
16 |
60,62 |
11,815 |
3,226 |
15,413 |
267,623 |
57,573 |
178,522 |
2,158 |
1,061 |
1,603 |
|
17 |
8,68 |
8,943 |
3,210 |
14,584 |
201,442 |
57,111 |
108,137 |
1,878 |
1,068 |
1,345 |
|
18 |
25,36 |
7,841 |
2,716 |
9,729 |
170,368 |
46,669 |
71,677 |
1,639 |
1,094 |
1,064 |
|
19 |
54,38 |
7,418 |
2,410 |
9,217 |
155,177 |
39,314 |
60,986 |
1,588 |
0,886 |
1,039 |
|
20 |
34,86 |
7,548 |
2,565 |
11,784 |
164,356 |
43,852 |
80,271 |
1,712 |
0,901 |
1,120 |
|
21 |
38,75 |
9,301 |
2,588 |
13,593 |
208,971 |
44,410 |
102,342 |
1,887 |
0,939 |
1,287 |
|
22 |
84,17 |
11,177 |
2,599 |
14,362 |
247,470 |
44,702 |
161,791 |
2,101 |
0,892 |
1,487 |
|
23 |
17,39 |
7,902 |
3,180 |
12,022 |
176,799 |
56,406 |
91,464 |
1,687 |
1,072 |
1,109 |
|
24 |
66,70 |
11,532 |
3,213 |
14,601 |
259,913 |
57,256 |
172,984 |
2,075 |
1,063 |
1,476 |
|
25 |
14,76 |
8,660 |
3,196 |
13,771 |
193,732 |
56,794 |
102,600 |
1,795 |
1,070 |
1,217 |
Таблица 2
Результаты статистического исследования зависимости «противовоспалительной активности (ПВА)» от суммарных структурных параметров по R и объему анализируемой выборки
|
Число БАВ |
Коэффициент корреляции (R) |
||||||||
|
∑С (E) |
∑O (E) |
∑H (E) |
∑С (Пот) |
∑O (Пот) |
∑H (Пот) |
∑С (|q|) |
∑O (|q|) |
∑H (|q|) |
|
|
10 |
0,488 |
0,581 |
0,159 |
0,439 |
0,569 |
0,459 |
0,481 |
0,608 |
0,550 |
|
15 |
0,604 |
0,529 |
0,314 |
0,557 |
0,517 |
0,571 |
0,610 |
0,565 |
0,637 |
|
20 |
0,538 |
0,466 |
0,181 |
0,482 |
0,459 |
0,496 |
0,486 |
0,524 |
0,474 |
|
25 |
0,632 |
0,437 |
0,250 |
0,579 |
0,426 |
0,588 |
0,579 |
0,520 |
0,535 |
Таблица 3
Результаты статистического исследования зависимости «противовоспалительной активности (ПВА)» от суммарных структурных параметров по F и объему анализируемой выборки
|
Число БАВ |
Критерий Фишера (F) |
||||||||
|
∑С (E) |
∑O (E) |
∑H (E) |
∑С (Пот) |
∑O (Пот) |
∑H (Пот) |
∑С (|q|) |
∑O (|q|) |
∑H (|q|) |
|
|
10 |
2,512 |
4,088 |
0,209 |
1,917 |
3,851 |
2,141 |
2,421 |
4,708 |
3,480 |
|
15 |
7,503 |
5,076 |
1,431 |
5,877 |
4,763 |
6,333 |
7,750 |
6,137 |
8,958 |
|
20 |
7,371 |
5,021 |
0,612 |
5,487 |
4,825 |
5,911 |
5,613 |
6,833 |
5,232 |
|
25 |
15,352 |
5,450 |
1,548 |
11,657 |
5,145 |
12,182 |
11,655 |
8,562 |
9,269 |
Таблица 4
Результаты отбора итогов корреляционного анализа объем выборки, R, F
|
№ |
Дескриптор |
Объем выборки |
R |
F |
|
1 |
∑C (E) |
15 |
0,604 |
7,503 |
|
2 |
∑C (E) |
20 |
0,538 |
7,371 |
|
3 |
∑C (E) |
25 |
0,632 |
15,352 |
|
4 |
∑О (E) |
15 |
0,529 |
5,076 |
|
5 |
∑C (пот) |
15 |
0,557 |
5,877 |
|
6 |
∑C (пот) |
25 |
0,579 |
11,657 |
|
7 |
∑Н (пот) |
15 |
0,571 |
6,333 |
|
8 |
∑C (|q|) |
15 |
0,610 |
7,750 |
|
9 |
∑C (|q|) |
25 |
0,579 |
11,655 |
|
10 |
∑O (|q|) |
15 |
0,565 |
6,137 |
|
11 |
∑O (|q|) |
20 |
0,524 |
6,833 |
|
12 |
∑O (|q|) |
25 |
0,520 |
8,652 |
|
13 |
∑H (|q|) |
15 |
0,637 |
8,958 |
|
14 |
∑H (|q|) |
25 |
0,520 |
8,562 |
Таблица 5
Результаты проверки уравнений регрессии связи ПВА со структурой на выборке из 6 соединений (26–31)
|
№ |
Уравнение регрессии |
Оценка прогноза ПВА |
|
|
Rпрогн. |
Sпрогн. |
||
|
1 |
ПВАрассч. 1 = 155,194 + 17,052 × ∑С (E) – 0,395 × ∑H (пот) – – 258,016 × ∑C (|q|) – 143,603 × ∑O (|q|) + 291,135 × ∑H (|q|) (R = 0,917; F = 9,51; S = 11,37; N = 15) |
0,714 |
13,45 |
|
2 |
ПВАрассч. 2 = 143,061 + 8,070 × ∑С (E) – 180,296 × ∑O (|q|) (R = 0,858; F = 9,85; S = 13,66; N = 10) |
0,426 |
24,71 |
|
3 |
ПВАрассч. 3 = 66,059 + 69,621 × ∑С (E) – 2,431× ∑C (пот) – – 105,922 × ∑C (|q|) – 94,481 × ∑O (|q|) + 92,233 × ∑H (|q|) (R = 0,897; F = 15,81; S = 11,65; N = 25) |
0,600 |
16,30 |
|
4 |
ПВАрассч. 4 = – 42,788 + 71,456 × ∑С (E) – 2,781× ∑C (пот) + + 36,339× ∑C (|q|) – 75,236 × ∑O (|q|) (R = 0,887; F = 18,46; S = 11,91; N = 25) |
0,592 |
16,03 |
|
5 |
ПВАрассч. 5 = – 209,418 + 106,599 × ∑С (E) – – 4,655 × ∑C (пот) + 117,299 × ∑C (|q|) (R = 0,872; F = 22,31; S = 12,30; N = 25) |
0,498 |
20,78 |
|
6 |
ПВАрассч. 6 = – 97,189 + 97,055× ∑С (E) – 3,696 × ∑C (пот) (R = 0,840; F = 26,55; S = 13,31; N = 25) |
0,537 |
17,41 |
По результатам регрессионного анализа проведен отбор значимых моделей с R: 0,700 и более, и значением F: 9 и более. Результаты обработки регрессионного анализа приведены в табл. 5.
Тестирование найденных моделей связи ПВА со структурой проводили на выборке из 6 соединений (26–31) (рис. 3), содержащей результаты экспериментального исследования ПВА [7], общей химической структуры (рис. 1).
Дескрипторы, используемые при расчетах ПВА соединений 26–31, приведены в табл. 6.
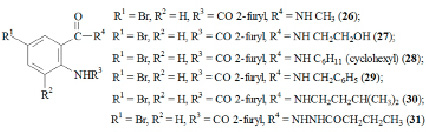
Рис. 3. Структуры исследуемых соединений, проверочная выборка 6 соединений (26–31)
Таблица 6
Структурные параметры 6 соединений (26–31)
|
№ |
ΣC(E) |
ΣО(E) |
ΣC(пот) |
ΣО(пот) |
ΣН(пот) |
ΣC(|q|) |
ΣО(|q|) |
ΣH(|q|) |
|
26 |
7,82 |
2,58 |
171,77 |
44,16 |
85,40 |
1,80 |
0,90 |
1,25 |
|
27 |
8,46 |
3,19 |
186,84 |
57,22 |
98,48 |
1,82 |
0,90 |
1,26 |
|
28 |
9,57 |
2,60 |
216,38 |
44,72 |
107,47 |
1,97 |
0,94 |
1,42 |
|
29 |
11,45 |
2,61 |
254,88 |
45,01 |
166,92 |
2,18 |
0,89 |
1,62 |
|
30 |
10,56 |
2,61 |
247,94 |
44,92 |
170,49 |
2,12 |
0,86 |
1,58 |
|
31 |
11,74 |
3,21 |
270,21 |
57,08 |
159,50 |
1,97 |
1,04 |
1,41 |
Таблица 7
Результаты прогноза противовоспалительной активности (ПВА рассч.) по уравнениям 1–6 и экспериментальные (ПВАэксп.) соединений (26–31)
|
№ п.п |
Ур-е 1 (ПВА рассч. 1) |
Ур-е 2 (ПВА рассч. 2) |
Ур-е 3 (ПВА рассч. 3) |
Ур-е 4 (ПВА рассч. 4) |
Ур-е 5 (ПВА рассч. 5) |
Ур-е 6 (ПВА рассч. 6) |
ПВА эксп., % |
|
26 |
26,47 |
44,17 |
32,82 |
35,66 |
34,81 |
26,61 |
19,55 |
|
27 |
29,77 |
49,97 |
40,05 |
40,99 |
36,11 |
33,71 |
21,15 |
|
28 |
45,86 |
51,50 |
39,76 |
40,33 |
34,45 |
31,88 |
63,65 |
|
29 |
64,13 |
75,10 |
76,96 |
78,60 |
80,28 |
71,65 |
60,25 |
|
30 |
55,19 |
72,42 |
37,30 |
34,21 |
10,87 |
11,34 |
31,65 |
|
31 |
44,41 |
49,67 |
48,99 |
37,31 |
14,48 |
43,34 |
35,65 |
Полученные результаты прогноза ПВА в сравнении с экспериментальными значениями (ПВАэксп.), определенные на модели «каррагенинового отека», представлены в табл. 7.
Заключение
В результате молекулярного дизайна 25 производных антраниловой кислоты получено 6 значимых моделей.
Уравнение 1 (пятипараметровое) по результатам проверки на независимой выборке имеет минимальное значение среднеквадратичной ошибки (Sпрогн. = 13,45), прогноза ПВА, среди полученных моделей, и максимальное Rпрогн. (Rпрогн. = 0,714) (коэффициент корреляции теоретических значений биологической активности с экспериментальными), в сравнительной оценке по отношению к найденным моделям.

