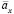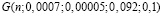Введение
Современный этап развития общественных социально-экономических отношений требует нетривиальных подходов к идеологии расчета пенсионных рент [1, с. 13–46, 170–194], что связано:
– с влиянием на страховой рынок таких непредсказуемых явлений, как эпидемии, природные катастрофы, социальные катаклизмы и т.п. [2–4],
– с появлением новых видов страховых и пенсионных услуг [5, 6].
Согласно работе Г.И. Фалина пожизненная рента определяется как денежная сумма, выплачиваемая человеку раз в год в течение его жизни [1, c. 170–172]. Для удобства расчетов такую денежную сумму принимают равной условной единице. Таким образом, пожизненную ренту можно определить следующей формулой [1, c. 183–184; 7]:
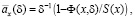(1)
где x – возраст человека, когда начинаются выплаты платежей, δ – интенсивность процентов, S(x) = P(X > x) является функцией выживания случайной величины Х, которая определяет продолжительность его жизни,
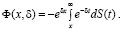(2)
Суть пожизненной ренты состоит в следующем: заключивший договор клиент возраста x перечисляет компании сумму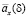 
условных денежных единиц; затем компания будет в течение всей его жизни каждый год платить по одной условной единице денежных сумм. Понятно, что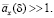 
Рассмотрим задачу оценивания непрерывных пожизненных рент по выборке X1, … Xn продолжительностей жизни индивидуумов [8–10]. Использование классических методов статистической обработки данных часто не позволяет получать адекватные модели, на основе которых строится стратегия развития страховой компанией. При использовании классических параметрических оценок и моделей требуется информация об изучаемом явлении c точностью до неизвестных параметров. На практике часто возникают проблемы с выбором подходящих параметрических оценок и моделей. Обработка данных с привлечением методов непараметрической статистики позволяет синтезировать простые и адекватные (с известными статистическими свойствами) оценки и модели в условиях, когда информация об изучаемом явлении носит общий характер [11].
В статье исследуются свойства непараметрических оценок пожизненной ренты (1), построенных по модельным и реальным данным продолжительностей жизни индивидуумов. Модельные данные генерируются согласно распределению Мэйкхама. Показывается, что эмпирические среднеквадратические ошибки (СКО) оценок, построенных по выборкам из распределения Мэйкхама, а также по выборкам реальных данных, убывают с ростом объемов наблюдений. Таким образом, качество оценивания улучшается с ростом объемов выборок.
Отметим, что полученные результаты оценивания ренты (1) распространяются на общий случай функционалов рент, описывающих, в частности, и новые виды страховых услуг [12, с. 52–63; 13].
Целью работы является исследование свойств непараметрических оценок пожизненной ренты по модельным и реальным данным продолжительностей жизни жителей одного из районов Томской области.
Проведем синтез оценки ренты (1). Сначала оценим S(x) в формуле (1) эмпирической функцией выживания
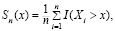(3)
где X1, … Xn – случайная выборка продолжительностей жизни индивидуумов, I(Xi > x) – индикатор события Xi > x, n – объем выборки. Как известно, эмпирическая функция выживания является непараметрической оценкой.
Подставив Sn(x) (3) в функционал (2), имеем
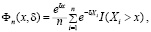
откуда согласно формуле (1) в качестве непараметрической оценки ренты получаем
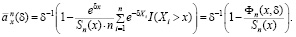(4)
Качество оценки пожизненной ренты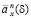 
(4) будем характеризовать ее СКО:
.
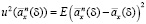Теорема [7]. Если функция выживания S(x) непрерывна, S(x) > 0, то СКО оценки (4)
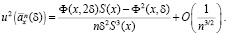
При моделировании рент ограничимся законом Мэйкхама, который для малых возрастов учитывает смертность от несчастных случаев, причем с увеличением возраста влияние несчастных случаев на смертность ослабевает [13–15].
Материалы и методы исследования
Итак, перейдем к оцениванию ренты по статистическим данным, полученным методом исключения для распределения Мэйкхама, которое определяется тремя параметрами A, B, α, для которой функция выживания [13–15]
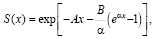
а пожизненная рента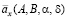 
согласно формуле (1) принимает вид
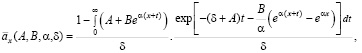(5)
где параметр А учитывает влияние несчастных случаев на смертность, а величина Beαx – влияние возраста на смертность.
Интегралы в (5) вычисляются приближенно методом трапеций при δ = 0,1, A = 0,0007, B = 0,00005, α = 0,092. Приведем на рис. 1 график соответствующей плотности вероятности Мэйкхама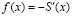 
.
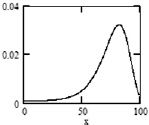
Рис. 1. Плотность вероятности Мэйкхама при A = 0,0007, B = 0,00005, α = 0,092
В табл. 1 приводятся теоретические значения рент, вычисленные по формуле (5).
Таблица 1
Величины рент (5) для различных возрастов x при A = 0,0007, B = 0,00005, α = 0,092, δ = 0,1
|
x лет |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
|
|
9,87 |
9,79 |
9,64 |
9,32 |
8,74 |
7,76 |
6,31 |
4,54 |
2,81 |
Зависимости рент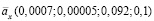 
(5) и их оценок (4)
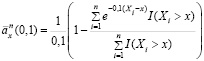(6)
от возраста х для n = 50,100,500 из распределения Мэйкхама представлены на рис. 2.
Теперь рассмотрим оценивание ренты по реальным данным. В одном из районов Томской области было зарегистрировано 410 смертей (2001 г.), на основании чего была получена исходная выборка продолжительностей жизни объема n = 410. Построены непараметрические оценки (6) ренты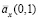 
по всей исходной выборке, а также по случайным выборкам объема 50, 100, 250, которые состоят из элементов исходной выборки. Оценку ренты 
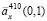, построенную по всей выборке, назовем эталонной оценкой.
Оценки рент (6) для n = 50, 100, 250, 410 и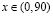 
представлены на рис. 3.
1) 
2) 
3) 
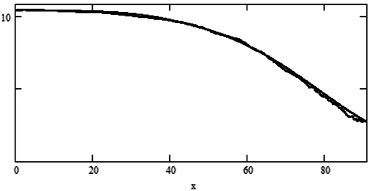
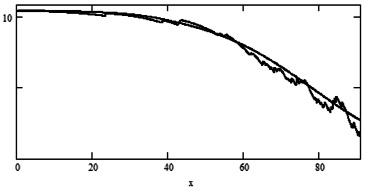
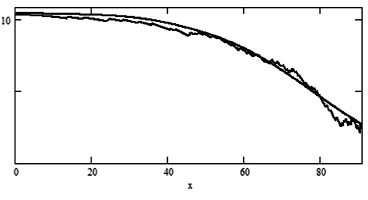
Рис. 2. Зависимость ренты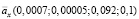 
(гладкая функция) и ее оценки 
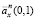(пилообразные функции) от возраста х при n: 1) 50; 2) 100; 3) 500
1) 
2)
3) 
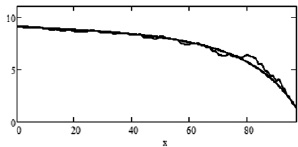
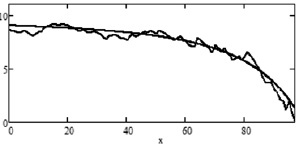
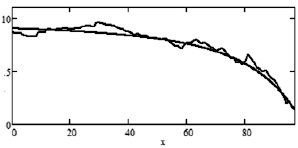
Рис. 3. Эталонные оценки ренты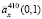 
(6) (гладкая функция) и оценки 
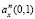(6) (пилообразные функции) для n: 1) 50; 2) 100; 3) 250
Результаты исследования и их обсуждение
Из рис. 2 следует, что модули разностей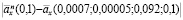 
между оценками рент 
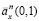и истинной рентой 
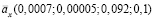с ростом n стремятся к нулю для каждого 
.
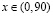Критерием качества оценок (6) может служить эмпирическая СКО
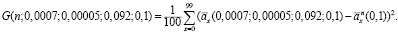(7)
В табл. 2 приводятся для различных n значения эмпирических СКО (7).
Таблица 2
Значения эмпирических СКО (7) для оценок рент (6) при различных n
|
N |
50 |
100 |
250 |
500 |
|
|
0,0475 |
0,00591 |
0,00062 |
0,00093 |
Видим, что согласно табл. 2 качество оценивания улучшается с ростом n.
Аналогичные выводы справедливы и при использовании оценок рент по реальным данным. Из рис. 3 следует, что модули разностей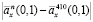 
между оценками рент 
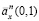и эталонной рентой 
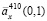с ростом n стремятся к нулю для каждого 
.
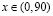Критерием качества оценок (6), построенных по реальным выборкам объема n = 50, 100, 250 относительно эталонной ренты, возьмем
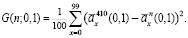(8)
В табл. 3 приводятся значения эмпирических СКО (8) для n = 50, 100, 250.
Таблица 3
Значения эмпирических СКО (8) для оценок рент (6) при различных n
|
n |
50 |
100 |
250 |
|
G(n) |
0,456 |
0,247 |
0,104 |
Согласно табл. 3 качество оценивания также улучшается с ростом n.
Заключение
В статье изучаются свойства оценок пожизненных рент, построенных по модельным и реальным данным. Модельные данные генерируются методом исключения согласно распределению Мэйкхама, которое широко используется на практике. Показывается, что эмпирические СКО оценок, построенных по выборкам из распределения Мэйкхама (7) и по выборкам реальных данных (8), уменьшаются с ростом объемов выборок. Это подтверждает состоятельность оценок согласно утверждению теоремы о СКО оценки ренты (4).