Введение
Визуальные исследования поверхности дна являются неотъемлемой частью комплексных океанологических изысканий и позволяют решать широкий спектр задач. Они включают изучение структуры и численности донных сообществ, анализ морфологических характеристик донных осадков, а также выявление признаков подводной разгрузки природных газов и флюидов, что имеет особое значение в контексте поиска и оценки месторождений полезных ископаемых. Эти исследования помогают оценить биологическое разнообразие, особенности распространения и функционирования экосистем, а также определить состояние морских биоресурсов и наличие возможных загрязнений.
Для визуализации поверхности дна широко используются буксируемые аппараты, оснащенные высококачественными фото- и видеокамерами, направленными вниз, перпендикулярно движению аппарата [1, 2]. Такая ориентация позволяет проводить точную съемку донного рельефа, обеспечивая оптимальное качество изображения и минимизируя влияние мутности воды и прочих помех. Получаемые таким образом фото- и видеоизображения представляют собой своеобразный аналог аэросъемки, но со значительно меньшим охватом площади. Это обеспечивает возможность детального анализа локальных участков дна и дает важную информацию о мелкомасштабных особенностях морфологии и распределения живых организмов.
Для детального анализа подводных видеозаписей выполняется параметризация полученных изображений: производятся подсчет площади поверхности дна, видимой в кадре, а также измерения отдельных участков грунта, природных или техногенных объектов. Одним из самых распространенных методов измерения является применение лазерной масштабной линейки: на поверхность дна с помощью системы параллельных лазерных указателей проецируются яркие отметки, расположенные на известном расстоянии друг от друга (в простейшем случае это две отметки). Данный способ измерения прост в реализации на аппаратном и программном уровне, однако его применение возможно лишь с том случае, если рассматриваемый участок дна достаточно ровный. В этом случае участок дна можно условно считать плоским, что сводит процедуру измерения к сравнению размеров интересующих участков дна с расстоянием между лазерными отметками. Чем более выражены неровности рельефа, тем более выраженной становится погрешность, связанная с несоответствием реальной формы микрорельефа идеальной плоскости. В работах, посвященных измерениям объектов на поверхности дна [3, 4], ровность дна оценивается визуально, без применения каких-либо строгих критериев.
Целями исследования являются оценка влияния перепадов донного микрорельефа на погрешность измерений и определение критериев применимости метода измерений с использованием лазерной масштабной линейки.
Материалы и методы исследования
Для оценки погрешности измерений используется камера, находящаяся на высоте H над плоскостью дна, при этом плоскость изображения камеры параллельна плоскости дна. В таких условиях проекция любого отрезка на изображении будет параллельна исходному отрезку на дне. Это упрощает задачу, сводя ее к одномерному случаю, при котором анализируется сечение сцены, параллельное исследуемому отрезку (рис. 1).
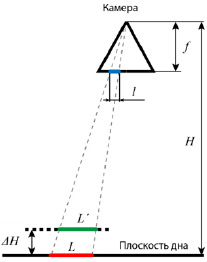
Рис.1. Схема расположения камеры относительно дна для оценки погрешности измерений: f – фокусное расстояние камеры; H – расстояние от принципиальной точки до идеальной плоскости дна; ∆H – изменение высоты грунта в окрестности измеряемого объекта; L – отрезок, лежащий на плоскости дна; L’– отрезок, лежащий параллельно плоскости дна на расстоянии ∆H; l – отрезок на плоскости изображения, являющийся одновременно проекцией отрезков L и L’
Предположим, что на плоскости дна задан отрезок длиной L и его проекция на изображении соответствует отрезку длиной l. Если этот отрезок с длиной L фактически расположен не на плоскости дна, а на некотором расстоянии ∆H выше или ниже ее, но при этом его проекция l остается неизменной, то его реальная длина будет равна L′. Для упрощения расчетов примем, что изменяется лишь расстояние от камеры до измеряемого отрезка, в то время как сами отрезки остаются параллельными плоскости изображения. Относительная погрешность δ в таком случае будет выражаться через отношение разности (L – L’) к L. Из подобия треугольников можно записать это как:
δ = ∆H / Н.
Рис. 2. Фрагменты поверхности дна, использованные для построения 3D-моделей в целях проверки достоверности модели плоского дна. В верхнем углу каждого изображения указан номер станции, на которой получено изображение
На основе вышеописанных рассуждений было проведено исследование относительной погрешности измерений для различных участков поверхности дна. Исследование основывалось на видеоматериалах, полученных буксируемым подводным аппаратом «Видеомодуль», разработанным Институтом океанологии им. П.П. Ширшова РАН [5]. Были использованы данные из нескольких экспедиций НИС «Академик Мстислав Келдыш». Видеозапись велась в ходе буксировки аппарата на расстоянии 1–2 м над грунтом со скоростью 0,5 узла. Для обработки данных использовалось программное обеспечение Agisoft Metashape, с помощью которого были построены плотные трехмерные облака точек для отдельных фрагментов поверхности дна. Эти фрагменты выбирались таким образом, чтобы были представлены разнообразные структуры и формы микрорельефа, но при этом визуально участок дна выглядел ровным. Изображения выбранных фрагментов поверхности дна представлены на рисунке 2.
Каждая 3D-модель масштабировалась в реальных размерах с учетом известного расстояния между лазерными указателями, составляющего 200 мм. После этого сохранялись отдельные файлы с облаком точек 3D-модели и облаком точек, отражающих положения камеры, использованных для реконструкции сцены. Восстановленная 3D-модель была довольно шумной, поэтому перед дальнейшей обработкой к облакам точек применяли сглаживание с использованием фильтра Гаусса. Для каждого облака точек была определена аппроксимирующая плоскость, на которой располагаются все точки, что сводится к решению системы линейных уравнений:
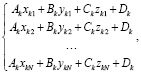
где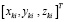 
– i-я точка k-го облака точек, Ak, Bk, Ck, Dk – искомые коэффициенты аппроксимирующей плоскости для k-го облака точек. Поскольку в каждом облаке число точек N >> 3, система уравнений является переопределенной, и ее можно решить методом наименьших квадратов. В результате были получены коэффициенты плоскости дна для каждой станции. Тогда, зная положения всех точек и камер, можно рассчитать расстояния от них до плоскости дна по формуле:
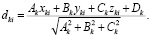
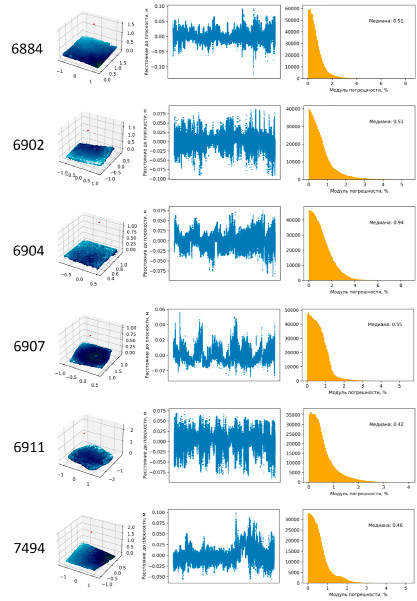
Рис. 3. Результаты исследования зависимости погрешности измерений от изменений микрорельефа поверхности дна и высоты камеры аппарата над грунтом для 6 станций: левый график – трехмерный вид облака точек фрагмента поверхности дна; средний график – удаление точек поверхности дна от аппроксимирующей плоскости; правый график – распределение модуля относительной погрешности. Для каждого распределения приведено медианное значение
Рис. 4. Оценка разброса относительной погрешности измерений сцены с крупными объектами: слева – облако точек, в центре – удаление точек поверхности дна от аппроксимирующей плоскости, справа – распределение модуля относительной погрешности
По аналогичной формуле были рассчитаны расстояния Dk от камеры до плоскости дна. На этом этапе ориентация камер игнорируется, и все они считаются перпендикулярными плоскости дна. Считая каждое значение dki локальным отклонением поверхности дна от идеальной плоскости, получили выражение для относительной погрешности измерений в данной точке при данном расстоянии от камеры до плоскости:
δ = dki / Dk..
Результаты исследования и их обсуждение
Результаты проведенных исследований представлены на рисунке 3. Для каждой из сцен приведены графики значений показателя dki (средний столбец) и распределение модуля относительной погрешности измерений (правый столбец). Высота расположения аппарата над грунтом варьировалась в пределах от 1 до 2 м. Из графиков следует, что отклонения точек от усредненной плоскости составляют не более 100 мм, что соответствует 5–10% от высоты аппарата. Это свидетельствует о том, что с увеличением высоты над поверхностью грунта наблюдается снижение погрешности. Медианное значение модуля относительной погрешности для представленных фрагментов находится в пределах 0,5%, что является достаточно малым и подтверждает высокую точность проводимых измерений при условии, что поверхность дна принимается за идеальную плоскость. Большинство значений погрешности не превышают 2%.
Для проведения сравнительного анализа был изучен участок поверхности дна с крупным камнем. Высота камеры над грунтом в данном случае составляет 1,6 м. На рисунке 4 приведены графики отклонений точек от аппроксимирующей плоскости, а также распределение относительной погрешности измерений. Из графиков видно, что в данном случае погрешность может достигать 10% и более, что является неприемлемо высокой величиной для точных измерений. Медианное значение относительной погрешности для этого участка составляет 3,4%, что почти в 7 раз превышает медианное значение модуля погрешности для ровных участков дна. Эти результаты свидетельствуют о значительном ухудшении точности измерений на участках с неоднородной поверхностью, где наличие крупных объектов, таких как камни, приводит к увеличению погрешности и снижению достоверности аппроксимации.
Заключение
Анализ измерений объектов при аппроксимации поверхности дна плоскостью показывает, что такой подход обеспечивает надежные результаты при условии, что рельеф дна относительно ровный, без резких перепадов, и в кадре отсутствуют объекты высотой более 100 мм. В таких условиях, когда камера установлена на высоте 1–2 м над грунтом, аппроксимация дна плоскостью позволяет получить достоверные измерения. Присутствие на дне более высоких объектов можно легко выявить при просмотре видеозаписей. Кадры, содержащие такие объекты или резкие изменения рельефа, могут быть либо исключены из дальнейшего анализа либо обработаны с помощью методов трехмерной реконструкции, что обеспечивает более точное моделирование сложных участков дна. Таким образом, использование плоскостной аппроксимации является оправданным и эффективным подходом в условиях стабильного рельефа, тогда как для участков с выраженными высотными изменениями необходимо применять методы, учитывающие трехмерные особенности поверхности.
Автор выражает благодарность своему научному руководителю Н.А. Римскому-Корсакову, а также всему коллективу лаборатории гидролокации дна ИО РАН.