Введение
В [1] исследуется, как электрические поля влияют на скорость и механизм кристаллизации в водных растворах. Авторы используют экспериментальные данные и численные модели для демонстрации значительного ускорения кристаллизации при определенных условиях электрического поля. В работе [2] рассматривается влияние примесей на процессы электрокристаллизации. Авторы показывают, что наличие различных ионов может значительно изменять морфологию кристаллов и их свойства, что имеет важные последствия для материаловедения. В [3] изучены влияния электрического поля на рост кристаллов в загрязненной воде. Они проводят эксперименты с различными концентрациями примесей и фиксируют изменения в структуре и размерах кристаллов, что может быть полезно для очистки воды. Работа [4] исследует двойной электрический слой и его роль в кристаллизации. Авторы обсуждают теоретические аспекты взаимодействия между частицами и электрическими полями, что помогает понять механизмы кристаллизации в ионных растворах. В статье [5] рассматривается зависимость скорости кристаллизации от силы электрического поля. Авторы используют кинетические модели для описания процессов и делают выводы об оптимальных условиях для ускорения кристаллизации. Статья [6] предлагает молекулярный взгляд на динамику кристаллизации под воздействием электрических полей. Авторы используют молекулярно-динамическое моделирование для анализа взаимодействий на уровне атомов, что позволяет глубже понять механизмы, лежащие в основе кристаллизации. На основе анализа научных статей можно сделать следующие общие выводы:
− Все статьи подчеркивают значительное влияние электрических полей на процессы кристаллизации, что может быть использовано для управления свойствами материалов.
− Примеси играют ключевую роль в изменении динамики кристаллизации, что важно для разработки технологий очистки и синтеза новых материалов.
− Комбинация экспериментальных и теоретических подходов позволяет получить более полное представление о процессах кристаллизации.
Исходя из анализа научных статей последних лет, целью данной научной работы является исследование влияния электрического поля на динамику кристаллизации в двойном электрическом слое (ДЭС) водных растворов с примесями, комбинируя теоретические и экспериментальные подходы к настоящему исследованию.
Как известно [7, с. 68–70; 8, с. 57–60], функция Лагранжа описывает взаимодействие электрического поля с молекулами воды с примесями. Для вывода уравнения движения молекул воды с примесями в электрическом поле, рассмотрим систему с учетом функции Лагранжа. Предположим, что молекулы воды ориентируются вдоль электрического поля из-за их дипольного момента.
Постановка задачи
1. Двойной электрический слой: ДЭС состоит из слоя адсорбированных ионов на поверхности анода и противоположно заряженных ионов в растворе. В данном случае ДЭС можно рассматривать как два слоя заряда: один у поверхности анода и другой в растворе.
2. Энергия взаимодействия между ионами и молекулами примесей: Ионы и примеси взаимодействуют друг с другом и с электрическим полем, создавая условия для агрегации.
3. Кинетическая энергия: Ионы и молекулы примесей обладают кинетической энергией из-за теплового движения.
В такой постановке задачи функция Лагранжа должна учитывать кинетическую энергию, электростатическую энергию, а также потенциальную энергию взаимодействия ионов и молекул примесей:
Кинетическая энергия T:
Т = ∑ (1/2)mivi2, (1)
где mi – масса i-го иона или молекулы, а vi – его скорость.
Потенциальная энергия электрического поля U: Электрическое поле E между анодом и катодом создает потенциальную энергию для ионов и молекул примесей:
U = ∑qiϕ(xi), (2)
где qi – заряд i-го иона или молекулы, а ϕ(xi) – электрический потенциал в точке xi В ДЭС электрический потенциал ϕ(x) изменяется вблизи анода, создавая зону накопления зарядов и агрегации.
Энергия агрегации W: Агрегация ионов и молекул примесей в ДЭС может быть описана потенциальной энергией взаимодействия, зависящей от расстояния между частицами. Предположим, что взаимодействие можно представить в виде суммы кулоновского взаимодействия и короткодействующего потенциала агрегации, Vagg(rij) между частицами i и j:
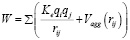, (3)
где ke – электростатическая постоянная, rij – расстояние между частицами i и j, а Vagg(rij) описывает энергию притяжения между частицами на коротких расстояниях, что способствует агрегации в ДЭС.
Таким образом, функция Лагранжа для рассматриваемой системы может быть записана в виде
L = T – U − W. (4)
Подставляя формулы (1)–(3) в (4), получим выражение для функции Лагранжа:
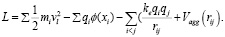(5)
Функция Лагранжа (5) описывает динамику ионов и примесей в электродинамической системе, где электрическое поле между электродами, а также агрегационные силы в ДЭС влияют на движение ионов и их взаимодействие. В результате можно использовать уравнения Лагранжа для получения уравнений движения, которые покажут, как заряженные частицы перемещаются, поляризуются и агломерируются под воздействием электрического поля и сил агрегации. Данная модель поможет проанализировать механизмы накопления ионов в ДЭС и их влияние на общую структуру и динамику системы.
Рассмотрим уравнение Пуассона для описания распределения электрического потенциала в межэлектродной среде с распределением заряда. В данном случае уравнение Пуассона можно использовать для моделирования потенциала вблизи анода, где находится двойной электрический слой (ДЭС).
Уравнение Пуассона записывается в виде
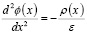, (6)
где ϕ(x) – электрический потенциал; ρ(x) – объемная плотность заряда; ε – диэлектрическая проницаемость воды с примесями.
Для этой задачи введем граничные условия, соответствующие ситуации с ДЭС.
Граничные условия на электродах:
− пусть x = 0 – это анод (находится в точке ϕ = ϕ0);
− пусть x = l – это катод (находится в точке ϕ = 0).
Тогда граничные условия для потенциала:
ϕ(0) = ϕ0 и ϕ(l) = 0.
Плотность заряда ρ(x) в двойном электрическом слое моделируем как быстро убывающую функцию от x, например экспоненциальную функцию, которая описывает распределение ионов:
ρ(x)=ρ0е(–х/λ), (7)
где ρ0 – максимальная плотность заряда у поверхности анода, а λ – характеристическая длина слоя (например, дебаевская длина).
Подставляя функцию (7) для ρ(x) в уравнение Пуассона (6), получим
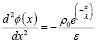. (8)
Решение уравнения Пуассона
Решим уравнение (8) методом интегрирования:
Интегрируем по x и определим dϕ / dx:
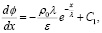(9)
где C1 – константа интегрирования.
Интегрируем второй раз по x, чтобы найти ϕ(x):
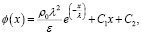(10)
где C2 – еще одна константа интегрирования.
Теперь для нахождения C1 и C2 используем граничные условия, а именно:
при x = 0, ϕ(0) = ϕ0, тогда имеем
.
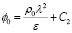Из полученного равенства найдем C2:
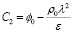. (11)
При x = l ϕ(l) = 0 из уравнения (10) получим
.
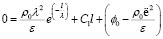Решив это уравнение относительно C1, имеем
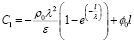. (12)
Подставив (11) и (12) в (10), окончательно получим
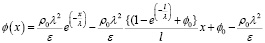. (13)
Решение (13) описывает распределение электрического потенциала ϕ(x) в пространстве между анодом и катодом с учетом образования двойного электрического слоя в окрестности анода. Функция экспоненциального затухания е(–х/λ) описывает влияние плотности заряда вблизи анода, а линейная зависимость от x обусловлена градиентом потенциала между электродами.
Динамика процессов внутри двойного электрического слоя (ДЭС) в окрестности анода является сложным процессом взаимодействия между электрическим полем, ионной концентрацией и переносом вещества.
Рассмотрим основные стадии и механизмы, которые влияют на формирование и поведение ДЭС:
1. Формирование двойного электрического слоя
Двойной электрический слой состоит из двух зон:
− Слой адсорбированных ионов на поверхности анода, которые обладают противоположным зарядом относительно электрода (прямая контактная область).
− Диффузионный слой – область распределения противоположно заряженных ионов в электролите, которая простирается на некоторое расстояние от электрода. Этот слой часто описывается как Гельмгольцевский двойной слой и диффузионный слой Гуи – Чепмена.
При подаче напряжения на анод ионы противоположного заряда притягиваются к его поверхности, формируя компактный слой (в первую очередь из-за электростатического притяжения). Противоположные по заряду ионы в электролите образуют диффузный слой вокруг анода, который компенсирует заряд анода, создавая зону электрического равновесия.
2. Электростатическое взаимодействие и ионная концентрация
Внутри ДЭС создается градиент электрического потенциала. Потенциал резко убывает в контактном слое, а затем медленно уменьшается в диффузионном слое.
Из-за электростатического притяжения концентрация ионов противоположного заряда значительно возрастает вблизи анода. При этом концентрация ионов с тем же знаком, что и анод, уменьшается из-за отталкивания. Это создает локальный дисбаланс ионной концентрации внутри ДЭС.
Под действием электрического поля положительно заряженные ионы движутся к катоду, а отрицательные – к аноду, но вблизи анода их скорость движения замедляется из-за увеличенной концентрации ионов противоположного заряда.
Концентрационный градиент в ДЭС также вызывает диффузию ионов, стремящихся выровнять свою концентрацию. Диффузионный поток направлен от области высокой концентрации (у поверхности анода) к области с меньшей концентрацией (вглубь раствора).
Хотя в идеальном случае конвекция мала в пределах ДЭС, реальные эффекты, такие как тепловая конвекция из-за нагрева, могут оказывать влияние. Конвекция может усилить перенос массы и заряда в пределах слоя.
3. Агрегация ионов и молекул в ДЭС
Ионы противоположного знака, находящиеся вблизи поверхности анода, могут притягиваться друг к другу и образовывать агрегаты, особенно при высокой концентрации ионов. Агрегация ионов усиливается из-за ограниченного объема в ДЭС и сильного электрического поля.
В зависимости от состава раствора и присутствия хлоридов или других примесей ионы анода могут взаимодействовать с другими ионами, образуя нерастворимые соединения. Например, ионы меди и серебра (эксперименты проводили с электродами из меди и серебра) могут образовывать осадки с хлоридами. Эти осадки часто остаются в пределах ДЭС, поскольку они осаждаются на поверхности анода.
В условиях постоянного напряжения ДЭС достигает стационарного состояния, в котором происходит баланс между притоком новых ионов, миграцией, диффузией и осаждением агрегатов.
В стационарном состоянии поток положительных ионов из раствора к аноду компенсируется осаждением ионов или их реакцией на поверхности анода. Это приводит к поддержанию постоянной концентрации заряда в слое, несмотря на постоянный обмен частиц с раствором.
Материалы и методы исследования
Экспериментальная часть
В качестве среды использовалась питьевая вода, содержащая ионы: HCO₃⁻, SO₄²⁻, Cl⁻, Ca²⁺, Mg²⁺. Концентрация SO₄²⁻ составляла 50 мг/л. Для создания электрического поля использовались медные электроды (10 см × 2 см).
Массовое количество осажденного CuSO₄·5H₂O от E и d
|
№ |
Напряжение, U, В |
Напряженность электрического поля Е, В/см |
Расстояние, d (см) |
Масса CuSO₄·5H₂O (г) |
|
1. |
23,5 |
11,76 |
2,0 |
0,88 |
|
2. |
24,5 |
6,13 |
4,0 |
0,66 |
|
3. |
25,5 |
4,25 |
6,0 |
0,48 |
|
3. |
26,5 |
3,31 |
8,0 |
0,39 |
|
4. |
27,5 |
3,06 |
9,0 |
0,32 |
|
5. |
29,0 |
2,90 |
10,0 |
0,29 |
Результаты исследования и их обсуждение
На электроды подавалось напряжение от 1 до 27 В. Расстояние между электродами изменялось в пределах 1–5 см. Измерения напряжения проводились на основе стандартного потенциометрического метода. Масса образовавшегося CuSO₄•5H₂O определялась гравиметрическим методом, а состав полученного вещества – рентгенофазовым анализом (РФА). Количество осажденного медного купороса, полученное в экспериментах, наглядно представлено в таблице.
Из таблицы видно, что масса осажденного вещества (CuSO₄•5H₂O) меняется в зависимости от напряжения, силы электрического поля и расстояния между электродами. Самое большое количество осажденного CuSO₄•5H₂O (0,88 г) получается при максимальной величине электрического поля (11,76 В/см). Это подтверждает, что увеличение силы поля помогает лучше осаждать вещество. Также есть прямая связь: чем выше сила электрического поля, тем больше масса осажденного вещества. Когда расстояние между электродами с 2,0 до 10,0 см, увеличивается снижение массы осажденного вещества. Это может быть связано с тем, что при большем расстоянии сила, действующая на ионы, уменьшается, что затрудняет их осаждение. Таким образом наблюдается прямая зависимость между напряженностью электрического поля и массой осажденного CuSO₄•5H₂O: чем выше напряженность, тем больше масса осажденного вещества, а увеличение расстояния между электродами приводит к уменьшению массы осажденного вещества, что указывает на обратную зависимость, то есть при увеличении напряженности электрического поля масса осажденного вещества будет расти, в то время как увеличение расстояния между электродами может снижать эту массу [4].
Выводы
1. Рассматриваемый процесс отличается от известных кристаллизационных и электрохимических процессов тем, что кристаллизация происходит исключительно в узкой зоне ДЭС, где высокая концентрация ионов и мощное электрическое поле создают уникальные условия для немедленного осаждения микрокристаллов. Процесс кристаллизации вблизи анода зависит от электрического поля и происходит с высокой скоростью при стабильных условиях концентрации, удерживая микрокристаллы в пределах ДЭС, что нехарактерно для обычных условий.
2. Уникальной чертой этого процесса является его локализованность, значительное влияние электрического поля и тесная связь с динамикой ДЭС, что делает его отличным от традиционных электрохимических и кристаллизационных процессов.