Введение
25 июля 2024 г. команда Research компании Google DeepMind, занимающаяся разработкой и применением методов машинного обучения для решения математических задач, объявила о том, что их последние модели AlphaProof и AlphaGeometry 2 смогли решить задания сложнейшей международной математической олимпиады (65th International Mathematical Olympiad, IMO 2024) на уровне серебряного медалиста, отстав от порога для золотой медали на 1 балл [1]. Стоит учесть, что, в отличие от реальных участников олимпиады, решающих задачи 4,5 часа, нейросети справились лишь за 3 дня, но, несмотря на это, в скором времени ожидается многократное ускорение работы AlphaProof. Бурный рост нейронных сетей в самых разных прикладных и фундаментальных областях за последние несколько лет привлекает внимание многих специалистов. Одним из важных вопросов является вопрос эволюции и развития методов обучения.
Цель работы заключается в определении ключевых технических и математических особенностей работы алгоритмов AlphaZero, AlphaProof и похожих моделей, благодаря которым они столь успешно решают математические задачи.
Материалы и методы исследования
Для проведения исследования была осуществлена систематическая оценка и анализ научных публикаций, посвященных эволюции методов машинного обучения с акцентом на разработку и применение моделей, таких как AlphaZero и AlphaProof, в решении математических задач. Основным методом исследования стал литературный обзор, включающий поиск, отбор, классификацию и критический анализ научных статей, опубликованных в период с 2012 по 2024 г. Материалы для анализа были получены из международных научных журналов, включая Nature, IEEE, Science, а также публикаций Google DeepMind. Ключевыми словами поиска стали: AlphaZero, AlphaProof, «машинное обучение», «решение математических задач» «глубокое обучение». Были рассмотрены статьи, охватывающие как технические аспекты алгоритмов, так и их применимость в математике и смежных областях. Критериями отбора статей служили: актуальность исследований в контексте применения методов машинного обучения к математическим задачам, детальное описание архитектур моделей AlphaZero и AlphaProof. Для структурирования данных применялась методология PRISMA, которая позволила систематизировать процесс поиска, исключения дублирующихся данных и анализа релевантных источников.
Результаты исследования и их обсуждение
Все используемые обозначения и символы даны в таблице.
Используемые обозначения
|
p |
вектор, каждая компонента pa которого – это вероятность принять данное положение при данном действии |
|
v |
скаляр оценки результата |
|
Θ |
гиперпараметры нейросети |
|
fΘ |
функция нейросети при данных гиперпараметрах |
|
s |
данное положение на доске (на примере игры в го) |
|
a |
произведенный переход по дереву (действие) |
|
Pr(a|s) |
вероятность занять данное положение на доске при данном действии |
|
z |
скаляр, характеризующий результат игры |
|
πa |
вектор вероятности произвести данный переход по дереву из данного начального положения |
|
vt |
скаляр оценки результата игры на данном шаге |
|
l |
функция потерь в методе градиентного спуска |
|
T |
скаляр, характеризующий конечную позицию на дереве |
|
c |
регулирующий параметр |
|
cpuct |
скаляр, определяющий уровень исследованности данной ветви дерева |
|
x |
параметр ошибки функции потерь, отличающий алгоритм PBT от алгоритма AlphaZero |
Все решения семейства Alpha компании DeepMind, включающие системы AlphaFold 2, AlphaZero, AlphaGo, AlphaStar, AlphaTensor, AlphaCode и др., направлены на решение вычислительных прикладных и научных задач. Рассматриваемая система AlphaProof представляет собой предварительно обученную на большой выборке математических задач и их решений модель с подкреплением AlphaZero, схему работы которой можно проиллюстрировать рис. 1. Более миллиона математических рукописных задач из всех областей геометрии, алгебры, теории вероятностей и теории чисел, математического анализа и других были переведены на формальный язык Lean с помощью Gemini [1]. Это решило большинство проблем с обработкой естественного языка, нейросетевых галлюцинаций и ошибок. Для решения геометрических заданий была значительно улучшена модель AlphaGeometry за счет большего количества задач для обучения.
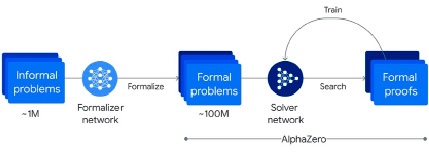
Рис. 1. Схематичное изображение процесса формализации математических задач, обучения и их решения с помощью AlphaZero в системе AlphaProof
AlphaZero – это нейронная сеть, которая обучается за счет соревнования сама с собой в течение многих миллионов попыток с подкреплением. Сначала процесс обучения случаен, но довольно быстро нейросеть учится корректировать свои параметры, причем намного более успешно, чем модели, обученные на заранее подготовленных данных. AlphaZero использует эвристический алгоритм поиска по дереву Монте-Карло (Monte Carlo Tree Search, MCTS) с оценкой НОД функциями на основе deep learning. Именно нейросетевой оценкой НОД этот алгоритм отличается от классического MCTS. Эта нейросеть тренируется предсказывать по прошлым данным дальнейшие данные (SL-policy network), потом тренируется играть сама с собой (RL-policy network), а далее тренируется предсказывать шансы на выигрыш [2]. В основе этого метода все еще лежат математические методы теории принятия решений (марковские процессы принятия решений и их расширения при частичных наблюдениях), теории игр и комбинаторика, метод Монте-Карло и искусственный интеллект в настоящих играх.
Алгоритм MCTS итеративно строит дерево поиска решения до достижения какого-то ограничения по памяти, времени, точности и т.п. Как и у множества других таких алгоритмов, итерации алгоритма производятся в четыре шага: выбор дочерних НОД, расширение количества НОД, моделирование и обновление статистики ошибок [3]. Иллюстрация алгоритма представлена на рис. 2.
Рассмотрим математические основы работы алгоритмов работы AlphaZero. Отметим, что выделенные полужирным начертанием символы – это векторные величины, если не указано иное.
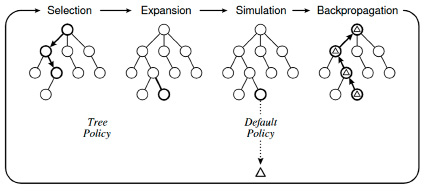
Рис. 2. Схематичное изображение основных шагов алгоритма Monte Carlo Tree Search
Авторы AlphaZero в работе [4] описывают используемую нейросеть с глубоким обучением как функцию (p,v) = fΘ(s) с параметрами Θ. На примере с обучением игры в игру го, нейросеть fΘ(s) принимает данное положение на доске s, а на выходе предоставляет вектор вероятности p с компонентами pa = Pr(a|s) для каждого действия a и скаляр оценки v ожидаемого результата игры z из отношения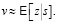 
Параметры Θ подбираются при обучении с играми со случайно подобранными Θ благодаря подкреплению. В каждой игре с начальным положением в ходе поиска по ветви возвращается вектор πa = Pr(a|s0 ). Параметры нейронной сети постоянно обновляются, чтобы минимизировать разницу между величиной предсказанного результата игры vt с реальным результатом z. Для этого параметры Θ корректируются путем градиентного спуска по функции потерь l:
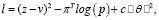(1)
где T – это конечная позиция на дереве, c – параметр, который контролирует регуляризацию этой функции.
В AlphaZero, так же как и в AlphaGo Zero, используется байесовская оптимизация гиперпараметров, но они, как и настройки сети и всего алгоритма, не изменяются от игры в игру [5]. Каждое ребро (s,a) в дереве поиска хранит набор статистических данных:
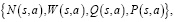(2)
где априорная вероятность P(s,a), количество посещений N(s,a), значение действия Q(s,a), W(s,a) – суммарное значение действия на ветви дерева. Каждое моделирование начинается с начального состояния s0 и итеративно выбирает ходы, которые максимизируют верхнюю доверительную границу вида
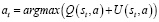, (3)
где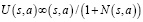 
. В частности, в алгоритме PUCT предлагается такой вид функции U(s,a):
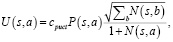(4)
где cpuct – это константа, определяющая уровень исследованности данной ветви.
При прохождении по ребру (s,a) обновляется значение счетчика N(s,a), а Q(s,a) обновляется по правилу
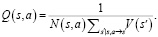(5)
Здесь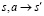 
показывает, что симуляция достигла данного 
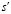при выполнении хода a из состояния s.
Помимо приведенного выше облегченного математического объяснения работы алгоритма работы AlphaZero, полная математическая модель содержит большое количество вероятностных поправок и небольших, но многочисленных шагов корректировок.
После публикации статей AlphaZero несколько исследовательских команд, как в самой компании DeepMind, так и другие, проводили изучение способов и методов оптимизации алгоритмов AlphaZero. Так, исследователи из работы [6] в 2020 г. предложили собственный разработанный «популяционный метод» (PBT). Они использовали подходы, применяемые в машинном обучении для обработки генетических данных, а именно несколько нейросетей со случайными начальными параметрами Θ. Все сети объединяют информацию для улучшения гиперпараметров, а в случае, если они недостаточно точные, то происходит их прямая замена на лучшие гиперпараметры другой нейросети. Также следует отметить, что алгоритм предусматривает возможность ручного изменения гиперпараметров в научно-исследовательских целях.
В данном исследовании использовалось 16 нейросетей для оценок, причем функция потерь теперь также зависит и от параметра ошибки x между z и v:
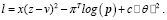(6)
В результате экспериментов авторы обнаружили, что, используя метод PBT к игре в го на поле 19×19, процент побед над другой нейросетью Facebook’s ELF OpenGo v2, которая наиболее близка по мощности со свободными реализациями AlphaZero, составил 74 %. Это говорит о том, что оригинальное применение различных подходов в нейросетевых методах обучения имеет перспективу значительно увеличить способности таких соревновательных систем.
AlphaProof использует заранее обработанные Gemini данные, которые представляют собой формализованные с помощью Lean математические задачи. Это одна из слабых точек технологии и недостаток обучения моделей на естественном языке, из-за чего на настоящий момент невозможно избежать многочисленных искажений. Для решения конкретной математической задачи, AlphaProof необходимо формализовать ее, в соответствии с алгоритмом AlpaZero, описанным выше, генерируются сотни варианты решения этой задачи, а после происходит проверка этого решения с помощью Lean, если оно идентифицируется как неверное, то начинается проверка следующего решения и т.д., до достижения правильного решения. Это возможно благодаря тому, что Lean – это функциональный язык программирования с зависимыми типами на основе CoC (Calculus of Constructions) и CiC (Calculus of Inductive Constructions) [7]. Версия Lean 4 поддерживает высокопроизводительные технологии управления памятью, что может значительно упростить процесс обучения таких сложных систем, как AlpaProof.
На данный момент еще нет публикаций с тестами результатов работы алгоритмов системы AlphaProof, неясно, есть ли отличия точности и скорости ее работы в зависимости от области математики задач, компания Google DeepMind не представила подробные данные о том, какими были промежуточные этапы обучения, о скорости обучения на различных задачах, требовались ли корректировки метода обучения. Эти данные ожидаются в ближайшем будущем с выходом второй версии системы, но уже сейчас становится понятным, что такое использование нейросетей будет большой и важной частью будущего развития математики, так как позволит с высокой точностью и скоростью строго проверять сложнейшие и объемные теоремы, также как и теоремы из областей математики, в которых большое количество абстрактных конструкций и идей – сейчас такие задачи непосильны существующим моделям искусственного интеллекта. Помимо доказательства теорем, это также будет большим прорывом не только для решения сложнейших задач, но и для их составления. О том, как такие нейросети внесут большой вклад в будущее математики на The Oxford Mathematics Public Lectures, рассказал ведущий мировой математик Теренс Тао, который видит в них незаменимый инструмент и роль коллеги при математических исследованиях.
Заключение
Все вышеизложенное позволяет заключить, что значительный прогресс в методах машинного обучения, улучшения и распространения применения AlphaZero в прикладных и фундаментальных исследованиях будет только увеличиваться. AlphaProof, в свою очередь, показывает перспективы в качестве сильного инструмента для ученого, что показывает прогресс в работах по оптимизации и улучшению алгоритмов таких систем.