Введение
Проблема проверки чисел на простоту является фундаментальной в теории чисел и много значит в криптографии. Современные криптографические системы, такие как RSA, основаны на сложности факторизации больших чисел, что требует эффективных и надежных методов определения простоты чисел [1]. На сегодняшний день существует множество алгоритмов проверки простоты, но, несмотря на значительный прогресс в разработке алгоритмов проверки простоты чисел, проблема остается актуальной.
Целью исследования является разработка нового метода тестирования простоты чисел, основанного на анализе симметрии внутри циклов мультипликативной группы по модулю простого числа. В отличие от традиционных методов, данный подход позволяет выявлять структурные закономерности, присущие исключительно простым числам, и исключать составные числа, включая числа Кармайкла, которые являются сложными для обнаружения стандартными вероятностными тестами.
Исследование направлено на выявление ключевых закономерностей в распределении квадратичных вычетов и применение критерия Эйлера для построения нового алгоритма тестирования и проведение экспериментальной проверки разработанного метода на множестве простых и составных чисел.
Материалы и методы исследования
Существуют различные методы тестирования простоты чисел. Решето Эратосфена позволяет эффективно находить простые числа в малых диапазонах, но не подходит для больших значений из-за высокой вычислительной сложности. Алгоритм AKS является детерминированным методом с полиномиальной сложностью, однако требует значительных вычислительных ресурсов. Тест Ферма основан на одноименной теореме, но допускает псевдопростые числа [2]. Тест Миллера – Рабина улучшает метод Ферма за счет разложения числа и вероятностных проверок, но также не гарантирует стопроцентную точность [3]. Тест Соловея – Штрассена использует символ Якоби и дает более надежные результаты, но остается вероятностным [4, с. 140–145]. Эти методы широко применяются в теории чисел и криптографии.
Одной из проблем тестирования простоты является существование псевдопростых чисел, которые могут вводить в заблуждение вероятностные алгоритмы. Псевдопростые числа Ферма – это составные числа, которые удовлетворяют критерию Ферма для некоторых оснований, но не являются простыми. Примеры таких чисел: 561, 1105, 1729, 2465. Они ведут себя как простые относительно теста Ферма, но на самом деле остаются составными. Числа Кармайкла представляют собой особый класс псевдопростых чисел, которые проходят тест Ферма для всех оснований, взаимно простых с ними. Эти числа обходят тест Ферма для практически всех возможных оснований, что делает их сложными для обнаружения с помощью классических вероятностных тестов [5].
Предложенный метод определения основан на анализе особых чисел A и B, связанных между собой по модулю заданного числа p. Числа A и B в каждой паре обладают следующими характеристиками:
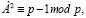
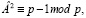
a + b = p.
Данная пара чисел отвечает за формирование значения (–1) в критерии Эйлера для простых чисел вида 1(mod4). Наиболее интересное свойство заключается в том, что пара чисел, дающих (–1) в критерии Эйлера, при умножении дают единицу по остатку p. Это связано с их расположением относительно центральной точки (p–1)/2. Если число А находится на уровне (p–1)/4, то число В расположено на уровне:
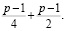
Сумма этих степеней равна (p–1). Согласно теореме Ферма,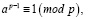 
следовательно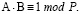 
Простые числа, удовлетворяющие условию p=1(mod4) обладают уникальным свойством: существует ровно одна пара таких чисел. В то же время для простых чисел вида p=3(mod4) такая пара не существует. Это обусловлено тем, что степень t = (p–1)/4, используемая в формировании уровня (p–1)/2, не является целым числом для данного класса. Таким образом, симметричная конструкция чисел A и B, лежащая в основе метода, неприменима к числам этого вида. Для составных чисел, также удовлетворяющих условию p=1(mod4), наблюдается иное поведение. Такие числа могут либо не иметь ни одной пары, удовлетворяющей вышеуказанным условиям, либо содержать более одной такой пары.
Факт существования единственной симметричной и обратимой пары A и B является характерным признаком простоты числа в классе p=1(mod4). Нарушение уникальности или полное отсутствие таких пар однозначно указывает на составной характер числа.
Одним из ключевых элементов предлагаемого теста является работа с квадратичными невычетами по модулю p. В классическом понимании элемент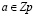 
называется квадратичным невычетом, если сравнение 
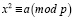не имеет решений при 
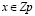[6]. Для корректной работы алгоритма требуется выбрать основание m, обладающее этим свойством. Однако на текущий момент не существует универсального способа определить квадратичный невычет без перебора возможных значений.
В предложенном методе предлагается использовать структурную группировку по остаткам, основанную на известных результатах теории вычетов. Для простых чисел p=1(mod8) значение (p–1)/2 может быть как квадратичным вычетом, так и невычетом. Однако для простых чисел p=5(mod8) значение (p–1)/2 всегда является квадратичным невычетом. Это свойство позволяет существенно упростить выбор основания в рамках метода. В частности, если p=5(mod8), то можно без дополнительной проверки взять основание m = (p–1)/2 так как это значение является квадратичным невычетом. Таким образом, при заданных условиях устраняется необходимость явного перебора, и тест может работать в более оптимальном режиме.
Проверка по одному основанию в симметричном тесте позволяет эффективно исключать все числа, для которых не существует ни одной пары чисел A и B, удовлетворяющей условиям
.
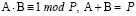Однако такая проверка не является полной, поскольку не гарантирует исключения составных чисел, в которых такие пары все же существуют, но не в единственном экземпляре. Это означает, что, если пара найдена, ее существование еще не доказывает простоту числа, и необходимо убедиться, что она единственная.
Возникновение симметричной пары связано с выбором основания, и такая пара возникает только при использовании основания, напрямую связанного с примитивным корнем по модулю p. Именно примитивные корни обладают свойством порождать всю мультипликативную группу по модулю p, а следовательно, их степень охватывает всю структуру циклов, в которой проявляется симметрия. Таким образом, если основание не связано с примитивным корнем, то пара либо не возникает вовсе, либо может дублироваться при переходе к другим основаниям.
Для исключения ложных положительных результатов необходимо использование второго основания, связанного с другим примитивным корнем или его производной. Если в результате возведения обоих оснований в заданную степень получается одна и та же пара A и B и при этом выполняется условие обратимости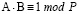 
, то это является свидетельством уникальности пары и, как следствие, сильным подтверждением простоты числа. В противном случае, если различные основания приводят к разным парам или к отсутствию пар, то число составное.
Автор предлагает использовать двойную фильтрацию, которая обеспечивает надежный выбор таких простых чисел, для которых возможно построение пары чисел A и B, обладающих строго определенными симметрическими свойствами. Эта фильтрация основана на двух независимых остаточных условиях: p=5(mod8) и p=1(mod12). Первое из них гарантирует, что значение (p–1)/2 всегда является квадратичным невычетом, а второе – что (p–1) делится на 6. При наложении обоих условий одновременно оказывается, что и (p–1)/6 во всех проверенных случаях также является квадратичным невычетом, а число имеет вид p=13(mod24). Именно это свойство позволяет трактовать основания m1 = (p–1)/2 и m2 = (p–1)/6 как производные от двух примитивных корней, принадлежащих разным подгруппам мультипликативной группы по модулю p. Фильтрация дает нам два «ортогональных» основания, каждое из которых независимо способно проявить симметричную структуру при возведении в степень t = (p–1)/4. Совпадение результатов возведения обоих оснований в степень и получение одной и той же пары А и В свидетельствует о том, что эта пара порождена не случайной подгруппой, а встроена в структуру всей группы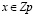 
.
Проверка чисел вида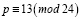 
Рассматривается нечетное натуральное число p, подлежащее проверке на простоту. Тест основан на построении единственной симметричной пары элементов в мультипликативной группе вычетов по модулю p, обладающей структурным свойством:
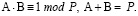
1. Остаточные условия допустимости.
Число p допускается к симметричному тестированию, если выполняется сравнение
.
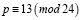Данное условие гарантирует, что значения
t = (p–1)/4, m1 = (p–1)/2, m2 = (p–1)/6
принадлежат множеству целых чисел. Кроме того, при указанном классе по модулю 24 числу p соответствуют значения m1, m2, являющиеся квадратичными невычетами по модулю p.
2. Вычисление образующих элементов.
На основе выбранных оснований вычисляются следующие элементы:
, 
,
, 
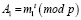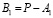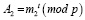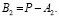
3. Критерий симметричности.
Проверка простоты числа p осуществляется на основании двух условий.
Совпадение пар:
{A1,B1} = {A2,B2}.
Обратимость элементов:
.
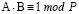4. Результат.
Если оба условия выполняются, число p классифицируется как вероятно простое. В случае нарушения хотя бы одного из условий, число отвергается как составное.
Пример теста
Рассматривается число p = 109. Оно удовлетворяет необходимому остаточному условию: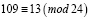 
, поэтому может быть проверено в рамках теста.
Определяются значения:
t = (p–1)/4 = 108/4 = 27,
m1 = (p–1)/2 = 108/2 = 54,
m2 = (p–1)/6 = 108/6 = 18.
Вычисление пар (A, B):
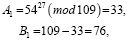
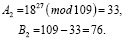
Таким образом,
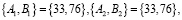
что означает, пары совпадают:
.
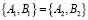Проверка обратимости:
.
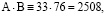
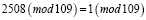Таким образом, выполнено:
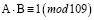
Вывод. Число 109 простое.
Результаты исследования и их обсуждение
С целью оценки эффективности предложенного теста простоты была проведена серия численных экспериментов на множестве натуральных нечетных чисел, удовлетворяющих условию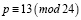 
.
Эксперимент охватывал диапазон от 100 до 106, где общее количество чисел, удовлетворяющих заданному условию, составило 41 663. Из них 9 829 являются простыми, а 7 – составными числами Кармайкла, известными своей способностью имитировать поведение простых чисел в большинстве вероятностных тестов. Для каждого из этих чисел был выполнен симметричный тест, основанный на сравнении двух пар {A1,B1} и {A2,B2}, полученных при возведении двух различных оснований в степень t = (p–1)/4, а также на проверке мультипликативной обратимости элементов пары.
Результаты показали, что все 9 829 простых чисел успешно прошли тест, продемонстрировав уникальную структуру симметрии в группе вычетов по модулю p. При этом ни одно из семи чисел Кармайкла не удовлетворило условиям теста. Таким образом, тест не допустил ни одного ложноположительного результата на данном множестве. Скорость выполнения теста оказалась сопоставимой с тестом Миллера – Рабина. Однако, в отличие от предлагаемого подхода, алгоритм Миллера – Рабина предполагает случайный выбор оснований, а надежность результата напрямую зависит от их количества, которое на практике часто превышает два [7]. Предложенный тест использует фиксированные основания, не зависящие от случайных факторов, и обеспечивает воспроизводимость результата при сохранении вычислительной эффективности.
Заключение
В работе рассмотрен метод тестирования простоты чисел, основанный на анализе симметричных пар, обладающих уникальными обратимыми свойствами в мультипликативной группе вычетов. Метод использует заранее определенную группировку чисел по остаткам, что позволяет выделить подклассы, обладающие структурной симметрией.
Предложенный подход позволяет формировать надежные детерминированные тесты, применимые к определенным классам чисел. За счет наложения условий на вид числа по модулю удается исключить необходимость перебора и обеспечить устойчивую фильтрацию как простых, так и составных чисел. Результаты численного эксперимента подтвердили высокую точность и эффективность метода в пределах выбранного класса.
Одним из направлений дальнейшей работы станет разработка аналогичных тестов для других модульных классов и подгрупп, а также формализация связи между примитивными корнями и симметрией, проявляющейся при возведении оснований в определенные степени. Кроме того, планируется интеграция предложенного метода в состав комплексных алгоритмов первичного тестирования больших чисел, с возможностью его использования в криптографических приложениях.