Введение
В настоящее время сверхкритические технологии широко применяются в процессах адсорбции/десорбции и экстракции веществ из твердой фазы [1, 2]. В этом случае растворитель находится при сверхкритических температуре и давлении. Сильная сжимаемость и высокий коэффициент термического расширения в таком состоянии существенно влияют на тепло- и массообмен и, как следствие, на интенсивность процессов переноса у границы твердого тела и жидкости. В частности, растворимость твердых веществ в сверхкритической среде очень чувствительна к небольшим изменениям температуры и давления вблизи критической точки растворителя [3, 4].
В этой связи при оптимизации процессов адсорбции/десорбции и экстракции важно изучение динамики и теплопереноса в замкнутом объеме бинарной сверхкритической смеси при наличии диффузии одного из компонентов через твердую границу.
Известно, что в замкнутом объеме сверхкритического флюида возмущение температуры на его границе приводит к возникновению так называемого пистон-эффекта, а именно к образованию существенных градиентов температуры и плотности вблизи границы и быстрого изменения во времени почти однородных по пространству плотности и температуры вдали от границы (в «толще среды») [5]. При этом скорость изменения температуры и плотности вдали от границы существенно превышает ту, которая могла бы быть в результате действия механизма теплопроводности, а сам эффект обусловлен высокой сжимаемостью и большим коэффициентом температурного расширения флюида и усиливается по мере приближения к критической точке. В литературе этот эффект получил название поршневого или пистон-эффекта (piston effect) ввиду своего внешнего сходства с откликом замкнутого объема произвольной сжимаемой среды на сжатие поршнем.
Можно предположить, что в случае возмущения концентрации на границе поток массы, обусловленный механизмом диффузии, должен вызвать соответствующий отклик температуры и плотности, похожий на описанный выше эффект. Влияние возмущения концентрации на границе на динамику температурно-плотностной неоднородности изучалось в работе [6]. Авторы предложили назвать такой эффект «массовым пистон-эффектом» (МПЭ) («mass piston effect»). Соответственно, эффект, вызванный возмущением температуры границы замкнутого объема сверхкритического флюида, может быть условно назван «температурным пистон-эффектом» (ТПЭ) («temperature piston effect»).
Цель исследования – изучение особенностей динамики распределений плотности и температуры в замкнутом объеме сверхкритической бинарной смеси при возмущении концентрации одного из компонентов на адиабатической или нагреваемой границе.
Материалы и методы исследования
Исследование проводится методом численного решения системы одномерных безразмерных уравнений для описания движения и теплопереноса в бинарной смеси. Система подробно описана в работе [7] и содержит уравнение движения Навье – Стокса смеси газов (a) и (b), уравнения диффузии для компонентов (а) и (b), уравнение, определяющее плотность смеси как сумму плотностей компонентов (a) и (b), уравнение баланса энергии и уравнение состояния смеси.
Расчеты проводились для одномерной области (рис. 1), заполненной углекислым газом (CO2), компонент (a).
Предполагается, что в начальный момент времени внутри расчетной области среда неподвижна, а плотность, температура и давление равномерно распределены по длине. Плотность равна критической плотности, а температура и давление превышают критические значения для CO2.
Правая граница (x = 1) является адиабатической и непроницаемой.
На левой границе (x = 0) задаются три разных граничных условия:
1. На границе ставится условие непротекания и задается температура выше начальной температуры внутри области.
2. На границе заданы концентрация SF6, компонент (b), и граница считается адиабатической.
3. На границе заданы и концентрация SF6, и температура.
При реализации граничных условий (2) и (3) через границу возникает поток компонента (b) с безразмерной скоростью
,
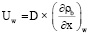где D = D / (ṼL) – безразмерный коэффициент диффузии, D = 5∙10 –8 м2/c – коэффициент диффузии, Ṽ = 49 м/c – масштаб скорости, L = 10-2 м – масштаб длины,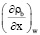 
– текущее расчетное значение градиента безразмерной плотности (массовой концентрации) компонента (b) на границе.
Рис. 1. Схема расчетной области Источник: составлено авторами
Результаты исследования и их обсуждение
На рис. 2 представлен пример распределений безразмерной температуры
T = T / Tкр.SF6
и безразмерной плотности
ρ = ρ / ρкр.SF6
где Tкр.SF6 = 319 K и ρкр.SF6 = 744 кг/м3 – критическая температура и плотность SF6, для граничных условий (1) – пунктирная линия и (2) – сплошная линия к моментам времени 0,5; 1 и 5 с от начала расчета. Прямая горизонтальная сплошная линия соответствует начальному распределению (0 с). Начальная температура превышала критическую Tкр.CO2 = 304,15 K на ΔТ = 0,304 K. Температура границы превышала начальную на δТ = 0,1 K, а значение плотности компонента (b) на стенке составляло ρbw = 0.94∙10–4.
Из рисунка видно, что в случае непроницаемой нагретой стенки (граничное условие (1), штрих-пунктирные линии) вблизи стенки формируется нагретая область (рис. 2, а) и область разрежения (рис. 2, б), а в толще среды температура и плотность однородны и растут с течением времени. Такая картина формирования и дальнейшей эволюции температурно-плотностной неоднородности при нагреве стенки наблюдалась в большом числе экспериментальных и расчетных работ по изучению «температурного пистон-эффекта» в однокомпонентной среде.
В случае возмущения концентрации на адиабатической границе (граничное условие (2), сплошные линии) вблизи границы также формируется нагретая область, и температура в толще среды однородна и растет со временем. Что касается плотности, то в непосредственной близости к границе среда уплотняется, а по мере удаления от границы плотность сначала падает ниже начальной, а затем выходит на некоторую однородную величину, превышающую начальную, которая растет со временем.
В случае граничного условия (3) на левой границе поддерживается заданная температура, превышающая начальную, и заданное значение концентрации компонента (b). При такой постановке распределения температуры и плотности должны формироваться в результате совместного действия температурного и массового пистон-эффекта. В качестве иллюстрации на рис. 3 сплошными линиями представлены результаты расчетов температуры и плотности для концентрации компонента (b) ρbw = 0.94∙10-3 на границе и разных значений температуры δТ. Там же приведено распределение температуры и плотности (пунктирная линия) для того же значения граничной концентрации, но при наличии адиабатической стенки.
Из рисунка видно, что при самом большом значении температуры из этой серии на стенке δТ = 1K распределение температуры (на рис. 3, а, оно не показано, так как лежит значительно выше остальных) и плотности близко к тому, что формируется при отсутствии диффузии с границы. На распределении плотности видна область разрежения около стенки и происходит уплотнение однородной среды вдали от стенки. Профиль температуры лежит значительно выше профиля, формирующегося при отсутствии потока тепла с границы (пунктирная линия), и эта разница обусловлена потоком тепла со стенки. Можно сказать, при таком соотношении температуры и концентрации на стенке доминирует температурный пистон-эффект.
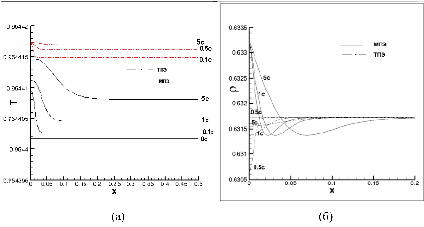
Рис. 2. Пример распределений безразмерной (а) температуры и (б) плотности смеси для граничного условия (1) (штрих-пунктирная линия), «температурный пистон-эффект» (ТПЭ) и для граничного условия (2) (сплошная линия), «массовый пистон-эффект» (МПЭ) Источник: составлено авторами
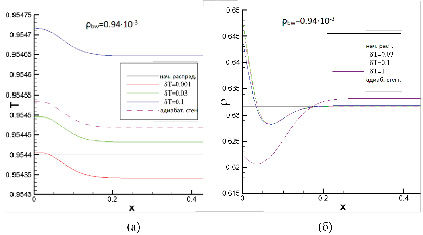
Рис. 3. Распределение (а) температуры и (б) плотности через 5 с после начала расчета для граничного условия (3) при концентрации компонента (b) ρbw = 0.94∙10-3 и различных значениях температуры стенки δТ Источник: составлено авторами
При температуре δТ = 0,1 и 0,03 K профиль плотности близок профилю, характерному для случая отсутствия потока тепла на стенке: вблизи нее образуются области уплотнения и разрежения и происходит подъем плотности в толще среды. Можно сказать, что в этом случае доминирует массовый пистон-эффект. Необходимо отметить, что распределение температуры лежит ниже распределения для нулевого потока тепла со стенки (пунктирная линия). Это говорит о том, что при таком соотношении температуры и концентрации компонента (b) на стенке, вследствие действия массового пистон-эффекта температура среды вблизи нее оказывается выше температуры самой стенки. Поэтому возникает поток тепла от среды в стенку, что приводит к охлаждению толщи среды вследствие действия температурного пистон-эффекта. Более того, при наименьшем значении нагрева δТ = 0,001 K охлаждение оказалось настолько сильным, что температура в толще среды упала ниже начального уровня.
Заключение
На основе системы уравнений для описания движения и теплопереноса в сверхкритической бинарной смеси проведены расчеты динамики температурно-плотностной неоднородности, вызванной возмущением концентрации одного из компонентов на адиабатической или нагреваемой границе области, заполненной сверхкритической смесью углекислого газа и шестифтористой серы. При отсутствии возмущения концентрации на границе подвод тепла со стенки приводит к формированию и эволюции температурно-плотностной неоднородности, характерной для «температурного пистон-эффекта» в однокомпонентной среде. При отсутствии теплового воздействия на границе возмущение концентрации одного из компонентов вызывает характерное изменение температуры и плотности внутри области, которое можно назвать «массовым пистон-эффектом». При возмущении на границе и температуры, и концентрации действуют оба этих эффекта. Проведен анализ различных режимов формирования распределений плотности и температуры в зависимости от соотношения граничной температуры и концентрации одного из компонентов. Показано, что при доминировании массового пистон-эффекта возможны режимы, при которых происходит охлаждение толщи среды.