Введение
Одним из актуальных и перспективных направлений исследований в механике жидкости является изучение динамики гидромеханических систем при периодических по времени воздействиях. Актуальность и перспективность данного научного направления обусловлены наличием у результатов проводимых исследований фундаментального и прикладного содержания, тем, что периодические воздействия способны качественным образом влиять на динамику гидромеханических систем, быть средством управления системами [1], а также возможностью использования получаемых результатов при организации актуальных направленных исследований, при поиске инновационных подходов к решению актуальных научных и технических проблем, в частности проблем аэрокосмической техники, тонкой химии, экологии [2–4]. Состояние исследований в рассматриваемом направлении характеризуется работами [5, 6].
К числу важных современных научно-технических задач с очевидностью относится задача синхронизации движения составных частей механических систем. Отклонения от синхронности могут качественным образом отражаться на динамике систем. В настоящей работе начато изучение вопросов, касающихся синхронизации движения в гидромеханических системах. Поставлена и решена новая задача о движении гидромеханической системы с вязкой жидкостью при периодических воздействиях.
Целью исследования является решение вопроса о возможности синхронизации движения свободной твердой части гидромеханической системы с вязкой жидкостью (часть системы, движение которой не задано, подлежит определению) и твердой части системы, совершающей заданное периодическое движение посредством внешнего периодического силового воздействия на систему (на свободную твердую часть системы).
Постановка и решение задачи
Имеется гидромеханическая система, состоящая из вязкой несжимаемой жидкости и абсолютно твердых тел – стенки η и однородной пластины ξ. Стенка η ограничена плоскостью, перпендикулярной к оси X инерциальной прямоугольной системы координат X, Y, Z, и пересекающей ось X в точке X = 0. Пластина ξ ограничена плоскостями, перпендикулярными к оси X и пересекающими ось X в точках X = A, X = B (A > 0, B > A – постоянные). Жидкость заполняет область Ω : 0 < X < A; – ∞ < Y < ∞; – ∞ < Z < ∞. Стенка η совершает заданное движение со скоростью U = Ue, периодически с периодом T изменяющейся со временем t (e = {0, 1, 0}; U = Ũsin (2πt/T); Ũ > 0 – постоянная). Пластина ξ подвергается силовому воздействию со стороны жидкости и внешнему силовому воздействию, периодически с периодом T изменяющемуся со временем. Вследствие оказываемых силовых воздействий пластина ξ движется со скоростью W = We, которую необходимо найти. Скорость жидкости V и давление в жидкости P не зависят от координат Y, Z. Требуется определить периодическое по времени движение гидромеханической системы (свободных частей гидромеханической системы – жидкости и пластины ξ).
Пусть τ = t / T; x = X / A; ρ – плотность жидкости; ξ' – абсолютно твердое тело, (какая-либо) часть пластины ξ, заполняющая в (какой-либо) момент времени t = t' область A < X < B, Y* < Y< Y* + DY , Z* < Z < Z* + DZ (Y*, Z*, DY > 0, DZ > 0) – постоянные);
ρ' – плотность тела ξ' (пластины ξ);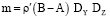 
– масса тела ξ';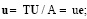 
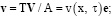
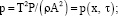
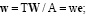ν – кинематический коэффициент вязкости жидкости; 
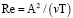– число Рейнольдса; 
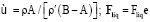– сила, действующая на тело ξ' со стороны жидкости;
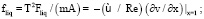
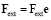– внешняя сила, действующая на тело ξ';
(
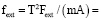
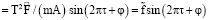
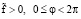– параметры).
Задачу о движении гидромеханической системы составляют уравнение движения пластины ξ (тела ξ' ), уравнение Навье – Стокса и условия на твердых границах жидкости
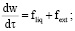(1)
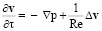в Ω; (2)
v = u при х = 0; (3)
v = w при х = 1. (4)
Из (2)–(4) следует
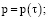(5)
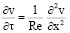в Ω; (6)
v = u при х = 0; (7)
v = w при х = 1. (8)
Сделаем в (6)–(8) подстановку
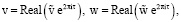(9)
где ṽ – функция x;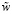 
– постоянная. Используя полученные в результате этого соотношения, определим задачу
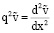для 0< х < 1; (10)
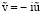при х = 0; (11)
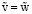при х = 1. (12)
Здесь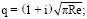 
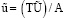. Решая уравнение (10), найдем
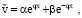(13)
где α, β – постоянные. Из (11)–(13) следует
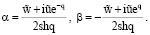(14)
Используя (13), (14) получим
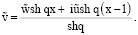(15)
Согласно (1), (9), (15) имеем
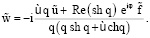(16)
Формулами (5), (9), (15), (16) определяется точное решение задачи (1)–(4).
Обратимся к вопросу о возможности синхронизации движения твердых частей гидромеханической системы посредством внешнего силового воздействия на систему (на свободную твердую часть системы – пластину ξ). Представим комплексную амплитуду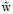 
в виде
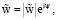(17)
где ψ – аргумент амплитуды
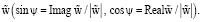
Из (9), (17) следует
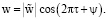(18)
Синхронность движения пластины ξ и стенки η состоит в том, что при любом значении τ имеет место равенство
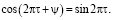
Данное равенство (для любого τ) выполняется тогда и только тогда, когда выполняются соотношения
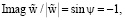
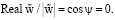(19)
Пусть значения Re велики по сравнению с единицей. Используя (16), получим
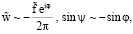
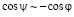при Re → ∞. (20)
Согласно (18)–(20) при больших Re имеет место следующее. Пластина ξ и стенка η движутся синхронно, если «управляющий» параметр φ удовлетворяет условию
φ = π/2 (21)
(если φ ≠ π / 2 синхронность отсутствует). При выполнении (21) синхронное (с движением стенки η) движение пластины ξ происходит со скоростью
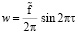
(амплитуда скорости пластины ξ зависит от «управляющего» параметра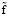 
). Внешнее силовое воздействие, обеспечивающее синхронность движения пластины ξ и стенки η, определяется формулой
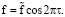
Пусть значения Re ˃ 0 малы по сравнению с единицей. Используя (16), пренебрегая величинами, малыми по сравнению с Re, получим
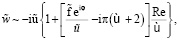
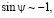
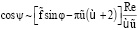при Re→0. (22)
Согласно (18), (19), (22) при малых Re имеет место следующее.
1. В нулевом приближении (при учете только слагаемых, не зависящих от Re) пластина ξ и стенка η движутся синхронно, независимо от того, какова сила fext (независимо от значений параметров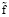 
, φ).
2. В первом приближении (при учете наряду со слагаемыми, не зависящими от Re, также слагаемых, пропорциональных Re) пластина ξ и стенка η движутся синхронно или несинхронно в зависимости от значений «управляющих» параметров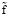 
, φ. При выполнении соотношения 
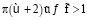синхронность движения невозможна. Для значений «управляющего» параметра 
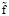, при которых выполняется соотношение 
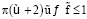, пластина ξ и стенка η движутся синхронно, если «управляющий» параметр φ удовлетворяет условию
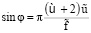(23)
(если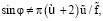 
синхронность отсутствует). При выполнении (23) возможна реализация синхронного (с движением стенки η) движения пластины ξ со следующими скоростями
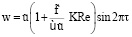для 0 < φ < π/2;
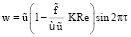для π/2 < φ < π;
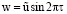для φ = π/2,
где
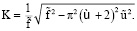
Внешнее силовое воздействие, обеспечивающее синхронность движения пластины ξ и стенки η , определяется формулами
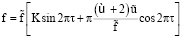
для 0 < φ < π/2;
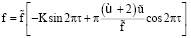
для π/2 < φ < π;
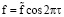для φ = π/2.
Заключение
Рассмотрена новая задача о движении гидромеханической системы с вязкой жидкостью.Найдено точное решение задачи. Установлена возможность осуществления синхронизации периодического движения твердых частей гидромеханической системы посредством внешнего периодического силового воздействия на систему. Обнаружено, что при наличии синхронности движение свободной твердой части системы может происходить с различными скоростями. Полученные результаты могут использоваться, в частности, в исследованиях прикладного характера, касающихся динамики гидромеханических систем.