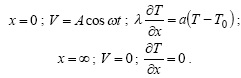В процессе различных операций твердые материалы и их расплавы могут подвергаться вибрационным воздействиям, которые имеют различные частотные спектры и амплитуды и могут действовать в различных направлениях. Комплексное теоретическое исследование процессов, протекающих при вибровоздействии, представляет собой сложную математическую задачу, поэтому целесообразнее рассмотреть различные простые модели, учитывающие основные особенности вибрационного воздействия на вязкопластичные материалы. В частности, рассмотрим разогрев вязкой жидкости при ее контакте с горизонтальной поверхностью, совершающей простое гармоничное колебательное движение с частотой ω . Такое движение поверхности является отдельным элементом вероятного вибрационного воздействия на вещество.
Анализировалась задача в следующей постановке. Вязкая несжимаемая
жидкость занимает полупространство х>0, а плоскость y, z, является
твердой поверхностью. Ось выберем вдоль направления колебаний поверхности.
Скорость колеблющейся поверхности ![]()
Будем предполагать, что вязкость жидкости от температуры зависит экспоненциально
![]()
где Т абсолютная температура; предэкспонент; U энергия активации вязкого течения; R универсальная газовая постоянная.
Экспоненциальный вид зависимости включает в себя как частные случаи рейнольдсову и гиперболическую зависимости и случай постоянной вязкости.
Нестационарную систему уравнений движения и теплового баланса с учетом диссипации энергии можно записать в виде
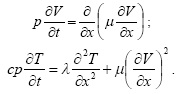
где V скорость жидкости; x Эйлерова координата; t время; λ и c теплопроводность и вязкость; μ динамическая вязкость.В начальный
момент времени температура жидкости равна температуре поверхности. Скорость жидкости на поверхности x=0 должна удовлетворять условию (условие прилипания): V=U.
Будем считать, что через поверхность с окружающей средой осуществляется теплообмен по закону Ньютона. Тогда граничные условия можно записать следующим образом: