В [1] приводится возможный вариант алгоритмизации теории интегрирования элементарнах функций на основе реализуемой на ЭВМ теории абелевых групп. В настоящей работе изучается формализация теории групп без предположения о коммутативности групповой операции, что даёт возможность применить теорию к изучению матричного исчисления И. А. ЛаппоДанилевского [2], которое реализуется с помощью пакетов Derive, Matlab и других. Свободные переменные теории a, b, c, x, ... и другие интерпретируются как матрицы размерности nxn. Соответственно предметные постоянные o и 1 будут интерпретироваться как матрица 0 из нулей и единичная E размерностей n x n . Групповые операции сложения и умножения рассматриваются как матричные. Поскольку по сложению имеет место коммутативность, то теоремы T1 T8 [1] запишутся в виде:
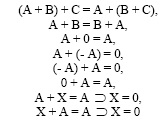
и т.д. Пусть det A обозначает определитель матрицы A, тогда теоремы T1´ - T8´ [1] имеют интерпретации в виде:
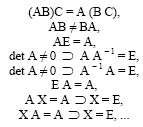
и т.д. Если добавить [1] закон дистрибутивности A (B +C) = A B + A C, аксиомы дифференцирования (A + B)´ = A´ + B´, (AB)´ =A´B +A B´, где A´, B´, (A + B)´ , ... и т.д. здесь штрихом обозначается дифференцирование всех элементов соответствующих матриц по параметру t ; аксиому существования корня квадратного из матрицы X 2 A =0 (матричный аналог частного случая уравнения
Абеля); аксиому существования матрицы экспоненты X = e A t (где A постоянная матрица) в виде X´ = A X ; ... и т. д., то получим матричный аналог теории элементарных функций, реализуемой в системе Matlab, насчитывающей таких функций около трёхсот. Для вычислений e A t задаётся матричным рядом E + (At)/ 1! + (At) 2 / 2! +..... , сходящимся для любых At (аналог скалярной целой функции [2]). Аналогичным образом вычисляются sin A , cos A, sh A, ch A, ... и т.д. Ho cos A и sin A можно вычислить и другим способом, поскольку e iA = cos A + i sin A, то вещественная часть этого равенства даст cos A, а мнимая даст sin A. Берём в качестве примера матрицу A размерности 2 x 2, первая строка которой 1, 2, а вторая строка 3, 4 , что на языке Matlab запишется в виде:
>> A = [ 1 2 ; 3 4 ] ;
Затем для рассматриваемого случая вычисляем e Ai:
>> expm (i * A),
что приводит к ответу
ans = 0.8554 0.4656 i 0.1109 0.1484 i 0.1663 0.2226 i 0.6891 0.6882 i Вычисляя вещественную B = real (ans) и мнимую части C = imag (ans), найдём, что тождество sin 2 A + cos 2 A = E выполняется с точностью до четырёх знаков после запятой.
СПИСОК ЛИТЕРАТУРЫ:
1. Тарушкин В.Т., Тарушкин П.В., Тарушкина Л.Т., Юрков А .В. Элементарная теория групп в системе Deductio. VI общероссийская научная конференция "Перспективы развития вузовской науки", г. Сочи, 21 23 сентября 2009 г. (в печати).
2. Смирнов В.И. Курс высшей математики, т. 3, ч. 2 М .: ГИТТЛ, 1951. 676 c.
3. Дьяконов В. Matlab 6 . M.: ПИТЕР ,2001. 592c.

